Hi, I’m Tejas kamble
a Data Engineer AI Engineer Researcher
I specialize in the dynamic and ever-evolving field of Artificial Intelligence, Data Science. My expertise lies in harnessing the power of AI, Natural Language Processing (NLP), Data Engineering, and cutting-edge AI-ML technologies to unravel complex problems and unlock new possibilities.


About Me
With a passion for creating intelligent systems, I thrive on developing innovative solutions that bridge the gap between raw data and actionable insights. Whether it’s crafting robust algorithms, engineering data pipelines, or delving into the realms of machine learning, I am dedicated to pushing the boundaries of what AI can achieve.
I’ve actively engaged in developing AI-driven applications, collaborating on research initiatives, and contributing to the advancement of the field. My current endeavors include spearheading two significant projects – one focused on exploring the intersection of AI and healthcare, and another involving the development of a platform that seamlessly integrates AI into everyday life.
Certificates and Awards
Education

Computer Engineering
Savitribai Phule University
Pune, Maharashtra ‧ Government

High School
Yashwantrao Chavan College Of Science
Karad 415110, Satara, Maharashtra

Secondary School Education
Adarsh Vidyamandir
Wing, Karad, Maharashtra
Projects and Research

Cloud cost management has evolved from manual spreadsheet tracking to sophisticated AI-driven automation. As organizations increasingly adopt multi-cloud strategies, the complexity of cost optimization grows exponentially. This comprehensive guide explores building agentic AI systems that autonomously manage cloud costs, leveraging open-source models and cutting-edge AI frameworks.
Understanding Agentic AI Systems
Agentic AI systems represent a paradigm shift from traditional reactive AI to proactive, goal-oriented artificial intelligence. Unlike conventional AI models that respond to queries, agentic systems operate autonomously, making decisions and taking actions to achieve specific objectives.
Core Characteristics of Agentic AI
Autonomy: The system operates independently, making decisions without constant human intervention while respecting predefined boundaries and policies.
Goal-Oriented Behavior: Each agent has clear objectives, such as minimizing cloud costs while maintaining performance SLAs, and continuously works toward achieving these goals.
Environmental Awareness: Agents continuously monitor their environment, understanding cloud resource utilization, cost trends, and performance metrics in real-time.
Learning and Adaptation: The system learns from past decisions, improving its cost optimization strategies over time through reinforcement learning and feedback loops.
Multi-Agent Coordination: Different specialized agents collaborate, such as a cost monitoring agent working with a resource optimization agent and a compliance agent.
Architecture of Agentic AI for Cloud Cost Management
Multi-Agent System Design
The architecture consists of specialized agents, each responsible for specific aspects of cloud cost management:
Cost Monitoring Agent: Continuously collects and analyzes billing data from multiple cloud providers, detecting anomalies and trends in real-time.
Resource Optimization Agent: Evaluates resource utilization patterns and makes recommendations or autonomous decisions about rightsizing, scaling, and resource allocation.
Compliance Agent: Ensures all cost optimization actions comply with organizational policies, regulatory requirements, and client-specific constraints.
Forecasting Agent: Uses predictive models to anticipate future costs and resource needs, enabling proactive optimization strategies.
Notification Agent: Manages communication with stakeholders, sending alerts, reports, and recommendations through appropriate channels.
Action Execution Agent: Safely implements approved optimization actions across cloud environments, with rollback capabilities for safety.
Data Flow and Integration Layer
The system integrates with multiple data sources and APIs:
Cloud Provider APIs: Direct integration with AWS Cost Explorer, Azure Cost Management, Google Cloud Billing, and other cloud providers’ cost and usage APIs.
Infrastructure Monitoring: Integration with Prometheus, Grafana, Datadog, or New Relic for real-time performance metrics.
Configuration Management: Connection to Terraform, Ansible, or CloudFormation for infrastructure state management.
Business Systems: Integration with ERP, CRM, and project management systems for cost allocation and chargeback functionality.
Open Source AI Models and Frameworks
Large Language Models Integration
Ollama Integration: Ollama provides local deployment of open-source models, ensuring data privacy and reducing API costs. Key models include:
- Llama 2/3: Excellent for natural language processing tasks, generating cost optimization reports, and explaining complex cost patterns to stakeholders
- Code Llama: Specialized for generating and analyzing infrastructure code, automating Terraform configurations, and creating cost optimization scripts
- Mistral 7B/8x7B: Efficient models for real-time decision making and cost analysis with lower computational requirements
Anthropic Claude Integration: While not open-source, Claude’s API provides sophisticated reasoning capabilities for complex cost optimization scenarios and policy interpretation.
Mistral AI Models: Open-weight models offering excellent performance for cost analysis tasks:
- Mixtral 8x7B: Mixture of experts model providing efficient processing for multi-task cost optimization
- Mistral 7B: Compact model suitable for edge deployment and real-time decision making
Specialized AI Tools and Libraries
Machine Learning Frameworks:
- scikit-learn: For traditional ML tasks like anomaly detection, clustering cost patterns, and regression analysis
- XGBoost/LightGBM: Gradient boosting for accurate cost forecasting and resource usage prediction
- PyTorch/TensorFlow: Deep learning frameworks for complex pattern recognition in cost data
Time Series Analysis:
- Prophet: Facebook’s time series forecasting tool, excellent for predicting cloud costs with seasonal patterns
- ARIMA/SARIMA: Classical time series models for cost trend analysis
- Neural Prophet: Deep learning approach to time series forecasting
Reinforcement Learning:
- Stable Baselines3: Implementation of RL algorithms for autonomous cost optimization decisions
- Ray RLlib: Distributed reinforcement learning for complex multi-agent scenarios
Natural Language Processing:
- Transformers (Hugging Face): Pre-trained models for processing cost reports, policy documents, and generating explanations
- spaCy: Efficient NLP library for text processing and entity extraction from cost documentation
Technical Implementation Stack
Backend Infrastructure
Core Application Framework:
# FastAPI-based microservices architecture
from fastapi import FastAPI, BackgroundTasks
from pydantic import BaseModel
import asyncio
from typing import List, Dict
import httpx
app = FastAPI(title="Agentic Cloud Cost Management")
class CostAgent:
def __init__(self, model_endpoint: str):
self.model_endpoint = model_endpoint
self.client = httpx.AsyncClient()
async def analyze_costs(self, cost_data: Dict):
# Integration with Ollama or other model endpoints
pass
Message Queue and Orchestration:
- Apache Kafka: Real-time data streaming for cost events and optimization triggers
- Celery with Redis: Task queue for asynchronous cost optimization jobs
- Apache Airflow: Workflow orchestration for complex cost management pipelines
Database Architecture:
- InfluxDB: Time-series database for storing cost and usage metrics
- PostgreSQL: Relational database for client configurations, policies, and audit trails
- MongoDB: Document store for unstructured data like cost reports and optimization recommendations
- Redis: Caching layer for frequently accessed cost data and model predictions
AI Model Deployment and Management
Local Model Deployment with Ollama:
# Install and configure Ollama
curl -fsSL https://ollama.ai/install.sh | sh
# Pull required models
ollama pull llama3
ollama pull mistral
ollama pull codellama
# Create custom cost management model
ollama create cost-optimizer -f ./Modelfile
Model Serving Infrastructure:
- TorchServe: Production-ready serving for PyTorch models
- MLflow: Model versioning, experiment tracking, and deployment
- Kubeflow: Kubernetes-native ML workflows
- BentoML: Framework for building AI application APIs
Container Orchestration:
# Kubernetes deployment for AI agents
apiVersion: apps/v1
kind: Deployment
metadata:
name: cost-optimization-agent
spec:
replicas: 3
selector:
matchLabels:
app: cost-agent
template:
metadata:
labels:
app: cost-agent
spec:
containers:
- name: cost-agent
image: cost-optimizer:latest
resources:
requests:
memory: "2Gi"
cpu: "1000m"
limits:
memory: "4Gi"
cpu: "2000m"
Cloud Provider Integration
Multi-Cloud Cost Collection:
import boto3
from azure.mgmt.consumption import ConsumptionManagementClient
from google.cloud import billing
import asyncio
class MultiCloudCostCollector:
def __init__(self):
self.aws_client = boto3.client('ce') # Cost Explorer
self.azure_client = ConsumptionManagementClient(credential, subscription_id)
self.gcp_client = billing.CloudBillingClient()
async def collect_all_costs(self):
tasks = [
self.get_aws_costs(),
self.get_azure_costs(),
self.get_gcp_costs()
]
return await asyncio.gather(*tasks)
Infrastructure as Code Integration:
- Terraform Provider: Custom provider for cost-optimized resource provisioning
- Pulumi: Modern IaC with native programming language support
- CDK (Cloud Development Kit): Define cloud resources using familiar programming languages
Agent Communication and Coordination
Inter-Agent Communication Protocol
Message Passing System:
from dataclasses import dataclass
from enum import Enum
from typing import Any, Dict
class MessageType(Enum):
COST_ALERT = "cost_alert"
OPTIMIZATION_REQUEST = "optimization_request"
ACTION_APPROVAL = "action_approval"
STATUS_UPDATE = "status_update"
@dataclass
class AgentMessage:
sender: str
recipient: str
message_type: MessageType
payload: Dict[str, Any]
timestamp: float
priority: int = 1
class AgentCommunicationHub:
def __init__(self):
self.agents = {}
self.message_queue = asyncio.Queue()
async def route_message(self, message: AgentMessage):
if message.recipient in self.agents:
await self.agents[message.recipient].receive_message(message)
Consensus Mechanisms: Implement voting systems for critical decisions affecting multiple clients or significant cost impacts, ensuring no single agent can make potentially harmful decisions without consensus.
Event-Driven Architecture
Event Streaming with Kafka:
from kafka import KafkaProducer, KafkaConsumer
import json
class CostEventProducer:
def __init__(self):
self.producer = KafkaProducer(
bootstrap_servers=['localhost:9092'],
value_serializer=lambda x: json.dumps(x).encode('utf-8')
)
def emit_cost_event(self, event_type: str, data: Dict):
event = {
'event_type': event_type,
'timestamp': time.time(),
'data': data
}
self.producer.send('cost-events', event)
class OptimizationAgent:
def __init__(self):
self.consumer = KafkaConsumer(
'cost-events',
bootstrap_servers=['localhost:9092'],
auto_offset_reset='latest',
value_deserializer=lambda m: json.loads(m.decode('utf-8'))
)
async def process_events(self):
for message in self.consumer:
await self.handle_cost_event(message.value)
Implementing Intelligent Cost Optimization
Anomaly Detection System
Statistical Anomaly Detection:
import numpy as np
from sklearn.ensemble import IsolationForest
from sklearn.preprocessing import StandardScaler
class CostAnomalyDetector:
def __init__(self):
self.model = IsolationForest(contamination=0.1, random_state=42)
self.scaler = StandardScaler()
self.is_trained = False
def train(self, historical_costs: np.ndarray):
scaled_costs = self.scaler.fit_transform(historical_costs)
self.model.fit(scaled_costs)
self.is_trained = True
def detect_anomalies(self, current_costs: np.ndarray) -> List[bool]:
if not self.is_trained:
raise ValueError("Model must be trained first")
scaled_costs = self.scaler.transform(current_costs)
anomaly_scores = self.model.decision_function(scaled_costs)
return self.model.predict(scaled_costs) == -1
Deep Learning Anomaly Detection:
import torch
import torch.nn as nn
from torch.utils.data import DataLoader, TensorDataset
class CostAutoencoderAnomalyDetector(nn.Module):
def __init__(self, input_dim: int, hidden_dims: List[int]):
super().__init__()
# Encoder
encoder_layers = []
current_dim = input_dim
for hidden_dim in hidden_dims:
encoder_layers.extend([
nn.Linear(current_dim, hidden_dim),
nn.ReLU(),
nn.BatchNorm1d(hidden_dim)
])
current_dim = hidden_dim
# Decoder
decoder_layers = []
for i in range(len(hidden_dims) - 1, -1, -1):
decoder_layers.extend([
nn.Linear(current_dim, hidden_dims[i] if i > 0 else input_dim),
nn.ReLU() if i > 0 else nn.Sigmoid()
])
current_dim = hidden_dims[i] if i > 0 else input_dim
self.encoder = nn.Sequential(*encoder_layers)
self.decoder = nn.Sequential(*decoder_layers)
def forward(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
Predictive Cost Modeling
Time Series Forecasting with Neural Networks:
import pytorch_lightning as pl
from pytorch_forecasting import TimeSeriesDataSet, NBeats
import pandas as pd
class CostForecastingModel:
def __init__(self):
self.model = None
self.training_data = None
def prepare_data(self, cost_history: pd.DataFrame):
# Convert cost history to time series format
self.training_data = TimeSeriesDataSet(
cost_history,
time_idx="day",
target="cost",
group_ids=["client_id", "service"],
min_encoder_length=30,
max_encoder_length=90,
min_prediction_length=7,
max_prediction_length=30,
static_categoricals=["client_id", "service"],
time_varying_known_reals=["day_of_week", "month", "quarter"],
time_varying_unknown_reals=["cost"],
)
def train_model(self):
self.model = NBeats.from_dataset(
self.training_data,
learning_rate=3e-2,
weight_decay=1e-8,
widths=[32, 512],
backcast_loss_ratio=1.0,
)
trainer = pl.Trainer(max_epochs=50, gpus=1)
trainer.fit(self.model, self.training_data)
Reinforcement Learning for Cost Optimization
Deep Q-Network for Resource Allocation:
import gym
import torch
import torch.nn as nn
import numpy as np
from collections import deque
import random
class CloudCostEnvironment(gym.Env):
def __init__(self, client_config: Dict):
super().__init__()
self.client_config = client_config
self.action_space = gym.spaces.Discrete(5) # Scale up, down, maintain, stop, start
self.observation_space = gym.spaces.Box(
low=0, high=np.inf, shape=(10,), dtype=np.float32
)
self.current_cost = 0
self.performance_score = 1.0
def step(self, action):
# Simulate cost and performance changes based on action
cost_change, performance_change = self._simulate_action(action)
self.current_cost += cost_change
self.performance_score += performance_change
# Calculate reward (negative cost + performance bonus)
reward = -cost_change + (performance_change * 10)
# Check if episode is done
done = self.current_cost > self.client_config['max_budget']
obs = self._get_observation()
return obs, reward, done, {}
def _simulate_action(self, action):
# Implementation of cost and performance simulation
pass
class DQNAgent:
def __init__(self, state_size, action_size):
self.state_size = state_size
self.action_size = action_size
self.memory = deque(maxlen=2000)
self.epsilon = 1.0
self.epsilon_min = 0.01
self.epsilon_decay = 0.995
self.learning_rate = 0.001
self.q_network = self._build_model()
self.target_network = self._build_model()
def _build_model(self):
model = nn.Sequential(
nn.Linear(self.state_size, 64),
nn.ReLU(),
nn.Linear(64, 64),
nn.ReLU(),
nn.Linear(64, self.action_size)
)
return model
Multi-Tenant Architecture for Service Organizations
Client Isolation and Security
Tenant Management System:
from sqlalchemy import create_engine, Column, String, Integer, JSON, DateTime
from sqlalchemy.ext.declarative import declarative_base
from sqlalchemy.orm import sessionmaker
import hashlib
import secrets
Base = declarative_base()
class Tenant(Base):
__tablename__ = 'tenants'
id = Column(String, primary_key=True)
name = Column(String, nullable=False)
api_key_hash = Column(String, nullable=False)
config = Column(JSON, default={})
created_at = Column(DateTime)
def generate_api_key(self):
api_key = secrets.token_urlsafe(32)
self.api_key_hash = hashlib.sha256(api_key.encode()).hexdigest()
return api_key
class TenantManager:
def __init__(self, database_url: str):
self.engine = create_engine(database_url)
self.SessionLocal = sessionmaker(bind=self.engine)
def create_tenant(self, name: str, config: Dict) -> Tuple[str, str]:
tenant = Tenant(
id=secrets.token_urlsafe(16),
name=name,
config=config
)
api_key = tenant.generate_api_key()
with self.SessionLocal() as session:
session.add(tenant)
session.commit()
return tenant.id, api_key
Data Isolation with Row-Level Security:
-- PostgreSQL RLS for tenant data isolation
CREATE POLICY tenant_isolation ON cost_data
FOR ALL TO application_role
USING (tenant_id = current_setting('app.current_tenant'));
-- Function to set tenant context
CREATE OR REPLACE FUNCTION set_tenant_context(tenant_id TEXT)
RETURNS VOID AS $$
BEGIN
PERFORM set_config('app.current_tenant', tenant_id, true);
END;
$$ LANGUAGE plpgsql;
Scalable Agent Deployment
Kubernetes Operator for Agent Management:
apiVersion: apiextensions.k8s.io/v1
kind: CustomResourceDefinition
metadata:
name: costagents.ai.company.com
spec:
group: ai.company.com
versions:
- name: v1
served: true
storage: true
schema:
openAPIV3Schema:
type: object
properties:
spec:
type: object
properties:
tenantId:
type: string
agentType:
type: string
enum: ["cost-monitor", "optimizer", "forecaster"]
resources:
type: object
properties:
cpu:
type: string
memory:
type: string
modelConfig:
type: object
scope: Namespaced
names:
plural: costagents
singular: costagent
kind: CostAgent
Advanced AI Integration Patterns
Multi-Model Ensemble Approach
Model Router and Ensemble:
from typing import List, Dict, Any
import numpy as np
from sklearn.metrics import mean_squared_error
class ModelEnsemble:
def __init__(self):
self.models = {}
self.weights = {}
self.performance_history = {}
def add_model(self, name: str, model: Any, weight: float = 1.0):
self.models[name] = model
self.weights[name] = weight
self.performance_history[name] = deque(maxlen=100)
def predict(self, data: Any) -> Dict[str, Any]:
predictions = {}
for name, model in self.models.items():
try:
if name.startswith('ollama_'):
# Handle Ollama model inference
predictions[name] = self._query_ollama_model(model, data)
elif name.startswith('mistral_'):
# Handle Mistral model inference
predictions[name] = self._query_mistral_model(model, data)
else:
# Handle scikit-learn or other models
predictions[name] = model.predict(data)
except Exception as e:
print(f"Model {name} failed: {e}")
continue
# Weight predictions based on recent performance
final_prediction = self._weighted_ensemble(predictions)
return final_prediction
def _weighted_ensemble(self, predictions: Dict) -> Any:
# Implement weighted averaging based on model performance
pass
class IntelligentModelRouter:
def __init__(self):
self.routing_rules = {}
self.model_capabilities = {}
def route_request(self, request_type: str, complexity: float, latency_req: float):
# Route to appropriate model based on request characteristics
if request_type == "cost_analysis" and complexity < 0.5:
return "mistral_7b" # Fast, efficient model
elif request_type == "optimization" and latency_req > 10:
return "llama3_70b" # More capable model when time allows
else:
return "ensemble" # Use ensemble for complex decisions
Real-Time Streaming AI
Streaming Cost Analysis with Kafka Streams:
from kafka import KafkaConsumer, KafkaProducer
import json
import asyncio
from typing import AsyncGenerator
class StreamingCostAnalyzer:
def __init__(self, model_endpoint: str):
self.model_endpoint = model_endpoint
self.consumer = KafkaConsumer(
'cost-events',
bootstrap_servers=['localhost:9092'],
value_deserializer=lambda m: json.loads(m.decode('utf-8'))
)
self.producer = KafkaProducer(
bootstrap_servers=['localhost:9092'],
value_serializer=lambda x: json.dumps(x).encode('utf-8')
)
async def process_cost_stream(self):
async for message in self._async_consume():
# Real-time cost analysis
analysis_result = await self._analyze_cost_event(message.value)
# Emit results
await self._emit_analysis_result(analysis_result)
async def _analyze_cost_event(self, event: Dict) -> Dict:
# Use streaming-optimized model for real-time analysis
prompt = f"Analyze this cost event: {json.dumps(event)}"
response = await self._query_model(prompt)
return {
'event_id': event['id'],
'analysis': response,
'timestamp': time.time(),
'confidence': self._calculate_confidence(response)
}
Monitoring and Observability
Comprehensive Monitoring Stack
Agent Health Monitoring:
from prometheus_client import Counter, Histogram, Gauge, start_http_server
import time
import logging
class AgentMetrics:
def __init__(self):
self.decision_counter = Counter('agent_decisions_total', 'Total decisions made', ['agent_type', 'decision_type'])
self.response_time = Histogram('agent_response_time_seconds', 'Agent response time')
self.active_agents = Gauge('active_agents', 'Number of active agents', ['agent_type'])
self.cost_savings = Counter('cost_savings_total', 'Total cost savings achieved', ['client_id'])
def record_decision(self, agent_type: str, decision_type: str):
self.decision_counter.labels(agent_type=agent_type, decision_type=decision_type).inc()
def record_response_time(self, duration: float):
self.response_time.observe(duration)
# Distributed tracing with OpenTelemetry
from opentelemetry import trace
from opentelemetry.exporter.jaeger.thrift import JaegerExporter
from opentelemetry.sdk.trace import TracerProvider
from opentelemetry.sdk.trace.export import BatchSpanProcessor
tracer = trace.get_tracer(__name__)
class TracedCostAgent:
def __init__(self):
self.metrics = AgentMetrics()
async def make_cost_decision(self, request: Dict):
with tracer.start_as_current_span("cost_decision") as span:
span.set_attribute("client_id", request['client_id'])
span.set_attribute("request_type", request['type'])
start_time = time.time()
try:
result = await self._process_request(request)
span.set_attribute("decision", result['decision'])
return result
finally:
duration = time.time() - start_time
self.metrics.record_response_time(duration)
Automated Testing and Validation
Agent Behavior Testing:
import pytest
from unittest.mock import AsyncMock, patch
import asyncio
class TestCostOptimizationAgent:
@pytest.fixture
async def agent(self):
return CostOptimizationAgent(
model_endpoint="http://localhost:11434",
client_config={"max_cost": 1000, "min_performance": 0.8}
)
@pytest.mark.asyncio
async def test_cost_spike_detection(self, agent):
# Mock cost data with spike
cost_data = {
'current_cost': 1500,
'historical_average': 800,
'client_id': 'test_client'
}
with patch.object(agent, '_query_model') as mock_query:
mock_query.return_value = {
'anomaly_detected': True,
'recommended_action': 'scale_down',
'confidence': 0.95
}
result = await agent.analyze_cost_anomaly(cost_data)
assert result['anomaly_detected'] is True
assert result['recommended_action'] == 'scale_down'
@pytest.mark.asyncio
async def test_multi_agent_coordination(self):
# Test agent communication and coordination
pass
# Load testing for agent scalability
from locust import HttpUser, task, between
class AgentLoadTest(HttpUser):
wait_time = between(1, 3)
@task
def analyze_costs(self):
cost_data = {
'client_id': 'load_test_client',
'costs': [100, 150, 200, 180, 220],
'timestamp': time.time()
}
self.client.post("/api/v1/analyze-costs", json=cost_data)
@task
def get_recommendations(self):
self.client.get("/api/v1/recommendations/load_test_client")
Business Intelligence and Reporting
Automated Report Generation
AI-Powered Cost Reports:
from jinja2 import Template
import matplotlib.pyplot as plt
import pandas as pd
from datetime import datetime, timedelta
class IntelligentReporter:
def __init__(self, llm_client):
self.llm_client = llm_client
self.report_templates = {}
async def generate_executive_summary(self, cost_data: Dict, client_id: str) -> str:
# Use LLM to generate natural language insights
prompt = f"""
Based on the following cost data for client {client_id}, generate an executive summary:
Total Cost: ${cost_data['total_cost']:,.2f}
Month-over-Month Change: {cost_data['mom_change']:.1f}%
Top Cost Drivers: {', '.join(cost_data['top_drivers'])}
Optimization Opportunities: {cost_data['savings_potential']}
Generate a professional executive summary highlighting key insights and recommendations.
"""
response = await self.llm_client.generate(prompt)
return response
async def create_comprehensive_report(self, client_id: str, period: str) -> Dict:
# Gather data from multiple sources
cost_data = await self._fetch_cost_data(client_id, period)
savings_data = await self._fetch_savings_data(client_id, period)
forecast_data = await self._generate_forecast(client_id)
# Generate visualizations
charts = await self._create_charts(cost_data)
# Generate AI insights
executive_summary = await self.generate_executive_summary(cost_data, client_id)
recommendations = await self._generate_recommendations(cost_data, savings_data)
return {
'client_id': client_id,
'period': period,
'executive_summary': executive_summary,
'cost_breakdown': cost_data,
'savings_achieved': savings_data,
'forecast': forecast_data,
'recommendations': recommendations,
'charts': charts,
'generated_at': datetime.now().isoformat()
}
Security and Compliance Framework
AI Model Security
Model Input Validation and Sanitization:
import re
from typing import Any, Dict
import bleach
class SecureModelInterface:
def __init__(self):
self.input_validators = {
'cost_analysis': self._validate_cost_input,
'optimization': self._validate_optimization_input
}
self.max_input_length = 10000
self.allowed_tags = []
def sanitize_input(self, input_data: Any) -> Any:
if isinstance(input_data, str):
# Remove potentially harmful content
sanitized = bleach.clean(input_data, tags=self.allowed_tags, strip=True)
# Validate length
if len(sanitized) > self.max_input_length:
raise ValueError("Input too long")
# Check for injection patterns
if self._detect_injection_patterns(sanitized):
raise ValueError("Potentially malicious input detected")
return sanitized
elif isinstance(input_data, dict):
return {k: self.sanitize_input(v) for k, v in input_data.items()}
return input_data
def _detect_injection_patterns(self, text: str) -> bool:
# Check for common injection patterns
patterns = [
r'<script.*?>.*?</script>',
r'javascript:',
r'data:text/html',
r'vbscript:',
r'onload\s*=',
r'onerror\s*='
]
for pattern in patterns:
if re.search(pattern, text, re.IGNORECASE | re.DOTALL):
return True
return False
# Audit logging for all AI decisions
class AuditLogger:
def __init__(self, log_level: str = "INFO"):
self.logger = logging.getLogger("agent_audit")
self.logger.setLevel(getattr(logging, log_level))
handler = logging.StreamHandler()
formatter = logging.Formatter(
'%(asctime)s - %(name)s - %(levelname)s - %(message)s'
)
handler.setFormatter(formatter)
self.logger.addHandler(handler)
def log_decision(self, agent_id: str, client_id: str, decision: Dict, reasoning: str):
audit_entry = {
'timestamp': datetime.now().isoformat(),
'agent_id': agent_id,
'client_id': client_id,
'decision': decision,
'reasoning': reasoning,
'model_version': self._get_model_version(),
'confidence_score': decision.get('confidence', 0.0)
}
self.logger.info(f"DECISION: {json.dumps(audit_entry)}")
def log_action_taken(self, agent_id: str, client_id: str, action: Dict, result: Dict):
audit_entry = {
'timestamp': datetime.now().isoformat(),
'agent_id': agent_id,
'client_id': client_id,
'action': action,
'result': result,
'success': result.get('success', False)
}
self.logger.info(f"ACTION: {json.dumps(audit_entry)}")
Compliance and Governance
Policy Engine for Cost Management:
from dataclasses import dataclass
from typing import List, Callable, Any
from enum import Enum
class PolicyType(Enum):
COST_LIMIT = "cost_limit"
RESOURCE_CONSTRAINT = "resource_constraint"
APPROVAL_REQUIRED = "approval_required"
COMPLIANCE_RULE = "compliance_rule"
@dataclass
class Policy:
id: str
name: str
policy_type: PolicyType
conditions: Dict[str, Any]
actions: List[str]
priority: int
active: bool = True
class PolicyEngine:
def __init__(self):
self.policies: Dict[str, Policy] = {}
self.rule_evaluators: Dict[PolicyType, Callable] = {
PolicyType.COST_LIMIT: self._evaluate_cost_limit,
PolicyType.RESOURCE_CONSTRAINT: self._evaluate_resource_constraint,
PolicyType.APPROVAL_REQUIRED: self._evaluate_approval_requirement,
PolicyType.COMPLIANCE_RULE: self._evaluate_compliance_rule
}
def add_policy(self, policy: Policy):
self.policies[policy.id] = policy
async def evaluate_action(self, action: Dict, context: Dict) -> Dict:
"""Evaluate if an action is allowed based on active policies"""
evaluation_results = []
# Sort policies by priority
sorted_policies = sorted(
[p for p in self.policies.values() if p.active],
key=lambda x: x.priority,
reverse=True
)
for policy in sorted_policies:
evaluator = self.rule_evaluators.get(policy.policy_type)
if evaluator:
result = await evaluator(policy, action, context)
evaluation_results.append({
'policy_id': policy.id,
'policy_name': policy.name,
'allowed': result['allowed'],
'reason': result['reason'],
'required_approvals': result.get('required_approvals', [])
})
# Determine final decision
allowed = all(result['allowed'] for result in evaluation_results)
required_approvals = []
for result in evaluation_results:
required_approvals.extend(result.get('required_approvals', []))
return {
'allowed': allowed,
'policy_evaluations': evaluation_results,
'required_approvals': list(set(required_approvals))
}
async def _evaluate_cost_limit(self, policy: Policy, action: Dict, context: Dict) -> Dict:
current_cost = context.get('current_monthly_cost', 0)
projected_cost = current_cost + action.get('cost_impact', 0)
cost_limit = policy.conditions.get('monthly_limit', float('inf'))
if projected_cost > cost_limit:
return {
'allowed': False,
'reason': f"Action would exceed monthly cost limit of ${cost_limit:,.2f}"
}
return {'allowed': True, 'reason': 'Within cost limits'}
async def _evaluate_resource_constraint(self, policy: Policy, action: Dict, context: Dict) -> Dict:
# Implement resource constraint evaluation
return {'allowed': True, 'reason': 'Resource constraints satisfied'}
async def _evaluate_approval_requirement(self, policy: Policy, action: Dict, context: Dict) -> Dict:
cost_impact = action.get('cost_impact', 0)
approval_threshold = policy.conditions.get('cost_threshold', 1000)
if abs(cost_impact) > approval_threshold:
return {
'allowed': False,
'reason': f"Action requires approval (cost impact: ${cost_impact:,.2f})",
'required_approvals': policy.conditions.get('approvers', ['manager'])
}
return {'allowed': True, 'reason': 'No approval required'}
async def _evaluate_compliance_rule(self, policy: Policy, action: Dict, context: Dict) -> Dict:
# Implement compliance rule evaluation (PCI, HIPAA, SOX, etc.)
compliance_tags = context.get('compliance_tags', [])
required_tags = policy.conditions.get('required_tags', [])
if not all(tag in compliance_tags for tag in required_tags):
return {
'allowed': False,
'reason': f"Missing required compliance tags: {set(required_tags) - set(compliance_tags)}"
}
return {'allowed': True, 'reason': 'Compliance requirements met'}
Advanced Model Integration Techniques
Hybrid Local-Cloud Model Architecture
Intelligent Model Selection:
class HybridModelOrchestrator:
def __init__(self):
self.local_models = {
'ollama_llama3': 'http://localhost:11434/api/generate',
'ollama_mistral': 'http://localhost:11434/api/generate',
'ollama_codellama': 'http://localhost:11434/api/generate'
}
self.cloud_models = {
'claude': 'https://api.anthropic.com/v1/messages',
'mistral_large': 'https://api.mistral.ai/v1/chat/completions'
}
self.model_characteristics = {
'ollama_llama3': {'latency': 'low', 'cost': 'free', 'privacy': 'high', 'capability': 'medium'},
'ollama_mistral': {'latency': 'low', 'cost': 'free', 'privacy': 'high', 'capability': 'medium'},
'claude': {'latency': 'medium', 'cost': 'medium', 'privacy': 'medium', 'capability': 'high'},
'mistral_large': {'latency': 'medium', 'cost': 'low', 'privacy': 'medium', 'capability': 'high'}
}
async def select_optimal_model(self, task_type: str, requirements: Dict) -> str:
"""Select the best model based on task requirements"""
# Define selection criteria
if requirements.get('privacy_critical', False):
# Use only local models for sensitive data
candidates = list(self.local_models.keys())
else:
candidates = list(self.local_models.keys()) + list(self.cloud_models.keys())
# Score models based on requirements
scored_models = []
for model in candidates:
score = self._calculate_model_score(model, task_type, requirements)
scored_models.append((model, score))
# Return best scoring model
return max(scored_models, key=lambda x: x[1])[0]
def _calculate_model_score(self, model: str, task_type: str, requirements: Dict) -> float:
characteristics = self.model_characteristics[model]
score = 0.0
# Latency scoring
if requirements.get('max_latency', 10) < 2:
score += 3 if characteristics['latency'] == 'low' else 0
# Cost scoring
if requirements.get('cost_sensitive', False):
score += 2 if characteristics['cost'] == 'free' else 0
# Privacy scoring
if requirements.get('privacy_critical', False):
score += 4 if characteristics['privacy'] == 'high' else 0
# Capability scoring for complex tasks
if task_type in ['complex_analysis', 'strategic_planning']:
score += 3 if characteristics['capability'] == 'high' else 1
return score
async def execute_with_fallback(self, prompt: str, task_type: str, requirements: Dict) -> Dict:
"""Execute request with automatic fallback to alternative models"""
primary_model = await self.select_optimal_model(task_type, requirements)
try:
return await self._query_model(primary_model, prompt)
except Exception as e:
# Fallback strategy
fallback_models = [m for m in self.model_characteristics.keys() if m != primary_model]
for fallback_model in fallback_models:
try:
result = await self._query_model(fallback_model, prompt)
# Log fallback usage
self._log_fallback(primary_model, fallback_model, str(e))
return result
except Exception:
continue
raise Exception("All models failed")
async def _query_model(self, model_name: str, prompt: str) -> Dict:
if model_name in self.local_models:
return await self._query_ollama(model_name, prompt)
else:
return await self._query_cloud_model(model_name, prompt)
async def _query_ollama(self, model_name: str, prompt: str) -> Dict:
model_key = model_name.split('_')[1] # Extract model name (llama3, mistral, etc.)
payload = {
"model": model_key,
"prompt": prompt,
"stream": False,
"options": {
"temperature": 0.1,
"top_p": 0.9,
"num_predict": 512
}
}
async with httpx.AsyncClient() as client:
response = await client.post(
self.local_models[model_name],
json=payload,
timeout=30.0
)
response.raise_for_status()
return response.json()
Advanced Prompt Engineering for Cost Management
Domain-Specific Prompt Templates:
class CostManagementPrompts:
def __init__(self):
self.templates = {
'anomaly_analysis': """
You are a cloud cost optimization expert. Analyze the following cost data and identify anomalies:
Cost Data:
{cost_data}
Context:
- Historical average: ${historical_avg}
- Current cost: ${current_cost}
- Time period: {time_period}
- Services involved: {services}
Please provide:
1. Anomaly detection (Yes/No) with confidence score
2. Root cause analysis
3. Recommended immediate actions
4. Potential cost impact if not addressed
Format your response as JSON with the following structure:
{{
"anomaly_detected": boolean,
"confidence_score": float,
"root_cause": "string",
"immediate_actions": ["action1", "action2"],
"cost_impact": float,
"reasoning": "detailed explanation"
}}
""",
'optimization_recommendation': """
You are an expert cloud architect focused on cost optimization. Given the following resource utilization data, provide optimization recommendations:
Resource Data:
{resource_data}
Current Configuration:
{current_config}
Performance Requirements:
{performance_requirements}
Budget Constraints:
{budget_constraints}
Provide specific, actionable recommendations that:
1. Reduce costs while maintaining or improving performance
2. Consider business requirements and constraints
3. Include estimated cost savings
4. Prioritize recommendations by impact and effort
Format as JSON:
{{
"recommendations": [
{{
"action": "string",
"estimated_savings": float,
"effort_level": "low|medium|high",
"risk_level": "low|medium|high",
"implementation_steps": ["step1", "step2"],
"expected_timeline": "string"
}}
],
"total_potential_savings": float,
"implementation_priority": ["rec1", "rec2", "rec3"]
}}
""",
'executive_summary': """
Create an executive summary for cloud cost management based on the following data:
Financial Summary:
- Total monthly cost: ${total_cost}
- Month-over-month change: {mom_change}%
- Year-over-year change: {yoy_change}%
- Budget utilization: {budget_utilization}%
Key Metrics:
{key_metrics}
Optimization Actions Taken:
{actions_taken}
Upcoming Initiatives:
{upcoming_initiatives}
Write a professional executive summary that:
1. Highlights key financial performance
2. Explains significant changes
3. Summarizes optimization impact
4. Outlines strategic recommendations
5. Uses business-friendly language (avoid technical jargon)
Keep it concise (200-300 words) and focus on business value.
"""
}
def get_prompt(self, template_name: str, **kwargs) -> str:
if template_name not in self.templates:
raise ValueError(f"Template {template_name} not found")
return self.templates[template_name].format(**kwargs)
def create_chain_of_thought_prompt(self, base_prompt: str, thinking_steps: List[str]) -> str:
"""Create a chain-of-thought prompt for complex reasoning"""
cot_prefix = """
Before providing your final answer, think through this step by step:
"""
for i, step in enumerate(thinking_steps, 1):
cot_prefix += f"{i}. {step}\n"
cot_prefix += "\nNow, work through each step and provide your final answer:\n\n"
return cot_prefix + base_prompt
Multi-Modal AI Integration
Integration with Vision Models for Infrastructure Diagrams:
class MultiModalCostAnalyzer:
def __init__(self):
self.vision_models = {
'diagram_analysis': 'llava:latest', # Ollama vision model
'chart_interpretation': 'bakllava:latest'
}
async def analyze_architecture_diagram(self, image_path: str, cost_context: Dict) -> Dict:
"""Analyze infrastructure diagrams to identify cost optimization opportunities"""
# Read image
with open(image_path, 'rb') as img_file:
image_data = base64.b64encode(img_file.read()).decode()
prompt = f"""
Analyze this cloud architecture diagram and identify potential cost optimization opportunities.
Consider the following cost context:
- Current monthly spend: ${cost_context['monthly_spend']}
- Top cost drivers: {', '.join(cost_context['top_drivers'])}
- Performance requirements: {cost_context['performance_requirements']}
Look for:
1. Over-provisioned resources
2. Unnecessary redundancy
3. Inefficient data flow patterns
4. Missing cost optimization services
5. Opportunities for serverless migration
Provide specific, actionable recommendations with estimated cost impact.
"""
# Query vision model through Ollama
response = await self._query_vision_model('llava:latest', prompt, image_data)
return {
'diagram_analysis': response,
'cost_optimization_score': self._calculate_optimization_score(response),
'recommended_actions': self._extract_actions(response)
}
async def interpret_cost_charts(self, chart_images: List[str]) -> Dict:
"""Interpret cost trend charts and graphs"""
interpretations = []
for chart_path in chart_images:
with open(chart_path, 'rb') as img_file:
image_data = base64.b64encode(img_file.read()).decode()
prompt = """
Analyze this cost chart/graph and provide insights:
1. Identify trends and patterns
2. Spot anomalies or unusual spikes
3. Determine seasonality effects
4. Suggest areas for investigation
5. Provide forecasting insights
Be specific about time periods, cost values, and percentage changes you observe.
"""
interpretation = await self._query_vision_model('bakllava:latest', prompt, image_data)
interpretations.append(interpretation)
return {
'chart_interpretations': interpretations,
'combined_insights': await self._synthesize_chart_insights(interpretations)
}
async def _query_vision_model(self, model: str, prompt: str, image_data: str) -> str:
payload = {
"model": model,
"prompt": prompt,
"images": [image_data],
"stream": False
}
async with httpx.AsyncClient() as client:
response = await client.post(
"http://localhost:11434/api/generate",
json=payload,
timeout=60.0
)
response.raise_for_status()
return response.json()['response']
Performance Optimization and Scaling
Distributed Agent Architecture
Agent Cluster Management:
import asyncio
import aioredis
from typing import List, Dict, Any
from dataclasses import dataclass, asdict
from datetime import datetime, timedelta
@dataclass
class AgentNode:
node_id: str
agent_type: str
status: str
last_heartbeat: datetime
current_load: float
max_capacity: int
client_assignments: List[str]
class DistributedAgentManager:
def __init__(self, redis_url: str):
self.redis_url = redis_url
self.redis = None
self.local_agents: Dict[str, Any] = {}
self.node_id = secrets.token_urlsafe(8)
async def initialize(self):
self.redis = await aioredis.from_url(self.redis_url)
await self.register_node()
# Start background tasks
asyncio.create_task(self.heartbeat_loop())
asyncio.create_task(self.load_balancer_loop())
async def register_node(self):
"""Register this node in the distributed cluster"""
node_info = AgentNode(
node_id=self.node_id,
agent_type="multi_purpose",
status="active",
last_heartbeat=datetime.now(),
current_load=0.0,
max_capacity=100,
client_assignments=[]
)
await self.redis.hset(
"agent_nodes",
self.node_id,
json.dumps(asdict(node_info), default=str)
)
async def heartbeat_loop(self):
"""Send periodic heartbeats to maintain cluster membership"""
while True:
try:
await self.redis.hset(
"agent_nodes",
self.node_id,
json.dumps({
"node_id": self.node_id,
"status": "active",
"last_heartbeat": datetime.now().isoformat(),
"current_load": self.calculate_current_load(),
"client_assignments": list(self.local_agents.keys())
})
)
await asyncio.sleep(30) # Heartbeat every 30 seconds
except Exception as e:
print(f"Heartbeat error: {e}")
await asyncio.sleep(5)
async def distribute_work(self, task: Dict) -> str:
"""Distribute work to the most appropriate agent node"""
# Get all active nodes
nodes = await self.get_active_nodes()
# Select best node based on load and capabilities
best_node = self.select_optimal_node(nodes, task)
if best_node == self.node_id:
# Execute locally
return await self.execute_local_task(task)
else:
# Send to remote node
return await self.send_remote_task(best_node, task)
def select_optimal_node(self, nodes: List[Dict], task: Dict) -> str:
"""Select the optimal node for task execution"""
# Simple load-based selection (can be enhanced with ML)
available_nodes = [
node for node in nodes
if node['current_load'] < 0.8 and node['status'] == 'active'
]
if not available_nodes:
return self.node_id # Fallback to local execution
# Select node with lowest load
best_node = min(available_nodes, key=lambda x: x['current_load'])
return best_node['node_id']
async def get_active_nodes(self) -> List[Dict]:
"""Get list of all active agent nodes"""
node_data = await self.redis.hgetall("agent_nodes")
nodes = []
for node_id, data in node_data.items():
node_info = json.loads(data)
# Check if node is still alive (heartbeat within last 2 minutes)
last_heartbeat = datetime.fromisoformat(node_info['last_heartbeat'])
if datetime.now() - last_heartbeat < timedelta(minutes=2):
nodes.append(node_info)
return nodes
class AdaptiveLoadBalancer:
def __init__(self):
self.load_history = deque(maxlen=100)
self.response_times = deque(maxlen=100)
self.error_rates = deque(maxlen=100)
def calculate_node_score(self, node: Dict, task_type: str) -> float:
"""Calculate a score for node selection based on multiple factors"""
# Base score from current load (lower is better)
load_score = 1.0 - node['current_load']
# Historical performance score
performance_score = self.get_historical_performance(node['node_id'])
# Task affinity score (some nodes might be better for certain tasks)
affinity_score = self.get_task_affinity(node['node_id'], task_type)
# Weighted combination
total_score = (load_score * 0.4 + performance_score * 0.4 + affinity_score * 0.2)
return total_score
def get_historical_performance(self, node_id: str) -> float:
# Implementation would track historical performance metrics
return 0.8 # Placeholder
def get_task_affinity(self, node_id: str, task_type: str) -> float:
# Some nodes might be optimized for specific task types
return 0.5 # Placeholder
Caching and Optimization Strategies
Intelligent Caching for AI Responses:
import hashlib
from typing import Optional, Tuple
import pickle
import asyncio
class IntelligentCache:
def __init__(self, redis_client, ttl_seconds: int = 3600):
self.redis = redis_client
self.ttl = ttl_seconds
self.hit_rate_window = deque(maxlen=1000)
async def get_or_compute(self,
key_data: Dict,
compute_func: Callable,
cache_strategy: str = 'standard') -> Tuple[Any, bool]:
"""Get cached result or compute new one with intelligent caching strategies"""
cache_key = self._generate_cache_key(key_data)
# Try to get from cache
cached_result = await self._get_cached_result(cache_key)
if cached_result is not None:
self.hit_rate_window.append(1) # Cache hit
return cached_result, True
# Cache miss - compute result
self.hit_rate_window.append(0) # Cache miss
result = await compute_func()
# Apply caching strategy
if cache_strategy == 'standard':
await self._cache_result(cache_key, result, self.ttl)
elif cache_strategy == 'adaptive':
ttl = await self._calculate_adaptive_ttl(key_data, result)
await self._cache_result(cache_key, result, ttl)
elif cache_strategy == 'predictive':
await self._predictive_cache(key_data, result)
return result, False
def _generate_cache_key(self, key_data: Dict) -> str:
"""Generate deterministic cache key from input data"""
# Sort keys to ensure consistent ordering
sorted_data = json.dumps(key_data, sort_keys=True)
# Create hash
return hashlib.sha256(sorted_data.encode()).hexdigest()
async def _get_cached_result(self, cache_key: str) -> Optional[Any]:
"""Retrieve result from cache"""
try:
cached_data = await self.redis.get(f"cache:{cache_key}")
if cached_data:
return pickle.loads(cached_data)
except Exception as e:
print(f"Cache retrieval error: {e}")
return None
async def _cache_result(self, cache_key: str, result: Any, ttl: int):
"""Store result in cache"""
try:
serialized_result = pickle.dumps(result)
await self.redis.setex(f"cache:{cache_key}", ttl, serialized_result)
except Exception as e:
print(f"Cache storage error: {e}")
async def _calculate_adaptive_ttl(self, key_data: Dict, result: Any) -> int:
"""Calculate adaptive TTL based on data characteristics"""
base_ttl = self.ttl
# Adjust TTL based on result confidence
if isinstance(result, dict) and 'confidence' in result:
confidence = result['confidence']
# Higher confidence = longer TTL
ttl_multiplier = 0.5 + (confidence * 1.5)
base_ttl = int(base_ttl * ttl_multiplier)
# Adjust based on data volatility
if 'real_time' in key_data and key_data['real_time']:
base_ttl = min(base_ttl, 300) # Max 5 minutes for real-time data
# Adjust based on cost of computation
computation_cost = key_data.get('computation_cost', 'medium')
if computation_cost == 'high':
base_ttl *= 2 # Cache longer for expensive computations
elif computation_cost == 'low':
base_ttl = int(base_ttl * 0.5) # Shorter cache for cheap computations
return max(60, min(base_ttl, 86400)) # Between 1 minute and 1 day
async def _predictive_cache(self, key_data: Dict, result: Any):
"""Implement predictive caching for likely future requests"""
# Analyze patterns to predict future cache needs
similar_keys = await self._find_similar_cache_patterns(key_data)
for similar_key in similar_keys:
# Pre-warm cache for similar requests
asyncio.create_task(self._precompute_similar_request(similar_key))
def get_cache_stats(self) -> Dict:
"""Get cache performance statistics"""
if not self.hit_rate_window:
return {'hit_rate': 0.0, 'total_requests': 0}
hit_rate = sum(self.hit_rate_window) / len(self.hit_rate_window)
return {
'hit_rate': hit_rate,
'total_requests': len(self.hit_rate_window),
'cache_hits': sum(self.hit_rate_window),
'cache_misses': len(self.hit_rate_window) - sum(self.hit_rate_window)
}
Conclusion and Future Directions
Building agentic AI systems for cloud cost management represents a significant evolution in how organizations approach cost optimization. By leveraging open-source models through platforms like Ollama, combined with cloud-based AI services from Anthropic and Mistral, organizations can create sophisticated, autonomous systems that continuously optimize cloud spending while maintaining performance and compliance requirements.
The key to success lies in creating a robust, scalable architecture that can adapt to changing requirements and learn from experience. The multi-agent approach allows for specialization and coordination, while the use of both local and cloud-based models provides flexibility in balancing cost, privacy, and capability requirements.
Future Enhancements
Advanced AI Capabilities:
- Integration of multimodal AI for processing infrastructure diagrams, dashboards, and documentation
- Implementation of federated learning for cross-client insights while maintaining privacy
- Development of domain-specific fine-tuned models for cloud cost optimization
Enhanced Automation:
- Autonomous contract negotiation with cloud providers
- Predictive scaling based on business events and seasonal patterns
- Integration with business intelligence systems for holistic cost optimization
Improved Decision Making:
- Causal inference models to understand the true impact of optimization actions
- Game-theoretic approaches for multi-cloud optimization
- Integration of sustainability metrics alongside cost optimization
The future of cloud cost management lies in intelligent, autonomous systems that can understand business context, predict future needs, and take proactive actions to optimize costs while ensuring performance and compliance. By implementing the architecture and techniques outlined in this guide, organizations can build powerful agentic AI systems that transform cloud cost management from a reactive discipline to a proactive, strategic advantage.
As the field continues to evolve, staying current with advances in AI models, cloud technologies, and optimization techniques will be crucial for maintaining competitive advantage in the rapidly changing landscape of cloud computing and artificial intelligence.
Sentiment Analysis with RNN End to End Project: A Technical Exploration
In today’s digital landscape, understanding sentiment from text data has become a crucial component for businesses and researchers alike. This blog post explores an end-to-end implementation of a sentiment analysis system using Recurrent Neural Networks (RNNs), with a detailed examination of the underlying code, architecture decisions, and deployment strategy.
Try the Sentiment WebApp: model Accuracy > 90%
IMDB Sentiment Analysis Webapp
Analyze the sentiment of any IMDB review using our Sentiment Analysis Tool
Launch ApplicationIntroduction to the Project
The Sentiment Analysis RNN project by Tejas K provides a comprehensive implementation of sentiment analysis that takes raw text as input and classifies it into positive, negative, or neutral categories. What makes this project stand out is its careful attention to the entire machine learning pipeline from data preprocessing to deployment.
Let’s delve into the technical aspects of this implementation.
Data Preprocessing: The Foundation
The quality of any NLP model heavily depends on how well the text data is preprocessed. The project implements several crucial preprocessing steps:
def preprocess_text(text):
# Convert to lowercase
text = text.lower()
# Remove HTML tags
text = re.sub(r'<.*?>', '', text)
# Remove special characters and numbers
text = re.sub(r'[^a-zA-Z\s]', '', text)
# Tokenize
tokens = word_tokenize(text)
# Remove stopwords
stop_words = set(stopwords.words('english'))
tokens = [word for word in tokens if word not in stop_words]
# Lemmatization
lemmatizer = WordNetLemmatizer()
tokens = [lemmatizer.lemmatize(word) for word in tokens]
return ' '.join(tokens)
This preprocessing function performs several important operations:
- Converting text to lowercase to ensure consistent processing
- Removing HTML tags that might be present in web-scraped data
- Filtering out special characters and numbers to focus on alphabetic content
- Tokenizing the text into individual words
- Removing stopwords (common words like “the”, “and”, etc.) that typically don’t carry sentiment
- Lemmatizing words to reduce them to their base form
Building the Vocabulary: Tokenization and Embedding
Before feeding text to an RNN, we need to convert words into numerical vectors. The project implements a vocabulary builder and embedding mechanism:
class Vocabulary:
def __init__(self, max_size=None):
self.word2idx = {"<PAD>": 0, "<UNK>": 1}
self.idx2word = {0: "<PAD>", 1: "<UNK>"}
self.word_count = {}
self.max_size = max_size
def add_word(self, word):
if word not in self.word_count:
self.word_count[word] = 1
else:
self.word_count[word] += 1
def build_vocab(self):
# Sort words by frequency
sorted_words = sorted(self.word_count.items(), key=lambda x: x[1], reverse=True)
# Take only max_size most common words if specified
if self.max_size:
sorted_words = sorted_words[:self.max_size-2] # -2 for <PAD> and <UNK>
# Add words to dictionaries
for word, _ in sorted_words:
idx = len(self.word2idx)
self.word2idx[word] = idx
self.idx2word[idx] = word
def text_to_indices(self, text, max_length=None):
words = text.split()
indices = [self.word2idx.get(word, self.word2idx["<UNK>"]) for word in words]
if max_length:
if len(indices) > max_length:
indices = indices[:max_length]
else:
indices += [self.word2idx["<PAD>"]] * (max_length - len(indices))
return indices
This vocabulary class:
- Maintains mappings between words and their numerical indices
- Counts word frequencies to build a vocabulary of the most common words
- Handles unknown words with a special
<UNK>token - Pads sequences to a consistent length with a
<PAD>token - Converts text to sequences of indices for model processing
The Core: RNN Model Architecture
The heart of the project is the RNN model architecture. The implementation uses PyTorch to build a flexible model that can be configured with different RNN cell types (LSTM or GRU) and embedding dimensions:
class SentimentRNN(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_dim, output_dim, n_layers,
bidirectional, dropout, pad_idx, cell_type='lstm'):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx=pad_idx)
if cell_type.lower() == 'lstm':
self.rnn = nn.LSTM(embedding_dim,
hidden_dim,
num_layers=n_layers,
bidirectional=bidirectional,
dropout=dropout if n_layers > 1 else 0,
batch_first=True)
elif cell_type.lower() == 'gru':
self.rnn = nn.GRU(embedding_dim,
hidden_dim,
num_layers=n_layers,
bidirectional=bidirectional,
dropout=dropout if n_layers > 1 else 0,
batch_first=True)
else:
raise ValueError("cell_type must be 'lstm' or 'gru'")
self.fc = nn.Linear(hidden_dim * 2 if bidirectional else hidden_dim, output_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, text, text_lengths):
# text = [batch size, seq length]
embedded = self.dropout(self.embedding(text))
# embedded = [batch size, seq length, embedding dim]
# Pack sequence for RNN efficiency
packed_embedded = nn.utils.rnn.pack_padded_sequence(embedded, text_lengths.cpu(),
batch_first=True, enforce_sorted=False)
if isinstance(self.rnn, nn.LSTM):
packed_output, (hidden, _) = self.rnn(packed_embedded)
else: # GRU
packed_output, hidden = self.rnn(packed_embedded)
# hidden = [n layers * n directions, batch size, hidden dim]
# If bidirectional, concatenate the final forward and backward hidden states
if self.rnn.bidirectional:
hidden = self.dropout(torch.cat((hidden[-2,:,:], hidden[-1,:,:]), dim=1))
else:
hidden = self.dropout(hidden[-1,:,:])
# hidden = [batch size, hidden dim * n directions]
return self.fc(hidden)
This model includes several key components:
- An embedding layer that converts word indices to dense vectors
- A configurable RNN layer (either LSTM or GRU) that processes the sequence
- Support for bidirectional processing to capture context from both directions
- Dropout for regularization to prevent overfitting
- A final fully connected layer for classification
- Efficient sequence packing to handle variable-length inputs
Training the Model: The Learning Process
The training loop implements several best practices for deep learning:
def train_model(model, train_iterator, optimizer, criterion):
model.train()
epoch_loss = 0
epoch_acc = 0
for batch in train_iterator:
optimizer.zero_grad()
text, text_lengths = batch.text
predictions = model(text, text_lengths)
loss = criterion(predictions, batch.label)
acc = calculate_accuracy(predictions, batch.label)
loss.backward()
nn.utils.clip_grad_norm_(model.parameters(), max_norm=5)
optimizer.step()
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(train_iterator), epoch_acc / len(train_iterator)
Notable aspects include:
- Setting the model to training mode with
model.train() - Zeroing gradients before each batch to prevent accumulation
- Computing loss and accuracy for monitoring training progress
- Implementing gradient clipping to prevent exploding gradients
- Updating model weights with the optimizer
- Tracking and returning average loss and accuracy
Evaluation and Testing: Measuring Performance
The evaluation function follows a similar structure but disables certain training-specific components:
def evaluate_model(model, iterator, criterion):
model.eval()
epoch_loss = 0
epoch_acc = 0
with torch.no_grad():
for batch in iterator:
text, text_lengths = batch.text
predictions = model(text, text_lengths)
loss = criterion(predictions, batch.label)
acc = calculate_accuracy(predictions, batch.label)
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
Key differences from the training function:
- Setting the model to evaluation mode with
model.eval() - Using
torch.no_grad()to disable gradient calculation for efficiency - Not performing backward passes or optimizer steps
Model Deployment: From PyTorch to Streamlit
The project’s deployment strategy involves exporting the trained PyTorch model to TorchScript for production use:
def export_model(model, vocab):
model.eval()
# Create a script module from the PyTorch model
example_text = torch.randint(0, len(vocab), (1, 10))
example_lengths = torch.tensor([10])
traced_model = torch.jit.trace(model, (example_text, example_lengths))
# Save the scripted model
torch.jit.save(traced_model, "sentiment_model.pt")
# Save the vocabulary
with open("vocab.json", "w") as f:
json.dump({
"word2idx": vocab.word2idx,
"idx2word": {int(k): v for k, v in vocab.idx2word.items()}
}, f)
The exported model is then integrated into a Streamlit application for easy access:
def load_model():
# Load the TorchScript model
model = torch.jit.load("sentiment_model.pt")
# Load vocabulary
with open("vocab.json", "r") as f:
vocab_data = json.load(f)
# Recreate vocabulary object
vocab = Vocabulary()
vocab.word2idx = vocab_data["word2idx"]
vocab.idx2word = {int(k): v for k, v in vocab_data["idx2word"].items()}
return model, vocab
def predict_sentiment(model, vocab, text):
# Preprocess text
processed_text = preprocess_text(text)
# Convert to indices
indices = vocab.text_to_indices(processed_text, max_length=100)
tensor = torch.LongTensor(indices).unsqueeze(0) # Add batch dimension
length = torch.tensor([len(indices)])
# Make prediction
model.eval()
with torch.no_grad():
prediction = model(tensor, length)
# Get probability using softmax
probabilities = F.softmax(prediction, dim=1)
# Get predicted class
predicted_class = torch.argmax(prediction, dim=1).item()
# Map to sentiment
sentiment_map = {0: "Negative", 1: "Neutral", 2: "Positive"}
return {
"sentiment": sentiment_map[predicted_class],
"confidence": probabilities[0][predicted_class].item(),
"probabilities": {
sentiment_map[i]: prob.item() for i, prob in enumerate(probabilities[0])
}
}
The Streamlit application code brings everything together in a user-friendly interface:
def main():
st.title("Sentiment Analysis with RNN")
model, vocab = load_model()
st.write("Enter text to analyze its sentiment:")
user_input = st.text_area("Text input", "")
if st.button("Analyze Sentiment"):
if user_input:
with st.spinner("Analyzing..."):
result = predict_sentiment(model, vocab, user_input)
st.write(f"**Sentiment:** {result['sentiment']}")
st.write(f"**Confidence:** {result['confidence']*100:.2f}%")
# Display probabilities
st.write("### Probability Distribution")
for sentiment, prob in result['probabilities'].items():
st.write(f"{sentiment}: {prob*100:.2f}%")
st.progress(prob)
else:
st.warning("Please enter some text to analyze.")
if __name__ == "__main__":
main()
The iframe parameters and styling ensure:
- The dark theme specified with
embed_options=dark_theme - Responsive design that works on different screen sizes
- Clean integration with the WordPress site’s aesthetics
- Proper sizing to accommodate the application’s interface
Performance Optimization and Model Improvements
The project implements several performance optimizations:
- Batch processing during training to improve GPU utilization:
def create_iterators(train_data, valid_data, test_data, batch_size=64):
train_iterator, valid_iterator, test_iterator = data.BucketIterator.splits(
(train_data, valid_data, test_data),
batch_size=batch_size,
sort_key=lambda x: len(x.text),
sort_within_batch=True,
device=device)
return train_iterator, valid_iterator, test_iterator
- Early stopping to prevent overfitting:
def train_with_early_stopping(model, train_iterator, valid_iterator,
optimizer, criterion, patience=5):
best_valid_loss = float('inf')
epochs_without_improvement = 0
for epoch in range(max_epochs):
train_loss, train_acc = train_model(model, train_iterator, optimizer, criterion)
valid_loss, valid_acc = evaluate_model(model, valid_iterator, criterion)
if valid_loss < best_valid_loss:
best_valid_loss = valid_loss
torch.save(model.state_dict(), 'best-model.pt')
epochs_without_improvement = 0
else:
epochs_without_improvement += 1
print(f'Epoch: {epoch+1}')
print(f'\tTrain Loss: {train_loss:.3f} | Train Acc: {train_acc*100:.2f}%')
print(f'\tVal. Loss: {valid_loss:.3f} | Val. Acc: {valid_acc*100:.2f}%')
if epochs_without_improvement >= patience:
print(f'Early stopping after {epoch+1} epochs')
break
# Load the best model
model.load_state_dict(torch.load('best-model.pt'))
return model
- Learning rate scheduling for better convergence:
optimizer = optim.Adam(model.parameters(), lr=2e-4)
scheduler = optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min',
factor=0.5, patience=2)
# In training loop
scheduler.step(valid_loss)
Conclusion: Putting It All Together
The Sentiment Analysis RNN project demonstrates how to build a complete NLP system from data preprocessing to web deployment. Key technical takeaways include:
- Effective text preprocessing is crucial for good model performance
- RNNs (particularly LSTMs and GRUs) excel at capturing sequential dependencies in text
- Proper training techniques like early stopping and learning rate scheduling improve model quality
- Model export and deployment bridges the gap between development and production
- Web integration makes the model accessible to end-users without technical knowledge
By embedding the Streamlit application in a WordPress site, this technical solution becomes accessible to a wider audience, showcasing how advanced NLP techniques can be applied to practical problems.
The combination of robust model architecture, efficient training procedures, and user-friendly deployment makes this project an excellent case study in applied deep learning for natural language processing.
You can explore the full implementation on GitHub or try the live demo at Streamlit App.
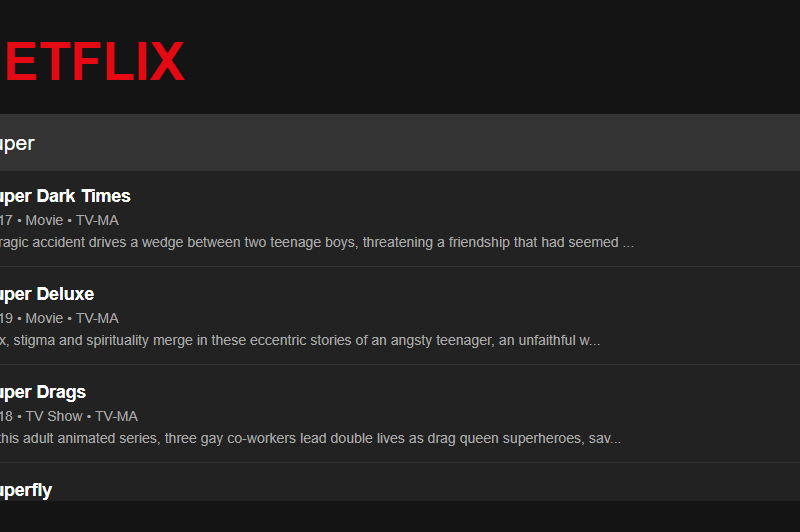
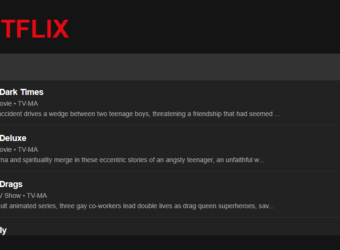
Netflix Autosuggest Search Engine
By Tejas Kamble – AI/ML Developer & Researcher | tejaskamble.com
Introduction
Have you ever used the Netflix search bar and instantly seen suggestions that seem to know exactly what you’re looking for—even before you finish typing? Inspired by this, I created a Netflix Search Engine using NLP Text Suggestions — a project that bridges the power of natural language processing (NLP) with real-time search functionalities.
In this post, I’ll walk you through the codebase hosted on my GitHub: Netflix_Search_Engine_NLP_Text_suggestion, breaking down each important part, from data loading and text preprocessing to building the suggestion logic and deploying it using Flask.
📂 Project Structure
Netflix_Search_Engine_NLP_Text_suggestion/
├── app.py ← Flask Web App
├── netflix_titles.csv ← Dataset of Netflix shows/movies
├── templates/
│ ├── index.html ← Frontend UI
├── static/
│ └── style.css ← Custom styling
├── requirements.txt ← Python dependencies
└── README.md ← Project overview
Dataset Overview
I used a dataset of Netflix titles (from Kaggle). It includes:
- Title: Name of the show/movie
- Description: Synopsis of the content
- Cast: Actors involved
- Genres, Date Added, Duration and more…
This dataset is essential for understanding user intent when making text suggestions.
Step-by-Step Breakdown of the Code
Loading the Dataset
df = pd.read_csv("netflix_titles.csv")
df.dropna(subset=['title'], inplace=True)
We load the dataset and ensure there are no missing values in the title column since that’s our search anchor.
Text Vectorization using TF-IDF
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(stop_words='english')
tfidf_matrix = vectorizer.fit_transform(df['title'])
- TF-IDF (Term Frequency-Inverse Document Frequency) is used to convert titles into numerical vectors.
- This helps quantify the importance of each word in the context of the entire dataset.
Cosine Similarity Search
from sklearn.metrics.pairwise import cosine_similarity
def get_recommendations(input_text):
input_vec = vectorizer.transform([input_text])
similarity = cosine_similarity(input_vec, tfidf_matrix)
indices = similarity.argsort()[0][-5:][::-1]
return df['title'].iloc[indices]
Here’s where the magic happens:
- The user input is vectorized.
- We compute cosine similarity with all titles.
- The top 5 most similar titles are returned as recommendations.
Flask Web Application
The search engine is hosted using a lightweight Flask backend.
@app.route("/", methods=["GET", "POST"])
def index():
if request.method == "POST":
user_input = request.form["title"]
suggestions = get_recommendations(user_input)
return render_template("index.html", suggestions=suggestions, query=user_input)
return render_template("index.html")
- Accepts user input from the HTML form
- Processes it through
get_recommendations() - Displays top matching titles
Frontend – index.html
A simple yet effective UI allows users to interact with the engine.
<form method="POST">
<input type="text" name="title" placeholder="Search for Netflix titles...">
<button type="submit">Search</button>
</form>
If suggestions are found, they’re shown dynamically below the form.
🌐 Deployment
To run this app locally:
git clone https://github.com/tejask0512/Netflix_Search_Engine_NLP_Text_suggestion
cd Netflix_Search_Engine_NLP_Text_suggestion
pip install -r requirements.txt
python app.py
Then open http://127.0.0.1:5000 in your browser!
Key Takeaways
- TF-IDF is powerful for information retrieval tasks.
- Even a simple cosine similarity search can replicate sophisticated autocomplete behavior.
- Flask makes it easy to bring machine learning to the web.
What’s Next?
Here are a few ways I plan to extend this project:
- Use BERT or Sentence Transformers for semantic similarity.
- Add spell correction and synonym support.
- Deploy it on Render, Heroku, or HuggingFace Spaces.
- Add a recommendation engine using genres, cast similarity, or collaborative filtering.
🧑💻 About Me
I’m Tejas Kamble, an AI/ML Developer & Researcher passionate about building intelligent, ethical, and multilingual human-computer interaction systems. I focus on:
- AI-driven trading strategies
- NLP-based behavioral analysis
- Real-time blockchain sentiment analysis
- Deep learning for crop disease detection
Check out more of my work on my GitHub @tejask0512
🌐 Website: tejaskamble.com
💬 Feedback & Collaboration
I’d love to hear your thoughts or collaborate on cool projects!
Let’s connect: tejaskamble.com/contact
Computer Vision for Gesture Control: Building a Hand-Controlled Mouse
Introduction
In today’s digital era, the way we interact with computers continues to evolve. Beyond the traditional keyboard and mouse, gesture recognition represents one of the most intuitive forms of human-computer interaction. By leveraging computer vision techniques and machine learning, we can create systems that interpret hand movements and translate them into computer commands.
This blog explores the development of a gesture-controlled mouse system that allows users to control their cursor and perform clicks using only hand movements captured by a webcam. We’ll dive deep into the underlying computer vision technologies, implementation details, and practical considerations for building such a system.
The Science Behind Gesture Recognition
Computer Vision Fundamentals
Computer vision is the field that enables computers to derive meaningful information from digital images or videos. At its core, it involves:
- Image Acquisition: Capturing visual data through cameras or sensors
- Image Processing: Manipulating images to enhance features or reduce noise
- Feature Detection: Identifying points of interest within an image
- Pattern Recognition: Classifying patterns or objects within the visual data
For gesture control systems, we need reliable methods to detect hands, identify their landmarks (key points), and interpret their movements.
Hand Detection and Tracking
Modern hand tracking systems typically follow a two-stage approach:
- Hand Detection: Locating the hand within the frame
- Landmark Detection: Identifying specific points on the hand (fingertips, joints, palm center)
Historically, approaches included:
- Color-based segmentation: Isolating hand regions based on skin color
- Background subtraction: Identifying moving objects against a static background
- Feature-based methods: Using handcrafted features like Haar cascades or HOG
Today’s state-of-the-art systems leverage deep learning, specifically convolutional neural networks (CNNs), for both detection and landmark identification.
MediaPipe Hands
Google’s MediaPipe Hands is currently one of the most accessible and accurate hand tracking solutions available. It provides:
- Real-time hand detection
- 21 3D landmarks per hand
- Support for multiple hands
- Cross-platform compatibility
MediaPipe uses a pipeline approach:
- A palm detector that locates hand regions
- A hand landmark model that identifies 21 key points
- A gesture recognition system built on these landmarks
Each landmark corresponds to a specific anatomical feature of the hand:
- Wrist point
- Thumb (4 points)
- Index finger (4 points)
- Middle finger (4 points)
- Ring finger (4 points)
- Pinky finger (4 points)

Sample Code
import cvzone
import cv2
cap = cv2.VideoCapture(0)
cap.set(3, 1280)
cap.set(4, 720)
detector = cvzone.HandDetector(detectionCon=0.5, maxHands=1)
while True:
# Get image frame
success, img = cap.read()
# Find the hand and its landmarks
img = detector.findHands(img)
lmList, bbox = detector.findPosition(img)
# Display
cv2.imshow("Image", img)
cv2.waitKey(1)
Building a Gesture-Controlled Mouse
System Architecture
Our gesture mouse system consists of several interconnected components:
- Input Processing: Captures and processes webcam input
- Hand Detection: Identifies hands in the frame
- Landmark Extraction: Locates the 21 key points on each hand
- Gesture Recognition: Interprets specific hand configurations as commands
- Command Execution: Translates gestures into mouse actions
Required Technologies and Libraries
To implement this system, we’ll use:
- OpenCV: For webcam capture and image processing
- MediaPipe: For hand detection and landmark tracking
- PyAutoGUI: For programmatically controlling the mouse
- NumPy: For efficient numerical operations
Implementation Details
Let’s explore the core functionality of our gesture-controlled mouse system:
1. Setting Up the Environment
First, we initialize the necessary libraries and configure MediaPipe for hand tracking:
import cv2
import mediapipe as mp
import pyautogui
import numpy as np
import time
# Initialize MediaPipe Hand solution
mp_hands = mp.solutions.hands
hands = mp_hands.Hands(
static_image_mode=False,
max_num_hands=1,
min_detection_confidence=0.7,
min_tracking_confidence=0.5
)
mp_drawing = mp.solutions.drawing_utils
# Get screen dimensions for mapping hand position to screen coordinates
screen_width, screen_height = pyautogui.size()
The MediaPipe configuration includes several important parameters:
static_image_mode=False: Optimizes for video sequence trackingmax_num_hands=1: Limits detection to one hand for simplicitymin_detection_confidence=0.7: Sets the threshold for hand detectionmin_tracking_confidence=0.5: Sets the threshold for tracking continuation
2. Capturing and Processing Video
Next, we set up the webcam capture and create the main processing loop:
# Get webcam
cap = cv2.VideoCapture(0)
while cap.isOpened():
success, image = cap.read()
if not success:
print("Failed to capture image from webcam.")
continue
# Flip the image horizontally for a more intuitive mirror view
image = cv2.flip(image, 1)
# Convert BGR image to RGB for MediaPipe
rgb_image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
# Process the image and detect hands
results = hands.process(rgb_image)
The horizontal flip creates a mirror-like experience, making the interaction more intuitive for users.
3. Hand Landmark Detection
Once we have processed the image, we extract and visualize the hand landmarks:
# Draw hand landmarks if detected
if results.multi_hand_landmarks:
for hand_landmarks in results.multi_hand_landmarks:
mp_drawing.draw_landmarks(
image, hand_landmarks, mp_hands.HAND_CONNECTIONS)
# Get the landmarks as a list
landmarks = hand_landmarks.landmark
# Process landmarks for mouse control...
Each detected hand provides 21 landmarks with normalized coordinates:
- x, y: Normalized to [0.0, 1.0] within the image
- z: Represents depth with the wrist as origin (negative values are toward the camera)
4. Implementing Mouse Movement
To control mouse movement, we map hand position to screen coordinates:
# Smoothing factors
smoothing = 5
prev_x, prev_y = 0, 0
# Inside the main loop:
# Using wrist position for mouse control
wrist = landmarks[mp_hands.HandLandmark.WRIST]
x = int(wrist.x * screen_width)
y = int(wrist.y * screen_height)
# Apply smoothing for more stable cursor movement
prev_x = prev_x + (x - prev_x) / smoothing
prev_y = prev_y + (y - prev_y) / smoothing
# Move the mouse
pyautogui.moveTo(prev_x, prev_y)
The smoothing factor reduces jitter by creating a weighted average between the current and previous positions, resulting in more fluid cursor movement.
5. Gesture Recognition for Mouse Clicks
For click actions, we detect finger tap gestures:
def detect_finger_tap(landmarks, finger_tip_idx, finger_pip_idx):
"""Detect if a finger is tapped (tip close to palm)"""
tip = landmarks[finger_tip_idx]
pip = landmarks[finger_pip_idx]
# Calculate vertical distance between tip and pip
distance = abs(tip.y - pip.y)
# If tip is below pip and close enough, it's a tap
return tip.y > pip.y and distance < tap_threshold
# In the main loop:
# Detect index finger tap for left click
if detect_finger_tap(landmarks, mp_hands.HandLandmark.INDEX_FINGER_TIP, mp_hands.HandLandmark.INDEX_FINGER_PIP):
current_time = time.time()
if current_time - last_index_tap_time > tap_cooldown:
print("Left click")
pyautogui.click()
last_index_tap_time = current_time
# Detect middle finger tap for right click
if detect_finger_tap(landmarks, mp_hands.HandLandmark.MIDDLE_FINGER_TIP, mp_hands.HandLandmark.MIDDLE_FINGER_PIP):
current_time = time.time()
if current_time - last_middle_tap_time > tap_cooldown:
print("Right click")
pyautogui.rightClick()
last_middle_tap_time = current_time
The tap detection works by:
- Measuring the vertical distance between a fingertip and its corresponding PIP joint
- Identifying a tap when the fingertip moves below the joint and within a certain distance threshold
- Implementing a cooldown period to prevent accidental multiple clicks
Implementing Scrolling Functionality
Scrolling is an essential feature for navigating documents and webpages. Let’s implement smooth scrolling control using hand gestures.
1. Pinch-to-Scroll Implementation
One of the most intuitive ways to implement scrolling is through a pinch gesture between the thumb and ring finger, followed by vertical movement:
# Global variables for tracking scroll state
scroll_active = False
scroll_start_y = 0
last_scroll_time = 0
scroll_cooldown = 0.05 # Seconds between scroll actions
scroll_sensitivity = 1.0 # Adjustable scroll sensitivity
def detect_scroll_gesture(landmarks):
"""Detect thumb and ring finger pinch for scrolling"""
thumb_tip = landmarks[mp_hands.HandLandmark.THUMB_TIP]
ring_tip = landmarks[mp_hands.HandLandmark.RING_FINGER_TIP]
# Calculate distance between thumb and ring finger
distance = np.sqrt((thumb_tip.x - ring_tip.x)**2 + (thumb_tip.y - ring_tip.y)**2)
# If thumb and ring finger are close enough, it's a pinch
return distance < 0.07 # Threshold value may need adjustment
# In the main loop:
if results.multi_hand_landmarks:
landmarks = results.multi_hand_landmarks[0].landmark
# Check for scroll gesture
is_scroll_gesture = detect_scroll_gesture(landmarks)
# Get middle point between thumb and ring finger for tracking
if is_scroll_gesture:
thumb_tip = landmarks[mp_hands.HandLandmark.THUMB_TIP]
ring_tip = landmarks[mp_hands.HandLandmark.RING_FINGER_TIP]
current_y = (thumb_tip.y + ring_tip.y) / 2
# Initialize scroll if just started pinching
if not scroll_active:
scroll_active = True
scroll_start_y = current_y
else:
# Calculate scroll distance
current_time = time.time()
if current_time - last_scroll_time > scroll_cooldown:
# Convert movement to scroll amount
scroll_amount = int((current_y - scroll_start_y) * 20 * scroll_sensitivity)
if abs(scroll_amount) > 0:
# Scroll up or down
pyautogui.scroll(-scroll_amount) # Negative because screen coordinates are inverted
scroll_start_y = current_y # Reset start position
last_scroll_time = current_time
else:
scroll_active = False
This implementation:
- Detects a pinch between the thumb and ring finger
- Tracks the vertical movement of the pinch
- Converts the movement to scrolling actions
- Uses a cooldown mechanism to prevent too many scroll events
- Applies sensitivity settings to adjust scroll speed
2. Alternative: Two-Finger Scroll Gesture
For users who might find the pinch gesture challenging, we can implement an alternative two-finger scroll method:
def detect_two_finger_scroll(landmarks):
"""Detect index and middle finger extended for scrolling"""
index_tip = landmarks[mp_hands.HandLandmark.INDEX_FINGER_TIP]
index_pip = landmarks[mp_hands.HandLandmark.INDEX_FINGER_PIP]
middle_tip = landmarks[mp_hands.HandLandmark.MIDDLE_FINGER_TIP]
middle_pip = landmarks[mp_hands.HandLandmark.MIDDLE_FINGER_PIP]
# Check if both fingers are extended (tips above pips)
index_extended = index_tip.y < index_pip.y
middle_extended = middle_tip.y < middle_pip.y
# Check if other fingers are curled
ring_tip = landmarks[mp_hands.HandLandmark.RING_FINGER_TIP]
ring_pip = landmarks[mp_hands.HandLandmark.RING_FINGER_PIP]
pinky_tip = landmarks[mp_hands.HandLandmark.PINKY_TIP]
pinky_pip = landmarks[mp_hands.HandLandmark.PINKY_PIP]
ring_curled = ring_tip.y > ring_pip.y
pinky_curled = pinky_tip.y > pinky_pip.y
# Return true if index and middle extended, others curled
return index_extended and middle_extended and ring_curled and pinky_curled
This can then be integrated into the main loop similarly to the pinch gesture method.
3. Visual Feedback for Scrolling
Providing visual feedback helps users understand when the system recognizes their scroll gesture:
# Inside the main loop, when scroll gesture is detected:
if is_scroll_gesture:
# Draw a visual indicator for active scrolling
cv2.circle(image, (50, 50), 20, (0, 255, 0), -1) # Green circle when scrolling
cv2.putText(image, f"Scrolling {'UP' if scroll_amount < 0 else 'DOWN'}",
(75, 50), cv2.FONT_HERSHEY_SIMPLEX, 0.7, (0, 255, 0), 2)
Adjustable Mouse Sensitivity
Different users have different preferences for cursor speed and precision. Let’s implement adjustable sensitivity controls:
1. Adding Sensitivity Settings
First, we’ll define sensitivity parameters that can be adjusted:
# Mouse movement sensitivity settings
mouse_sensitivity = 1.0 # Default value
sensitivity_min = 0.2 # Minimum allowed sensitivity
sensitivity_max = 3.0 # Maximum allowed sensitivity
sensitivity_step = 0.1 # Increment/decrement step
2. Applying Sensitivity to Mouse Movement
We need to modify our mouse movement logic to incorporate the sensitivity setting:
# Inside the main loop, when calculating cursor position:
wrist = landmarks[mp_hands.HandLandmark.WRIST]
# Get raw coordinates
raw_x = wrist.x * screen_width
raw_y = wrist.y * screen_height
# Calculate center of screen
center_x = screen_width / 2
center_y = screen_height / 2
# Apply sensitivity to the distance from center
offset_x = (raw_x - center_x) * mouse_sensitivity
offset_y = (raw_y - center_y) * mouse_sensitivity
# Calculate final position
x = int(center_x + offset_x)
y = int(center_y + offset_y)
# Apply smoothing for stable cursor movement
prev_x = prev_x + (x - prev_x) / smoothing
prev_y = prev_y + (y - prev_y) / smoothing
# Move the mouse
pyautogui.moveTo(prev_x, prev_y)
This approach:
- Calculates the cursor position relative to the center of the screen
- Applies the sensitivity factor to the offset from center
- Ensures that low sensitivity gives fine control, while high sensitivity allows rapid movement across the screen
3. Gesture-Based Sensitivity Adjustment
Now we’ll implement gestures to adjust sensitivity on-the-fly:
# Global variables for tracking the last sensitivity adjustment
last_sensitivity_change_time = 0
sensitivity_change_cooldown = 1.0 # Seconds between adjustments
def detect_increase_sensitivity_gesture(landmarks):
"""Detect gesture for increasing sensitivity (pinky and thumb pinch)"""
thumb_tip = landmarks[mp_hands.HandLandmark.THUMB_TIP]
pinky_tip = landmarks[mp_hands.HandLandmark.PINKY_TIP]
distance = np.sqrt((thumb_tip.x - pinky_tip.x)**2 + (thumb_tip.y - pinky_tip.y)**2)
return distance < 0.07
def detect_decrease_sensitivity_gesture(landmarks):
"""Detect gesture for decreasing sensitivity (thumb touching wrist)"""
thumb_tip = landmarks[mp_hands.HandLandmark.THUMB_TIP]
wrist = landmarks[mp_hands.HandLandmark.WRIST]
distance = np.sqrt((thumb_tip.x - wrist.x)**2 + (thumb_tip.y - wrist.y)**2)
return distance < 0.12
# In the main loop:
# Check for sensitivity adjustment gestures
current_time = time.time()
if current_time - last_sensitivity_change_time > sensitivity_change_cooldown:
if detect_increase_sensitivity_gesture(landmarks):
mouse_sensitivity = min(mouse_sensitivity + sensitivity_step, sensitivity_max)
print(f"Sensitivity increased to: {mouse_sensitivity:.1f}")
last_sensitivity_change_time = current_time
elif detect_decrease_sensitivity_gesture(landmarks):
mouse_sensitivity = max(mouse_sensitivity - sensitivity_step, sensitivity_min)
print(f"Sensitivity decreased to: {mouse_sensitivity:.1f}")
last_sensitivity_change_time = current_time
4. On-Screen Sensitivity Display
To help users understand the current sensitivity level, we can display it on the screen:
# Inside the main loop, after handling sensitivity adjustments:
# Display current sensitivity on screen
cv2.putText(image, f"Sensitivity: {mouse_sensitivity:.1f}",
(10, image.shape[0] - 20), cv2.FONT_HERSHEY_SIMPLEX,
0.7, (0, 255, 0), 2)
5. UI Controls for Sensitivity Adjustment
For a more user-friendly experience, we can add GUI controls using OpenCV:
# Create a sensitivity slider using OpenCV
def create_control_window():
cv2.namedWindow('Mouse Controls')
cv2.createTrackbar('Sensitivity', 'Mouse Controls',
int(mouse_sensitivity * 10),
int(sensitivity_max * 10),
on_sensitivity_change)
cv2.createTrackbar('Scroll Speed', 'Mouse Controls',
int(scroll_sensitivity * 10),
int(sensitivity_max * 10),
on_scroll_sensitivity_change)
def on_sensitivity_change(value):
global mouse_sensitivity
mouse_sensitivity = value / 10.0
def on_scroll_sensitivity_change(value):
global scroll_sensitivity
scroll_sensitivity = value / 10.0
# Call at the beginning of your program
create_control_window()
6. Configuration File for Persistent Settings
To remember user preferences between sessions, we can save settings to a configuration file:
import json
import os
config_file = "gesture_mouse_config.json"
def save_settings():
"""Save current settings to a JSON file"""
settings = {
"mouse_sensitivity": mouse_sensitivity,
"scroll_sensitivity": scroll_sensitivity,
"smoothing": smoothing
}
with open(config_file, 'w') as f:
json.dump(settings, f)
print("Settings saved!")
def load_settings():
"""Load settings from a JSON file if it exists"""
global mouse_sensitivity, scroll_sensitivity, smoothing
if os.path.exists(config_file):
try:
with open(config_file, 'r') as f:
settings = json.load(f)
mouse_sensitivity = settings.get("mouse_sensitivity", mouse_sensitivity)
scroll_sensitivity = settings.get("scroll_sensitivity", scroll_sensitivity)
smoothing = settings.get("smoothing", smoothing)
print("Settings loaded!")
except:
print("Error loading settings. Using defaults.")
# Load settings at startup
load_settings()
# Add keyboard event to save settings:
# (inside the main loop)
key = cv2.waitKey(1) & 0xFF
if key == ord('s'):
save_settings()
Technical Challenges and Solutions
Challenge 1: Hand Detection Stability
Problem: Hand detection can be inconsistent under varying lighting conditions or when the hand moves quickly.
Solution: Multiple approaches can improve stability:
- Adjust MediaPipe confidence thresholds based on your environment
- Implement background removal techniques to isolate the hand
- Use temporal filtering to reject spurious detections
Challenge 2: Gesture Recognition Accuracy
Problem: Distinguishing intentional gestures from natural hand movements.
Solution:
- Define clear gesture thresholds
- Implement gesture “holding” requirements (e.g., maintain a gesture for 300ms)
- Add visual feedback to help users understand when gestures are recognized
Challenge 3: Cursor Stability
Problem: Direct mapping of hand position to cursor coordinates can result in jittery movement.
Solution:
- Implement motion smoothing algorithms (like our weighted average approach)
- Use Kalman filtering for more sophisticated motion prediction
- Create a “deadzone” where small hand movements don’t affect the cursor
Challenge 4: Fatigue and Ergonomics
Problem: Holding the hand in mid-air causes user fatigue over time.
Solution:
- Implement a “clutch” mechanism that enables/disables control
- Design gestures that allow for natural hand positions
- Consider relative positioning rather than absolute positioning
Challenge 5: Scroll Precision
Problem: Scrolling can be too sensitive or jerky with direct hand movement mapping.
Solution:
- Implement non-linear scroll response curves
- Add “scroll momentum” for smoother continuous scrolling
- Provide visual feedback about scroll speed and direction
# Non-linear scroll response curve
def apply_scroll_curve(movement):
"""Apply a non-linear curve to make small movements more precise"""
# Square the movement but keep the sign
sign = 1 if movement >= 0 else -1
magnitude = abs(movement)
# Apply curve: square for values > 0.1, linear for smaller values
if magnitude > 0.1:
result = sign * ((magnitude - 0.1) ** 2) * 2 + (sign * 0.1)
else:
result = sign * magnitude
return result
Advanced Features and Improvements
Enhancing Mouse Movement
For more precise control, we can improve the mapping between hand position and cursor movement:
# Define a region of interest in the camera's field of view
roi_left = 0.2
roi_right = 0.8
roi_top = 0.2
roi_bottom = 0.8
# Map the hand position within this region to screen coordinates
def map_to_screen(x, y):
screen_x = screen_width * (x - roi_left) / (roi_right - roi_left)
screen_y = screen_height * (y - roi_top) / (roi_bottom - roi_top)
return max(0, min(screen_width, screen_x)), max(0, min(screen_height, screen_y))
This approach creates a smaller “active area” within the camera’s view, allowing for more precise movements.
Implementing Additional Gestures
Beyond basic clicking, we can add more complex interactions:
- Scroll wheel emulation:
def detect_scroll_gesture(landmarks):
thumb_tip = landmarks[mp_hands.HandLandmark.THUMB_TIP]
index_tip = landmarks[mp_hands.HandLandmark.INDEX_FINGER_TIP]
# Calculate pinch distance
distance = ((thumb_tip.x - index_tip.x)**2 + (thumb_tip.y - index_tip.y)**2)**0.5
# If pinching, track vertical movement for scrolling
if distance < pinch_threshold:
return (index_tip.y - prev_index_y) * scroll_sensitivity
return 0
- Drag and drop:
# Track index finger extension status
index_extended = landmarks[mp_hands.HandLandmark.INDEX_FINGER_TIP].y < landmarks[mp_hands.HandLandmark.INDEX_FINGER_PIP].y
# If status changes from extended to not extended while moving, start drag
if prev_index_extended and not index_extended:
pyautogui.mouseDown()
elif not prev_index_extended and index_extended:
pyautogui.mouseUp()
- Gesture-based shortcuts:
# Detect specific finger configurations
if all_fingers_extended(landmarks):
# Perform action, like opening task manager
pyautogui.hotkey('ctrl', 'shift', 'esc')
Calibration System
A calibration system improves accuracy across different users and environments:
def calibrate():
calibration_points = [(0.1, 0.1), (0.9, 0.1), (0.9, 0.9), (0.1, 0.9)]
user_points = []
for point in calibration_points:
# Prompt user to place hand at this position
# Record actual hand position
user_points.append((wrist.x, wrist.y))
# Create transformation matrix
transformation = calculate_transformation(calibration_points, user_points)
return transformation
Performance Optimization
To ensure smooth operation, several optimizations are critical:
1. Frame Rate Management
Processing every frame can be computationally expensive. We can reduce the processing load:
# Process only every n frames
if frame_count % process_every_n_frames == 0:
# Process hand detection and tracking
else:
# Use the previous result
2. Resolution Scaling
Lower resolution processing can significantly improve performance:
# Scale down the image for processing
process_scale = 0.5
small_frame = cv2.resize(image, (0, 0), fx=process_scale, fy=process_scale)
# Process the smaller image
results = hands.process(small_frame)
# Scale coordinates back up when using them
x = int(landmark.x / process_scale)
y = int(landmark.y / process_scale)
3. Multi-threading
Separating video capture from processing improves responsiveness:
def capture_thread():
while running:
ret, frame = cap.read()
if ret:
frame_queue.put(frame)
def process_thread():
while running:
if not frame_queue.empty():
frame = frame_queue.get()
# Process the frame
Real-World Applications
Gesture control systems have numerous practical applications beyond cursor control:
- Accessibility: Enables computer use for people with mobility impairments
- Medical Environments: Allows for touchless interaction in sterile settings
- Presentations: Facilitates natural interaction with slides and content
- Gaming: Creates immersive control experiences without specialized hardware
- Smart Home Control: Enables intuitive interaction with IoT devices
- Virtual Reality: Provides hand tracking for more realistic VR experiences
Challenges and Future Directions
While powerful, gesture control systems face several ongoing challenges:
Technical Limitations
- Occlusion: Fingers may be hidden from the camera’s view
- Background Complexity: Busy environments can confuse hand detection
- Lighting Sensitivity: Performance varies with lighting conditions
- Camera Limitations: Low frame rates or resolution affect tracking quality
Future Research Directions
- Multi-modal Integration: Combining gestures with voice commands or eye tracking
- Context-aware Gestures: Adapting to different applications automatically
- Personalized Gestures: Learning user-specific gesture patterns
- Transfer Learning: Applying knowledge from one gesture domain to another
- Edge Processing: Moving computations to specialized hardware for better performance
Conclusion
Computer vision-based gesture control represents a significant step forward in human-computer interaction, offering a more natural and intuitive way to control computers. By leveraging libraries like MediaPipe and OpenCV, developers can now create sophisticated gesture recognition systems with relatively modest technical requirements.
Our gesture-controlled mouse system demonstrates the core principles of this technology, with additional features like scrolling and adjustable sensitivity making it truly practical for everyday use. The accessibility and customizability of such systems highlight the exciting possibilities at the intersection of computer vision, machine learning, and human-computer interaction.
Whether for accessibility, specialized environments, or simply for the joy of a more natural interaction, gesture control systems are poised to become an increasingly common part of our digital interfaces.
Code Repository
The complete implementation of the gesture-controlled mouse system described in this blog is available on GitHub at {https://github.com/tejask0512/Hand_Gesture_Mouse_Computer_Vision} . The code is extensively commented to help you understand each component and customize it for your specific needs.
References and Further Reading
- MediaPipe Hands: https://google.github.io/mediapipe/solutions/hands.html
- OpenCV Documentation: https://docs.opencv.org/
- PyAutoGUI Documentation: https://pyautogui.readthedocs.io/
- “Hand Gesture Recognition: A Literature Review” – S. S. Rautaray and A. Agrawal
- “Vision Based Hand Gesture Recognition for Human Computer Interaction” – Pavlovic et al.
Mapping Air Quality Index: A Deep Dive into the AQI Google Maps Project
In an era where environmental concerns increasingly shape public policy and personal health decisions, access to real-time air quality data has never been more crucial. The AQI Google Maps project represents an innovative approach to environmental monitoring, combining Google Maps’ familiar interface with critical air quality metrics. This open-source initiative transforms complex environmental data into an accessible visualization tool that can benefit researchers, policymakers, and everyday citizens concerned about the air they breathe.
What is the AQI Google Maps Project?
The AQI (Air Quality Index) Google Maps project is an open-source web application that integrates air quality data with Google Maps to provide a visual representation of air pollution levels across different locations. Developed by Tejas K (GitHub: tejask0512), this project leverages modern web technologies and public APIs to create an interactive map where users can view air quality conditions with intuitive color-coded markers.
Technical Architecture
The project employs a straightforward yet effective technical stack:
- Frontend: HTML, CSS, JavaScript
- APIs: Google Maps API for mapping functionality, Air Quality APIs for pollution data
- Data Visualization: Custom markers and color-coding system
The core functionality revolves around fetching air quality data based on geographic coordinates and rendering this information as color-coded markers on the Google Maps interface. The colors transition from green (good air quality) through yellow and orange to red and purple (hazardous air quality), providing an immediate visual understanding of conditions in different areas.
Deep Dive into AQI Analysis
Understanding the Air Quality Index
The Air Quality Index is a standardized indicator developed by environmental agencies to communicate how polluted the air is and what associated health effects might be. The AQI Google Maps project implements this complex calculation system and presents it in an accessible format.
The AQI typically accounts for multiple pollutants:
| Pollutant | Source | Health Impact |
|---|---|---|
| PM2.5 (Fine Particulate Matter) | Combustion engines, forest fires, industrial processes | Can penetrate deep into lungs and bloodstream |
| PM10 (Coarse Particulate Matter) | Dust, pollen, mold | Respiratory irritation, asthma exacerbation |
| O3 (Ozone) | Created by chemical reactions between NOx and VOCs | Lung damage, respiratory issues |
| NO2 (Nitrogen Dioxide) | Vehicles, power plants | Respiratory inflammation |
| SO2 (Sulfur Dioxide) | Fossil fuel combustion, industrial processes | Respiratory issues, contributes to acid rain |
| CO (Carbon Monoxide) | Incomplete combustion | Reduces oxygen delivery in bloodstream |
The project likely calculates an overall AQI based on the highest concentration of any single pollutant, following the EPA’s approach where:
- 0-50 (Green): Good air quality with minimal health concerns
- 51-100 (Yellow): Moderate air quality; unusually sensitive individuals may experience issues
- 101-150 (Orange): Unhealthy for sensitive groups
- 151-200 (Red): Unhealthy for all groups
- 201-300 (Purple): Very unhealthy; may trigger health alerts
- 301+ (Maroon): Hazardous; serious health effects for entire population
The technical implementation likely includes conversion formulas to normalize different pollutant measurements to the same 0-500 AQI scale.
Real-time Data Processing
A key technical achievement of the project is its ability to process real-time air quality data. This involves:
- API Integration: Connecting to air quality data providers through RESTful APIs
- Data Parsing: Extracting relevant metrics from JSON/XML responses
- Coordinate Mapping: Associating pollution data with precise geographic coordinates
- Temporal Synchronization: Managing data freshness and update frequencies
The project handles these operations seamlessly in the background, presenting users with up-to-date information without exposing the complexity of the underlying data acquisition process.
Report Generation Capabilities
One of the project’s valuable features is its ability to generate comprehensive air quality reports. These reports serve multiple purposes:
Types of Reports Generated
- Location-specific Snapshots: Detailed breakdowns of current air quality at selected points
- Comparative Analysis: Contrasting air quality across multiple locations
- Temporal Reports: Tracking air quality changes over time (hourly, daily, weekly)
- Pollutant-specific Reports: Focusing on individual contaminants like PM2.5 or O3
Report Components
The reporting system likely includes:
- Statistical Summaries: Min/max/mean values for AQI metrics
- Health Impact Assessments: Explanations of potential health effects based on current readings
- Visualizations: Charts and graphs depicting pollution trends
- Contextual Information: Weather conditions that may influence readings
- Actionable Recommendations: Suggested activities based on air quality levels
Technical Implementation of Reporting
From a development perspective, the reporting functionality demonstrates sophisticated data processing:
// Conceptual example of report generation logic
function generateAQIReport(locationData, timeframe) {
const reportData = {
location: locationData.name,
coordinates: locationData.coordinates,
timestamp: new Date(),
metrics: {
overall: calculateOverallAQI(locationData.pollutants),
individual: locationData.pollutants,
trends: analyzeTrends(locationData.history, timeframe)
},
healthImplications: assessHealthImpact(calculateOverallAQI(locationData.pollutants)),
recommendations: generateRecommendations(calculateOverallAQI(locationData.pollutants))
};
return formatReport(reportData, preferredFormat);
}
This functionality transforms raw data into actionable intelligence, making the project valuable beyond simple visualization.
AQI and Location Coordinate Data for Machine Learning
Perhaps the most forward-looking aspect of the project is its potential for generating valuable datasets for machine learning applications. The combination of precise geolocation data with corresponding air quality metrics creates numerous possibilities for advanced environmental analysis.
Data Generation for ML Models
The project effectively creates a continuous stream of structured data points with these key attributes:
- Geographic Coordinates: Latitude and longitude
- Temporal Information: Timestamps for each measurement
- Multiple Pollutant Metrics: PM2.5, PM10, O3, NO2, SO2, CO values
- Calculated AQI: Overall air quality index
- Contextual Metadata: Potentially including weather conditions, urban density, etc.
This multi-dimensional dataset serves as excellent training data for various machine learning models.
Potential ML Applications
With sufficient data collection over time, the following machine learning approaches become possible:
1. Predictive Modeling
Machine learning algorithms can be trained to forecast air quality based on historical patterns:
- Time Series Forecasting: Using techniques like ARIMA, LSTM networks, or Prophet to predict AQI values hours or days in advance
- Multivariate Prediction: Incorporating weather forecasts, traffic patterns, and seasonal factors to improve accuracy
- Anomaly Detection: Identifying unusual pollution events that deviate from expected patterns
# Conceptual example of LSTM model for AQI prediction
from keras.models import Sequential
from keras.layers import LSTM, Dense
def build_aqi_prediction_model(lookback_window):
model = Sequential()
model.add(LSTM(50, activation='relu', input_shape=(lookback_window, n_features)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')
return model
# Train with historical AQI data from project
model = build_aqi_prediction_model(24) # 24-hour lookback window
model.fit(X_train, y_train, epochs=100, validation_split=0.2)
2. Spatial Analysis and Interpolation
The geospatial nature of the data enables sophisticated spatial modeling:
- Kriging/Gaussian Process Regression: Estimating pollution levels between measurement points
- Spatial Autocorrelation: Analyzing how pollution levels at one location influence nearby areas
- Hotspot Identification: Using clustering algorithms to detect persistent pollution sources
# Conceptual example of spatial interpolation
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel
def interpolate_aqi_surface(known_points, known_values, grid_points):
# Define kernel - distance matters for pollution spread
kernel = RBF(length_scale=1.0) + WhiteKernel(noise_level=0.1)
gpr = GaussianProcessRegressor(kernel=kernel)
# Train on known AQI points
gpr.fit(known_points, known_values)
# Predict AQI at all grid points
predicted_values = gpr.predict(grid_points)
return predicted_values
3. Causal Analysis
Advanced machine learning techniques can help identify pollution drivers:
- Causal Inference Models: Determining the impact of traffic changes, industrial activities, or policy interventions on air quality
- Counterfactual Analysis: Estimating what air quality would be under different conditions
- Attribution Modeling: Quantifying the contribution of different sources to overall pollution levels
4. Computer Vision Integration
The project’s map-based approach opens possibilities for combining with visual data:
- Satellite Imagery Analysis: Correlating visible pollution (smog, industrial activity) with measured AQI
- Traffic Density Estimation: Using traffic camera feeds to predict localized pollution spikes
- Urban Development Impact: Analyzing how changes in urban landscapes affect air quality patterns
Implementation Considerations for ML Integration
To fully realize the machine learning potential, the project could implement:
- Data Export APIs: Programmatic access to historical AQI and coordinate data
- Standardized Dataset Generation: Creating properly formatted, cleaned datasets ready for ML models
- Feature Engineering Utilities: Tools to extract temporal patterns, spatial relationships, and other derived features
- Model Integration Endpoints: APIs that allow trained models to feed predictions back into the visualization system
// Conceptual implementation of data export for ML
function exportTrainingData(startDate, endDate, region, format='csv') {
const dataPoints = fetchHistoricalData(startDate, endDate, region);
// Process for ML readiness
const mlReadyData = dataPoints.map(point => ({
timestamp: point.timestamp,
lat: point.coordinates.lat,
lng: point.coordinates.lng,
pm25: point.pollutants.pm25,
pm10: point.pollutants.pm10,
o3: point.pollutants.o3,
no2: point.pollutants.no2,
so2: point.pollutants.so2,
co: point.pollutants.co,
aqi: point.aqi,
// Derived features
hour_of_day: new Date(point.timestamp).getHours(),
day_of_week: new Date(point.timestamp).getDay(),
is_weekend: [0, 6].includes(new Date(point.timestamp).getDay()),
season: calculateSeason(point.timestamp)
}));
return formatDataForExport(mlReadyData, format);
}
Key Features and Capabilities
The project demonstrates several notable features:
- Real-time air quality visualization: Displays current AQI values at selected locations
- Interactive map interface: Users can navigate, zoom, and click on markers to view detailed information
- Color-coded AQI indicators: Intuitive visual representation of pollution levels
- Customizable markers: Location-specific information about air quality conditions
- Responsive design: Functions across various device types and screen sizes
Environmental and Health Significance
The importance of this project extends far beyond its technical implementation. Here’s why such tools matter:
Public Health Impact
Air pollution is directly linked to numerous health problems, including respiratory diseases, cardiovascular issues, and even neurological disorders. According to the World Health Organization, air pollution causes approximately 7 million premature deaths annually worldwide. By making air quality data more accessible, this project empowers individuals to:
- Make informed decisions about outdoor activities
- Understand when to take protective measures (like wearing masks or staying indoors)
- Recognize patterns in local air quality that might affect their health
Environmental Awareness
Environmental literacy begins with awareness. When people can visually connect with environmental data, they’re more likely to:
- Understand the scope and severity of air pollution issues
- Recognize temporal and spatial patterns in air quality
- Connect human activities with environmental outcomes
- Support policies aimed at improving air quality
Research and Policy Applications
For researchers and policymakers, visualized air quality data offers valuable insights:
- Identifying pollution hotspots that require intervention
- Evaluating the effectiveness of environmental regulations
- Planning urban development with air quality considerations
- Allocating resources for environmental monitoring and mitigation
Case Study: Urban Planning and Environmental Justice
The AQI Google Maps project provides a powerful tool for addressing environmental justice concerns. By visualizing pollution patterns across different neighborhoods, it can reveal disparities in air quality that often correlate with socioeconomic factors.
Data-Driven Environmental Justice
Researchers can use the generated datasets to:
- Identify Disproportionate Impacts: Quantify differences in air quality across neighborhoods with varying income levels or racial demographics
- Temporal Justice Analysis: Determine if certain communities bear the burden of poor air quality during specific times (e.g., industrial activity hours)
- Policy Effectiveness: Measure how environmental regulations impact different communities
Practical Application Example
Consider a city planning department using the AQI Google Maps project to assess the impact of a proposed industrial development:
- Establish baseline air quality readings across all affected neighborhoods
- Use predictive modeling (with the ML techniques described above) to estimate pollution changes
- Generate reports showing projected AQI impacts on different communities
- Adjust development plans to minimize disproportionate impacts on vulnerable populations
This data-driven approach promotes equitable development and environmental protection.
The Future of Environmental Data Integration
The AQI Google Maps project represents an important step toward more integrated environmental monitoring. Future development could include:
Data Fusion Opportunities
- Cross-Pollutant Analysis: Investigating relationships between different pollutants
- Multi-Environmental Factor Integration: Combining air quality with noise pollution, water quality, and urban heat island effects
- Health Data Correlation: Connecting real-time AQI with emergency room visits for respiratory issues
Technical Evolution
- Edge Computing Integration: Processing air quality data from low-cost sensors at the edge
- Blockchain for Data Integrity: Ensuring the provenance and authenticity of environmental measurements
- Federated Learning: Enabling distributed model training across multiple air quality monitoring networks
Conclusion
The AQI Google Maps project represents an important intersection of environmental monitoring, data visualization, and public information. Its ability to generate structured air quality data associated with precise geographic coordinates creates a foundation for sophisticated analysis and machine learning applications.
By democratizing access to environmental data and creating opportunities for advanced computational analysis, this project contributes to both public awareness and scientific advancement. The potential for machine learning integration further elevates its significance, enabling predictive capabilities and deeper insights into pollution patterns.
As we continue to face environmental challenges, projects like this demonstrate how technology can be leveraged not just for convenience or entertainment, but for creating a more informed and environmentally conscious society. The combination of visual accessibility with data generation for machine learning represents a powerful approach to environmental monitoring that can drive both individual awareness and systemic change.
This blog post analyzes the AQI Google Maps project developed by Tejas K. The project is open-source and available for contributions on GitHub.

RegEx Mastery: Unlocking Structured Data From Unstructured Text
A comprehensive guide to advanced regular expressions for data mining and extraction
Introduction
In today’s data-driven world, the ability to efficiently extract structured information from unstructured text is invaluable. While many sophisticated NLP and machine learning tools exist for this purpose, regular expressions (regex) remain one of the most powerful and flexible tools in a data scientist’s toolkit. This blog explores advanced regex techniques implemented in the “Advance-Regex-For-Data-Mining-Extraction” project by Tejas K., demonstrating how carefully crafted patterns can transform raw text into actionable insights.
What Makes Regex Essential for Text Mining?
Regular expressions provide a concise, pattern-based approach to text processing that is:
- Language-agnostic: Works across programming languages and text processing tools
- Highly efficient: Once optimized, regex patterns can process large volumes of text quickly
- Precisely targeted: Allows extraction of exactly the information you need
- Flexible: Can be adapted to handle variations in text structure and format
Core Advanced Regex Techniques
Lookahead and Lookbehind Assertions
Lookahead (?=) and lookbehind (?<=) assertions are powerful techniques that allow matching patterns based on context without including that context in the match itself.
(?<=Price: \$)\d+\.\d{2}
This pattern matches a price value but only if it’s preceded by “Price: $”, without including “Price: $” in the match.
Non-Capturing Groups
When you need to group parts of a pattern but don’t need to extract that specific group:
(?:https?|ftp):\/\/[\w\.-]+\.[\w\.-]+
The ?: tells the regex engine not to store the protocol match (http, https, or ftp), improving performance.
Named Capture Groups
Named capture groups make your regex more readable and the extracted data more easily accessible:
(?<date>\d{2}-\d{2}-\d{4}).*?(?<email>[a-zA-Z0-9._%+-]+@[a-zA-Z0-9.-]+\.[a-zA-Z]{2,})
Instead of working with numbered groups, you can now reference the extractions by name: date and email.
Balancing Groups for Nested Structures
The project implements sophisticated balancing groups for parsing nested structures like JSON or HTML:
\{(?<open>\{)|(?<-open>\})|[^{}]*\}(?(open)(?!))
This pattern matches properly nested curly braces, essential for parsing structured data formats.
Real-World Applications in the Project
1. Extracting Structured Information from Resumes
The project demonstrates how to parse unstructured resume text to extract:
Education: (?<education>(?:(?!Experience|Skills).)+)
Experience: (?<experience>(?:(?!Education|Skills).)+)
Skills: (?<skills>.+)
This pattern breaks a resume into logical sections, making it possible to analyze each component separately.
2. Mining Financial Data from Reports
Annual reports and financial statements contain valuable data that can be extracted with patterns like:
Revenue of \$(?<revenue>[\d,]+(?:\.\d+)?) million in (?<year>\d{4})
This extracts both the revenue figure and the corresponding year in a single operation.
3. Processing Log Files
The project includes patterns for parsing common log formats:
(?<ip>\d{1,3}\.\d{1,3}\.\d{1,3}\.\d{1,3}) - - \[(?<datetime>[^\]]+)\] "(?<request>[^"]*)" (?<status>\d+) (?<size>\d+)
This extracts IP addresses, timestamps, request details, status codes, and response sizes from standard HTTP logs.
Performance Optimization Techniques
1. Catastrophic Backtracking Prevention
The project implements strategies to avoid catastrophic backtracking, which can cause regex operations to hang:
# Instead of this (vulnerable to backtracking)
(\w+\s+){1,5}
# Use this (prevents backtracking issues)
(?:\w+\s+){1,5}?
2. Atomic Grouping
Atomic groups improve performance by preventing unnecessary backtracking:
(?>https?://[\w-]+(\.[\w-]+)+)
Once the atomic group matches, the regex engine doesn’t try alternative ways to match it.
3. Strategic Anchoring
Using anchors strategically improves performance by limiting where the regex engine needs to look:
^Subject: (.+)$
By anchoring to line start/end, the engine only attempts matches at line boundaries.
Implementation in Python
The project primarily uses Python’s re module for implementation:
import re
def extract_structured_data(text):
pattern = r'Name: (?P<name>[\w\s]+)\s+Email: (?P<email>[^\s]+)\s+Phone: (?P<phone>[\d\-\(\)\s]+)'
match = re.search(pattern, text, re.MULTILINE)
if match:
return match.groupdict()
return None
For more complex operations, the project leverages the more powerful regex module which supports advanced features like recursive patterns:
import regex
def extract_nested_structures(text):
pattern = r'\((?:[^()]++|(?R))*+\)' # Recursive pattern for nested parentheses
matches = regex.findall(pattern, text)
return matches
Case Study: Extracting Product Information from E-commerce Text
One compelling example from the project is extracting product details from unstructured e-commerce descriptions:
Product: Premium Bluetooth Headphones XC-400
SKU: BT-400-BLK
Price: $149.99
Available Colors: Black, Silver, Blue
Features: Noise Cancellation, 30-hour Battery, Water Resistant
Using this regex pattern:
Product: (?<product>.+?)[\r\n]+
SKU: (?<sku>[A-Z0-9\-]+)[\r\n]+
Price: \$(?<price>\d+\.\d{2})[\r\n]+
Available Colors: (?<colors>.+?)[\r\n]+
Features: (?<features>.+)
The code extracts a structured object:
{
"product": "Premium Bluetooth Headphones XC-400",
"sku": "BT-400-BLK",
"price": "149.99",
"colors": "Black, Silver, Blue",
"features": "Noise Cancellation, 30-hour Battery, Water Resistant"
}
Best Practices and Lessons Learned
The project emphasizes several best practices for regex-based data extraction:
- Test with diverse data: Ensure your patterns work with various text formats and edge cases
- Document complex patterns: Add comments explaining the logic behind complex regex
- Break complex patterns into components: Build and test incrementally
- Balance precision and flexibility: Overly specific patterns may break with slight text variations
- Consider preprocessing: Sometimes cleaning text before applying regex yields better results
Future Directions
The “Advance-Regex-For-Data-Mining-Extraction” project continues to evolve with plans to:
- Implement more domain-specific extraction patterns for legal, medical, and technical texts
- Create a pattern library organized by text type and extraction target
- Develop a visual pattern builder to make complex regex more accessible
- Benchmark performance against machine learning approaches for similar extraction tasks
Conclusion
Regular expressions remain a remarkably powerful tool for text mining and data extraction. The techniques demonstrated in this project show how advanced regex can transform unstructured text into structured, analyzable data with precision and efficiency. While newer technologies like NLP models and machine learning techniques offer alternative approaches, the flexibility, speed, and precision of well-crafted regex patterns ensure they’ll remain relevant for data mining tasks well into the future.
By mastering the advanced techniques outlined in this blog post, you’ll be well-equipped to tackle complex text mining challenges and extract meaningful insights from the vast sea of unstructured text data that surrounds us.
This blog post explores the techniques implemented in the Advance-Regex-For-Data-Mining-Extraction project by Tejas K.

Predicting Forest Fires: A Deep Dive into the Algerian Forest Fire ML Project
In an era of climate change and increasing environmental challenges, forest fires have emerged as a critical concern with devastating ecological and economic impacts. The Algerian Forest Fire ML project represents an innovative application of machine learning techniques to predict fire occurrences in forest regions of Algeria. By leveraging data science, cloud computing, and predictive modeling, this open-source initiative creates a powerful tool that could help in early warning systems and resource allocation for fire prevention and management.
Project Overview
The Algerian Forest Fire ML project is a comprehensive machine learning application developed by Tejas K (GitHub: tejask0512) that focuses on predicting forest fire occurrences based on meteorological data and other environmental factors. Deployed as a cloud-based application, this project demonstrates how data science can be applied to critical environmental challenges.
Technical Architecture
The project employs a robust technical stack designed for accuracy, scalability, and accessibility:
- Programming Language: Python
- ML Frameworks: Scikit-learn for modeling, Pandas and NumPy for data manipulation
- Web Framework: Flask for API development
- Frontend: HTML, CSS, JavaScript
- Deployment: Cloud-based deployment (likely AWS, Azure, or similar platforms)
- Version Control: Git/GitHub
The architecture follows a classic machine learning pipeline pattern:
- Data ingestion and preprocessing
- Feature engineering and selection
- Model training and evaluation
- Model deployment as a web service
- User interface for prediction input and result visualization
Dataset Analysis
At the heart of the project is the Algerian Forest Fires dataset, which contains records of fires in the Bejaia and Sidi Bel-abbes regions of Algeria. The dataset includes various meteorological measurements and derived indices that are critical for fire prediction:
Key Features in the Dataset
| Feature | Description | Relevance to Fire Prediction |
|---|---|---|
| Temperature | Ambient temperature (°C) | Higher temperatures increase fire risk |
| Relative Humidity (RH) | Percentage of moisture in air | Lower humidity leads to drier conditions favorable for fires |
| Wind Speed | Wind velocity (km/h) | Higher winds spread fires more rapidly |
| Rain | Precipitation amount (mm) | Rainfall reduces fire risk by increasing moisture |
| FFMC | Fine Fuel Moisture Code | Indicates moisture content of litter and fine fuels |
| DMC | Duff Moisture Code | Indicates moisture content of loosely compacted organic layers |
| DC | Drought Code | Indicates moisture content of deep, compact organic layers |
| ISI | Initial Spread Index | Represents potential fire spread rate |
| BUI | Buildup Index | Indicates total fuel available for combustion |
| FWI | Fire Weather Index | Overall fire intensity indicator |
The project demonstrates sophisticated data analysis techniques, including:
- Exploratory Data Analysis (EDA): Thorough examination of feature distributions, correlations, and relationships with fire occurrences
- Data Cleaning: Handling missing values, outliers, and inconsistencies
- Feature Engineering: Creating derived features that might enhance predictive power
- Statistical Analysis: Identifying significant patterns and trends in historical fire data
# Conceptual example of EDA in the project
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# Load dataset
df = pd.read_csv('Algerian_forest_fires_dataset.csv')
# Analyze correlations between features and fire occurrence
correlation_matrix = df.corr()
plt.figure(figsize=(12, 10))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm')
plt.title('Feature Correlation Matrix')
plt.savefig('correlation_heatmap.png')
# Analyze seasonal patterns
monthly_fires = df.groupby('month')['Fire'].sum()
plt.figure(figsize=(10, 6))
monthly_fires.plot(kind='bar')
plt.title('Fire Occurrences by Month')
plt.xlabel('Month')
plt.ylabel('Number of Fires')
plt.savefig('monthly_fire_distribution.png')
Machine Learning Model Development
The core of the project is its predictive modeling capability. Based on repository analysis, the project likely implements several machine learning algorithms to predict forest fire occurrence:
Model Selection and Evaluation
The project appears to experiment with multiple classification algorithms:
- Logistic Regression: A baseline model for binary classification
- Random Forest: Ensemble method well-suited for environmental data
- Support Vector Machines: Effective for complex decision boundaries
- Gradient Boosting: Advanced ensemble technique for improved accuracy
- Neural Networks: Potentially used for capturing complex non-linear relationships
Each model undergoes rigorous evaluation using metrics particularly relevant to fire prediction:
- Accuracy: Overall correctness of predictions
- Precision: Proportion of positive identifications that were actually correct
- Recall (Sensitivity): Proportion of actual positives correctly identified
- F1 Score: Harmonic mean of precision and recall
- ROC-AUC: Area under the Receiver Operating Characteristic curve
# Conceptual example of model training and evaluation
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix
# Prepare data
X = df.drop('Fire', axis=1)
y = df['Fire']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
# Train Random Forest model
rf_model = RandomForestClassifier(n_estimators=100, random_state=42)
rf_model.fit(X_train, y_train)
# Evaluate model
y_pred = rf_model.predict(X_test)
print(classification_report(y_test, y_pred))
# Visualize confusion matrix
cm = confusion_matrix(y_test, y_pred)
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.title('Confusion Matrix')
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.savefig('confusion_matrix.png')
# Feature importance analysis
feature_importance = pd.DataFrame({
'Feature': X.columns,
'Importance': rf_model.feature_importances_
}).sort_values('Importance', ascending=False)
plt.figure(figsize=(10, 8))
sns.barplot(x='Importance', y='Feature', data=feature_importance)
plt.title('Feature Importance for Fire Prediction')
plt.savefig('feature_importance.png')
Hyperparameter Tuning
To maximize model performance, the project implements hyperparameter optimization techniques:
- Grid Search: Systematic exploration of parameter combinations
- Cross-Validation: K-fold validation to ensure model generalizability
- Bayesian Optimization: Potentially used for more efficient parameter search
Model Interpretability
Understanding why a model makes certain predictions is crucial for environmental applications. The project likely incorporates:
- Feature Importance Analysis: Identifying which meteorological factors most strongly influence fire predictions
- Partial Dependence Plots: Visualizing how each feature affects prediction outcomes
- SHAP (SHapley Additive exPlanations): Providing consistent and locally accurate explanations for model predictions
Cloud Deployment Architecture
A distinguishing aspect of this project is its cloud deployment strategy, making the predictive model accessible as a web service:
Deployment Components
- Model Serialization: Saving trained models using frameworks like Pickle or Joblib
- Flask API Development: Creating RESTful endpoints for prediction requests
- Web Interface: Building an intuitive interface for data input and result visualization
- Cloud Infrastructure: Deploying on scalable cloud platforms with considerations for:
- Computational scalability
- Storage requirements
- API request handling
- Security considerations
# Conceptual example of Flask API implementation
from flask import Flask, request, jsonify, render_template
import pickle
import numpy as np
app = Flask(__name__)
# Load the trained model
model = pickle.load(open('forest_fire_model.pkl', 'rb'))
@app.route('/')
def home():
return render_template('index.html')
@app.route('/predict', methods=['POST'])
def predict():
# Get input features from request
features = [float(x) for x in request.form.values()]
final_features = [np.array(features)]
# Make prediction
prediction = model.predict(final_features)
output = round(prediction[0], 2)
# Return prediction result
return render_template('index.html', prediction_text='Fire Risk: {}'.format(
'High' if output == 1 else 'Low'))
if __name__ == '__main__':
app.run(debug=True)
CI/CD Pipeline Integration
The project likely implements continuous integration and deployment practices:
- Automated Testing: Ensuring model performance and API functionality
- Version Control Integration: Tracking changes and coordinating development
- Containerization: Possibly using Docker for consistent deployment environments
- Infrastructure as Code: Defining cloud resources programmatically
Advanced Analytics and Reporting
Beyond basic prediction, the project implements sophisticated reporting capabilities:
Prediction Confidence Metrics
The system likely provides confidence scores with predictions, helping decision-makers understand reliability:
# Conceptual example of prediction with confidence
def predict_with_confidence(model, input_features):
# Get prediction probabilities
probabilities = model.predict_proba([input_features])[0]
# Determine prediction and confidence
prediction = 1 if probabilities[1] > 0.5 else 0
confidence = probabilities[1] if prediction == 1 else probabilities[0]
return {
'prediction': 'Fire Risk' if prediction == 1 else 'No Fire Risk',
'confidence': round(confidence * 100, 2),
'probability_distribution': {
'no_fire': round(probabilities[0] * 100, 2),
'fire': round(probabilities[1] * 100, 2)
}
}
Risk Level Classification
Rather than simple binary predictions, the system may implement risk stratification:
- Low Risk: Minimal fire danger, normal operations
- Moderate Risk: Increased vigilance recommended
- High Risk: Preventive measures advised
- Extreme Risk: Immediate action required
Visualization Components
The web interface likely includes data visualization tools:
- Risk Heatmaps: Geographic representation of fire risk levels
- Time Series Forecasting: Projecting risk levels over coming days
- Factor Contribution Charts: Showing how each meteorological factor contributes to current risk
Environmental and Social Impact
The significance of this project extends far beyond its technical implementation:
Ecological Benefits
- Early Warning System: Providing advance notice of high-risk conditions
- Resource Optimization: Helping authorities allocate firefighting resources efficiently
- Habitat Protection: Minimizing damage to critical ecosystems
- Carbon Emission Reduction: Preventing the massive carbon release from forest fires
Economic Impact
Forest fires cause billions in damages annually. This predictive system could:
- Reduce Property Damage: Through early intervention and prevention
- Lower Firefighting Costs: By enabling more strategic resource allocation
- Protect Agricultural Resources: Safeguarding farms and livestock near forests
- Preserve Tourism Value: Maintaining the economic value of forest regions
Public Safety Enhancement
The project has clear implications for public safety:
- Population Warning Systems: Alerting communities at risk
- Evacuation Planning: Providing data for decision-makers managing evacuations
- Air Quality Management: Predicting smoke dispersion and health impacts
- Infrastructure Protection: Safeguarding critical infrastructure from fire damage
Machine Learning Approaches for Environmental Modeling
The Algerian Forest Fire ML project demonstrates several advanced machine learning techniques particularly suited to environmental applications:
Time Series Analysis
Forest fire risk has strong temporal components, and the project likely implements:
- Seasonal Decomposition: Identifying cyclical patterns in fire occurrence
- Autocorrelation Analysis: Understanding how past conditions influence current risk
- Time-based Feature Engineering: Creating lag variables and rolling statistics
# Conceptual example of time series feature engineering
def create_time_features(df):
# Create copy of dataframe
df_new = df.copy()
# Sort by date
df_new = df_new.sort_values('date')
# Create lag features for temperature
df_new['temp_lag_1'] = df_new['Temperature'].shift(1)
df_new['temp_lag_2'] = df_new['Temperature'].shift(2)
df_new['temp_lag_3'] = df_new['Temperature'].shift(3)
# Create rolling average features
df_new['temp_rolling_3'] = df_new['Temperature'].rolling(window=3).mean()
df_new['humidity_rolling_3'] = df_new['RH'].rolling(window=3).mean()
# Create rate of change features
df_new['temp_roc'] = df_new['Temperature'].diff()
df_new['humidity_roc'] = df_new['RH'].diff()
# Drop rows with NaN values from feature creation
df_new = df_new.dropna()
return df_new
Transfer Learning Opportunities
The project methodology could potentially be transferred to other regions:
- Model Adaptation: Adjusting the model for different forest types and climates
- Domain Adaptation: Techniques to apply Algerian models to other countries
- Knowledge Transfer: Sharing insights about feature importance across regions
Ensemble Approaches
Given the critical nature of fire prediction, the project likely employs ensemble techniques:
- Model Stacking: Combining predictions from multiple algorithms
- Bagging and Boosting: Improving prediction stability and accuracy
- Weighted Voting: Giving more influence to models that perform better in specific conditions
# Conceptual example of ensemble model implementation
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
# Create base models
log_reg = LogisticRegression()
rf_clf = RandomForestClassifier()
svm_clf = SVC(probability=True)
# Create voting classifier
ensemble_model = VotingClassifier(
estimators=[
('lr', log_reg),
('rf', rf_clf),
('svc', svm_clf)
],
voting='soft' # Use predicted probabilities for voting
)
# Train ensemble model
ensemble_model.fit(X_train, y_train)
# Evaluate ensemble performance
ensemble_accuracy = ensemble_model.score(X_test, y_test)
print(f"Ensemble Model Accuracy: {ensemble_accuracy:.4f}")
Future Development Potential
The project contains significant potential for expansion:
Integration with Remote Sensing Data
Future versions could incorporate satellite imagery:
- Vegetation Indices: NDVI (Normalized Difference Vegetation Index) to assess fuel availability
- Thermal Anomaly Detection: Identifying hotspots from thermal sensors
- Smoke Detection: Early detection of fires through smoke signature analysis
Real-time Data Integration
Enhancing the system with real-time data feeds:
- Weather API Integration: Live meteorological data
- IoT Sensor Networks: Ground-based temperature, humidity, and wind sensors
- Drone Surveillance: Aerial monitoring of high-risk areas
Advanced Predictive Capabilities
Evolving beyond current predictive methods:
- Spatio-temporal Models: Predicting not just if, but where and when fires might occur
- Deep Learning Integration: Using CNNs or RNNs for more complex pattern recognition
- Reinforcement Learning: Optimizing resource allocation strategies for fire prevention
# Conceptual example of a more advanced deep learning approach
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense, Dropout
# Create LSTM model for time series prediction
def build_lstm_model(input_shape):
model = Sequential()
model.add(LSTM(64, return_sequences=True, input_shape=input_shape))
model.add(Dropout(0.2))
model.add(LSTM(32))
model.add(Dropout(0.2))
model.add(Dense(16, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(
loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy']
)
return model
# Reshape data for LSTM (samples, time steps, features)
X_train_lstm = X_train.values.reshape((X_train.shape[0], 1, X_train.shape[1]))
X_test_lstm = X_test.values.reshape((X_test.shape[0], 1, X_test.shape[1]))
# Create and train model
lstm_model = build_lstm_model((1, X_train.shape[1]))
lstm_model.fit(
X_train_lstm, y_train,
epochs=50,
batch_size=32,
validation_split=0.2
)
Climate Change Relevance
This project has particular significance in the context of climate change:
Climate Change Impact Assessment
- Long-term Trend Analysis: Evaluating how fire risk patterns are changing over decades
- Climate Scenario Modeling: Projecting fire risk under different climate change scenarios
- Adaptation Strategy Evaluation: Testing effectiveness of various preventive measures
Carbon Cycle Considerations
Forest fires are both influenced by and contribute to climate change:
- Carbon Release Estimation: Quantifying potential carbon emissions from predicted fires
- Ecosystem Recovery Modeling: Projecting how forests recover and sequester carbon after fires
- Climate Feedback Analysis: Understanding how increased fires may accelerate climate change
Conclusion
The Algerian Forest Fire ML project represents a powerful example of how data science and machine learning can address critical environmental challenges. By combining meteorological data analysis, advanced predictive modeling, and cloud-based deployment, this initiative creates a potentially life-saving tool for forest fire prediction and management.
The project’s significance extends beyond its technical implementation, offering real-world impact in ecological preservation, economic damage reduction, and public safety enhancement. As climate change increases the frequency and severity of forest fires globally, such predictive systems will become increasingly vital components of environmental management strategies.
For data scientists and environmental researchers, this project provides a valuable template for applying machine learning to ecological challenges. The methodology demonstrated could be adapted to various environmental prediction tasks, from drought forecasting to flood risk assessment.
As we continue to face growing environmental challenges, projects like the Algerian Forest Fire ML initiative showcase how technology can be harnessed not just for convenience or profit, but for protecting our natural resources and building more resilient communities.
This blog post analyzes the Algerian Forest Fire ML project developed by Tejas K. The project is open-source and available for contributions on GitHub.

AI and Blockchain Convergence & Transformers based Sentiment Analysis on Live Global News Data.
A Decentralized Autonomous Organization to Improve Coordination Between Nations Using Blockchain Technology, Artificial Intelligence and Natural Language Processing for Sentiment analysis on News Data.
- Client Tejas Kamble
- Date 29 April 2023
- Services AI & Blockchain Technology
Abstract
This paper is about Establishing a Decentralized organization with the Different Countries as members where all the countries will be considered as the node of the blockchain. All the countries in the organization will be treated equally there will not be any superpower amongst them. Therefore, The Organization will gather huge amount of the data from the different countries from all the sectors like health, education, economy, technology, culture, and agriculture which represents the overall development of the countries. All this gathered data will be further analyzed for their positive and negative impacts on all the mentioned sectors. This will give brief idea about situation of an individual country in different areas on that basis, members of the Organizations or we can say all the member countries will decide the reward or penalty case for the respective country. Blockchains have the potential to enhance systems by getting rid of middlemen. Artificial Intelligence will play a major role in this organization as dealing with massive amount of data will be in the frame and to deal with this data, we need AI to improve data integrity of the result which will be used by Smart-Contract for decision making purpose, automating, and optimizing the smart contract. AI promises to remove oversight and increase the objectivity of our systems. This organization offers a framework for participants to work together to create a dataset and host a model that is continuously updated using smart contracts. As data is growing rapidly. AI will manage that data efficiently with less energy consumption
Acceptance Letter 2

Research Blogs
The Complete Transformer Architecture: A Deep Dive
The Transformer architecture revolutionized natural language processing when it was introduced in the landmark 2017 paper “Attention Is All You Need” by Vaswani et al. This blog post explores the complete architecture, breaking down each component to provide a thorough understanding of how Transformers work.
Introduction
The Transformer model, introduced in the 2017 paper “Attention Is All You Need” by Vaswani et al., marked a pivotal shift in NLP architectures. Unlike recurrent neural networks (RNNs) and convolutional neural networks (CNNs), Transformers rely entirely on attention mechanisms, eliminating the need for recurrence and convolutions. This design allows for significantly more parallelization during training and has become the foundation for models like BERT, GPT, and T5.
Core Architecture
The Transformer follows an encoder-decoder architecture, but with a novel approach:
- Encoder: Processes the input sequence and builds representations
- Decoder: Generates output sequences using both the encoder’s representations and its own previous outputs
Both components are composed of stacks of identical layers, each with two main sub-layers:
- Multi-head attention mechanism
- Position-wise fully connected feed-forward network
Let’s break down each component in detail.
Encoder Architecture
The encoder consists of N identical layers (N=6 in the original paper). Each layer has two sub-layers:
1. Multi-Head Self-Attention
The first sub-layer is a multi-head self-attention mechanism. Self-attention allows the encoder to consider all positions in the input sequence when encoding a specific position, enabling the model to capture relationships regardless of their distance in the sequence.
The self-attention mechanism is calculated as follows:
- For each word in the input, three vectors are created:
- Query (Q): What the current word is looking for
- Key (K): What the current word contains
- Value (V): The actual content of the word
- For each position, scores are calculated using the query and key vectors:
Attention(Q, K, V) = softmax(QK^T / √dk) × V
The paper’s use of “scaled dot-product attention” introduces scaling by 1/√dk (where dk is the dimension of the key vectors) to prevent the softmax function from entering regions with extremely small gradients.
Multi-Head Attention
Rather than performing a single attention function, the Transformer uses multi-head attention:
MultiHead(Q, K, V) = Concat(head₁, head₂, ..., headₕ)W^O
where headᵢ = Attention(QW^Q_i, KW^K_i, VW^V_i)
In the original paper, they used h=8 parallel attention heads. Each head uses different learned linear projections for queries, keys, and values, allowing the model to jointly attend to information from different representation subspaces.
2. Position-wise Feed-Forward Network
The second sub-layer is a simple feed-forward network applied to each position separately and identically:
FFN(x) = max(0, xW₁ + b₁)W₂ + b₂
This is a two-layer neural network with a ReLU activation in between. In the original implementation, the inner layer has a dimensionality of 2048, while input and output are of dimension 512.
Residual Connections and Layer Normalization
Around each sub-layer, the encoder employs a residual connection followed by layer normalization:
LayerNorm(x + Sublayer(x))
This helps with training deeper networks and maintains gradient flow.
Decoder Architecture
The decoder also consists of N identical layers (N=6 in the original paper), but each decoder layer has three sub-layers:
1. Masked Multi-Head Self-Attention
The first sub-layer is similar to the encoder’s self-attention but includes a masking mechanism. This masking ensures that predictions for a position can only depend on known outputs at earlier positions, preserving the auto-regressive property needed during training.
2. Multi-Head Attention Over Encoder Output
The second sub-layer performs multi-head attention where:
- Queries (Q) come from the previous decoder layer
- Keys (K) and Values (V) come from the encoder’s output
This allows the decoder to focus on appropriate parts of the input sequence.
3. Position-wise Feed-Forward Network
The third sub-layer is identical to the feed-forward network used in the encoder.
Like the encoder, residual connections and layer normalization are applied around each sub-layer.
Embeddings and Positional Encoding
Input and Output Embeddings
Both the encoder and decoder use learned embeddings to convert input tokens to vectors of dimension d_model (512 in the original paper). The same weight matrix is shared between the input embedding layers and the pre-softmax linear transformation.
Positional Encoding
Since the Transformer contains no recurrence or convolution, it needs a way to understand the order of the sequence. The solution is adding “positional encodings” to the input embeddings:
PE(pos, 2i) = sin(pos/10000^(2i/d_model))
PE(pos, 2i+1) = cos(pos/10000^(2i/d_model))
Where pos is the position and i is the dimension. This function creates a unique pattern for each position, allowing the model to understand relative positions in the sequence.
Self-Attention in Detail
The self-attention mechanism is the core innovation of the Transformer. Let’s take a deeper look at how it works:
Let me continue with my detailed breakdown of the Transformer architecture.
Multi-Head Attention in Detail
Rather than performing a single attention function, the Transformer employs multi-head attention, which allows the model to jointly attend to information from different representation subspaces:
Training and Optimization
The Transformer model was trained using the Adam optimizer with the following parameters:
- Learning rate varying according to a formula: lr = d_model^(-0.5) * min(step_num^(-0.5), step_num * warmup_steps^(-1.5))
- β₁ = 0.9, β₂ = 0.98, ε = 10^(-9)
- Warmup_steps = 4000
Additional techniques used during training included:
- Residual dropout with rate 0.1
- Label smoothing with value ε_ls = 0.1
Why Self-Attention?
The paper outlines several advantages of self-attention over recurrent and convolutional layers:
- Computational complexity per layer: Self-attention has lower complexity when the sequence length is smaller than the representation dimensionality.
- Amount of computation that can be parallelized: Self-attention requires a fixed number of sequential operations (O(1)), whereas recurrent layers require O(n) sequential operations.
- Path length between long-range dependencies: Self-attention creates direct connections between any two positions, resulting in maximum path length O(1), while recurrent layers require O(n) steps.
This table compares the computational characteristics:
| Layer Type | Complexity per Layer | Sequential Operations | Maximum Path Length |
|---|---|---|---|
| Self-Attention | O(n²·d) | O(1) | O(1) |
| Recurrent | O(n·d²) | O(n) | O(n) |
| Convolutional | O(k·n·d²) | O(1) | O(log_k(n)) |
Cross-Attention Mechanism
In the decoder, the second attention layer performs cross-attention, which is a crucial bridge between encoder and decoder:
- Queries (Q) come from the previous decoder layer
- Keys (K) and Values (V) come from the encoder’s output
This architecture enables the decoder to focus on appropriate parts of the input sequence, creating a context-aware generation process.
The mathematical formulation is the same as self-attention:
CrossAttention(Q, K, V) = softmax(QK^T / √dk) × V
The difference lies in the source of Q, K, and V vectors.
Implementation Details
The original Transformer model had the following hyperparameters:
- Encoder and decoder each had N=6 identical layers
- d_model = 512 (dimensionality of embeddings)
- d_ff = 2048 (dimensionality of feed-forward layers)
- h = 8 (number of attention heads)
- d_k = d_v = 64 (dimensionality of keys and values)
- Dropout rate of 0.1 was applied to the output of each sub-layer and to embeddings and positional encodings
Ablation Studies from the Paper
The authors conducted several experiments to validate design choices:
- Varying model size: Performance improved with both d_model and d_ff
- Attention heads: They found that multiple attention heads were better than a single head
- Attention vs. relative position: They experimented with relative positional representations but found similar results
Applications and Extensions
Since its introduction, the Transformer architecture has been the foundation for numerous breakthrough models:
- BERT (Bidirectional Encoder Representations from Transformers): Uses only the encoder portion for bidirectional context understanding
- GPT (Generative Pre-trained Transformer): Uses only the decoder portion for autoregressive text generation
- T5 (Text-to-Text Transfer Transformer): Frames all NLP tasks as text-to-text problems
- Vision Transformer (ViT): Adapts Transformers for image classification by treating image patches as sequence tokens
Limitations and Challenges
Despite its success, the Transformer has some limitations:
- Quadratic complexity: The self-attention mechanism scales quadratically with sequence length, making it computationally expensive for very long sequences
- Positional encoding limitations: The fixed positional encodings may not capture position information as effectively as recurrent architectures
- Limited inductive bias: Without the sequential bias of RNNs or the spatial locality bias of CNNs, Transformers may require more data to learn patterns
Addressing the Complexity Issue
Several approaches have been proposed to address the quadratic complexity issue:
- Sparse Attention: Only attend to a subset of positions
- Linear Attention: Reformulate attention to achieve linear complexity
- Local Attention: Restrict attention to local neighborhoods
- Longformer/BigBird: Use a combination of local, global, and random attention patterns
Conclusion
The Transformer architecture represents a paradigm shift in sequence modeling. By replacing recurrence and convolutions with self-attention, it achieves state-of-the-art results while being more parallelizable and requiring fewer parameters. Its success has led to a new generation of pre-trained models that have pushed the boundaries of what’s possible in natural language processing and beyond.
The fundamental principles of the Transformer—self-attention, multi-head attention, and position-wise feed-forward networks—have proven to be remarkably versatile and effective across domains, cementing its place as one of the most significant architectural innovations in deep learning.
References
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2017). Attention is all you need. Advances in Neural Information Processing Systems, 30.
- Devlin, J., Chang, M. W., Lee, K., & Toutanova, K. (2018). BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805.
- Radford, A., Narasimhan, K., Salimans, T., & Sutskever, I. (2018). Improving language understanding by generative pre-training.
- Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S., Matena, M., Zhou, Y., Li, W., & Liu, P. J. (2020). Exploring the limits of transfer learning with a unified text-to-text transformer. Journal of Machine Learning Research, 21(140), 1-67.
- Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer, M., Heigold, G., Gelly, S., Uszkoreit, J., & Houlsby, N. (2020). An image is worth 16×16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929.
Deep Dive into Encoder-Decoder Architecture: Theory, Implementation and Applications
Introduction
The encoder-decoder architecture represents one of the most influential developments in deep learning, particularly for sequence-to-sequence tasks. This architecture has revolutionized machine translation, speech recognition, image captioning, and many other applications where input and output data have different structures or lengths.
In this blog post, we’ll explore:
- The fundamental concepts behind encoder-decoder architectures
- Detailed breakdown of encoder and decoder components
- Core mechanisms including attention
- Step-by-step implementations with PyTorch
- Architectural diagrams and visualizations
- Advanced variants and state-of-the-art applications
Table of Contents
- Fundamentals of Encoder-Decoder Architecture
- The Encoder: Deep Dive
- The Decoder: Deep Dive
- Attention Mechanisms
- Implementation: Neural Machine Translation
- Training and Inference
- Advanced Architectures
- Applications and Use Cases
- Best Practices and Optimization
- Conclusion
<a name=”fundamentals”></a>
1. Fundamentals of Encoder-Decoder Architecture
Basic Concept
At its core, the encoder-decoder architecture consists of two main components:
- Encoder: Processes the input sequence and compresses it into a context vector (or a set of vectors)
- Decoder: Takes the context vector and generates the output sequence
This design allows the model to map between sequences of different types or lengths – for example, a sentence in English to its translation in French, or an image to a descriptive caption.
The Information Flow
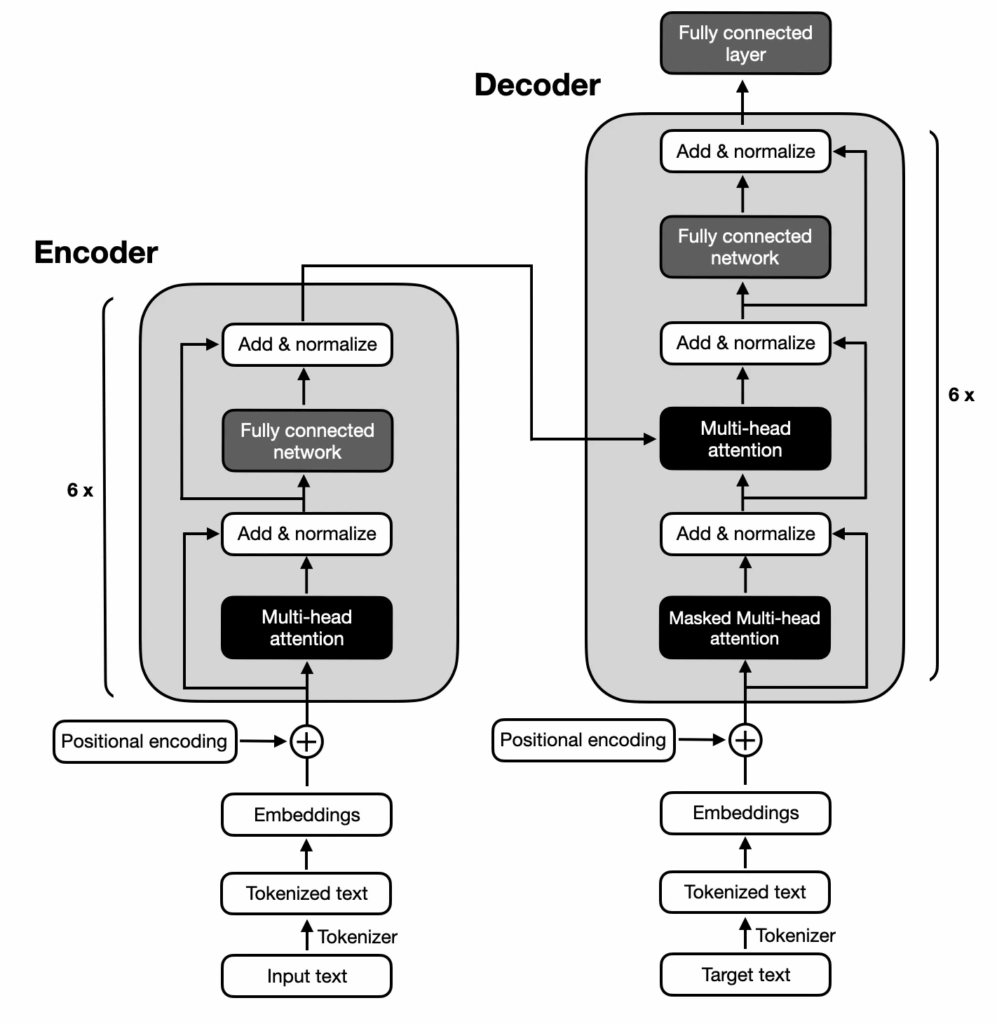
Input Sequence → Encoder → Context Vector(s) → Decoder → Output Sequence
Why Encoder-Decoder?
Traditional neural networks struggle with:
- Variable-length inputs and outputs
- Different dimensions between input and output spaces
- Preserving sequential relationships
The encoder-decoder architecture elegantly addresses these challenges by:
- Converting variable-length input into fixed-length representations
- Allowing different dimensionality in input and output
- Preserving sequence information through recurrent connections or attention
Main Variants
- RNN-based: Using LSTM or GRU cells for both encoder and decoder
- CNN-based: Using convolutional layers for encoding and sometimes decoding
- Transformer-based: Using self-attention mechanisms instead of recurrence
- Hybrid approaches: Combining different neural architectures
<a name=”encoder”></a>
2. The Encoder: Deep Dive
Purpose and Function
The encoder’s job is to process the input sequence and create a meaningful representation that captures its essential information. This representation should:
- Contain semantic information about the input
- Capture relationships between elements in the sequence
- Be in a form that the decoder can effectively use
Common Encoder Architectures
1. RNN-based Encoder
h₁ h₂ h₃ hₙ
↑ ↑ ↑ ↑
| | | |
┌─────┐ ┌─────┐ ┌─────┐ ┌─────┐
│ RNN │───│ RNN │───│ RNN │···│ RNN │
└─────┘ └─────┘ └─────┘ └─────┘
↑ ↑ ↑ ↑
x₁ x₂ x₃ xₙ
In an RNN encoder:
- Input tokens (x₁, x₂, …, xₙ) are processed sequentially
- Each RNN cell updates its hidden state based on the current input and previous hidden state
- The final hidden state (sometimes all hidden states) serves as the context vector
2. Bidirectional RNN Encoder
→→→→ Forward RNN →→→→
h₁← h₂← h₃← ... hₙ←
↑ ↑ ↑ ↑
x₁ x₂ x₃ ... xₙ
↓ ↓ ↓ ↓
h₁→ h₂→ h₃→ ... hₙ→
←←←← Backward RNN ←←←←
Bidirectional encoders:
- Process the sequence in both forward and backward directions
- Capture context from both past and future tokens
- Concatenate or combine both directions’ hidden states
3. Transformer Encoder
Multi-Head Self-Attention
↑
|
Add & Normalize
↑
|
Feed-Forward Neural Network
↑
|
Add & Normalize
↑
|
Positional Encoding
↑
|
Input Embedding
Transformer encoders:
- Process the entire sequence in parallel
- Use self-attention to model relationships between all positions
- Apply position encoding to maintain sequence order
- Stack multiple layers for deeper representations
Implementation of a Basic RNN Encoder
import torch
import torch.nn as nn
class EncoderRNN(nn.Module):
def __init__(self, input_size, hidden_size, embedding_size, num_layers=1, dropout=0.1):
"""
Arguments:
input_size: Size of vocabulary
hidden_size: Size of the hidden state
embedding_size: Size of the word embeddings
num_layers: Number of RNN layers
dropout: Dropout probability
"""
super(EncoderRNN, self).__init__()
self.hidden_size = hidden_size
self.num_layers = num_layers
# Word embedding layer
self.embedding = nn.Embedding(input_size, embedding_size)
# LSTM layer
self.lstm = nn.LSTM(
embedding_size,
hidden_size,
num_layers=num_layers,
bidirectional=True, # Using bidirectional LSTM
dropout=dropout if num_layers > 1 else 0,
batch_first=True
)
# Project bidirectional outputs to hidden_size
self.fc = nn.Linear(hidden_size * 2, hidden_size)
def forward(self, x, x_lengths):
"""
Arguments:
x: Input sequence tensor [batch_size, seq_len]
x_lengths: Length of each sequence in the batch
Returns:
outputs: All encoder hidden states [batch_size, seq_len, hidden_size]
hidden: Final encoder hidden state [num_layers*2, batch_size, hidden_size]
"""
batch_size = x.size(0)
# Create embedding
embedded = self.embedding(x) # [batch_size, seq_len, embedding_size]
# Pack padded sequence for efficient computation
packed = nn.utils.rnn.pack_padded_sequence(
embedded, x_lengths.cpu(), batch_first=True, enforce_sorted=False
)
# Forward through LSTM
outputs, (hidden, cell) = self.lstm(packed)
# Unpack outputs
outputs, _ = nn.utils.rnn.pad_packed_sequence(outputs, batch_first=True)
# Combine bidirectional outputs
hidden = torch.cat([hidden[-2], hidden[-1]], dim=1) # [batch_size, 2*hidden_size]
hidden = torch.tanh(self.fc(hidden)) # [batch_size, hidden_size]
# Reshape for decoder
hidden = hidden.unsqueeze(0).repeat(self.num_layers, 1, 1) # [num_layers, batch_size, hidden_size]
return outputs, hidden
Implementation of a Transformer Encoder Layer
class TransformerEncoderLayer(nn.Module):
def __init__(self, d_model, nhead, dim_feedforward=2048, dropout=0.1):
"""
Arguments:
d_model: Model dimension/embedding size
nhead: Number of attention heads
dim_feedforward: Dimension of feed-forward network
dropout: Dropout probability
"""
super(TransformerEncoderLayer, self).__init__()
# Multi-head self-attention
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
# Feed-forward network
self.feed_forward = nn.Sequential(
nn.Linear(d_model, dim_feedforward),
nn.ReLU(),
nn.Dropout(dropout),
nn.Linear(dim_feedforward, d_model)
)
# Normalization layers
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
# Dropout
self.dropout1 = nn.Dropout(dropout)
self.dropout2 = nn.Dropout(dropout)
def forward(self, src, src_mask=None, src_key_padding_mask=None):
"""
Arguments:
src: Source sequence [seq_len, batch_size, d_model]
src_mask: Mask to prevent attention to certain positions
src_key_padding_mask: Mask for padded positions
Returns:
output: Encoded output [seq_len, batch_size, d_model]
"""
# Self-attention block
attn_output, _ = self.self_attn(
src, src, src,
attn_mask=src_mask,
key_padding_mask=src_key_padding_mask
)
src = src + self.dropout1(attn_output)
src = self.norm1(src)
# Feed-forward block
ff_output = self.feed_forward(src)
src = src + self.dropout2(ff_output)
src = self.norm2(src)
return src
<a name=”decoder”></a>
3. The Decoder: Deep Dive
Purpose and Function
The decoder generates the output sequence based on:
- The context representation from the encoder
- Previously generated outputs
- Its own internal state
Its main functions are:
- Interpreting the encoder’s representation
- Maintaining context during generation
- Producing coherent output sequences
Common Decoder Architectures
1. RNN-based Decoder
┌───────┐ ┌───────┐ ┌───────┐
│ RNN │───>│ RNN │───>│ RNN │ ...
└───────┘ └───────┘ └───────┘
↑ ↑ ↑ ↑ ↑ ↑
│ │ │ │ │ │
┌──┘ │ ┌──┘ │ ┌──┘ │
│ │ │ │ │ │
y₀ ctx y₁ ctx y₂ ctx
In an RNN decoder:
- Initialized with the encoder’s final state
- Takes previous output token and context as input
- Generates probability distribution for the next token
2. Attention-based Decoder
Attention Weights
↗ ↑ ↖
↗ │ ↖
┌───────┐↗ ┌───────┐ ↖┌───────┐
│ RNN │───>│ RNN │───>│ RNN │ ...
└───────┘ └───────┘ └───────┘
↑ ↑ ↑ ↑ ↑ ↑
│ │ │ │ │ │
┌──┘ │ ┌──┘ │ ┌──┘ │
│ │ │ │ │ │
y₀ ctx₀ y₁ ctx₁ y₂ ctx₂
With attention:
- Each decoder step has access to all encoder states
- Attention weights determine which encoder states to focus on
- Context vector is dynamically computed at each step
3. Transformer Decoder
Multi-Head Self-Attention
↑
|
Add & Normalize
↑
|
Multi-Head Cross-Attention
↑
|
Add & Normalize
↑
|
Feed-Forward Neural Network
↑
|
Add & Normalize
↑
|
Output Embedding
↑
|
Shifted Right Input
Transformer decoders:
- Use masked self-attention to prevent looking at future positions
- Include cross-attention to encoder outputs
- Process previously generated tokens in parallel during training
Implementation of a Basic RNN Decoder
class DecoderRNN(nn.Module):
def __init__(self, output_size, hidden_size, embedding_size, num_layers=1, dropout=0.1):
"""
Arguments:
output_size: Size of target vocabulary
hidden_size: Size of the hidden state
embedding_size: Size of the word embeddings
num_layers: Number of RNN layers
dropout: Dropout probability
"""
super(DecoderRNN, self).__init__()
self.hidden_size = hidden_size
self.output_size = output_size
self.num_layers = num_layers
# Word embedding layer
self.embedding = nn.Embedding(output_size, embedding_size)
# LSTM layer
self.lstm = nn.LSTM(
embedding_size,
hidden_size,
num_layers=num_layers,
dropout=dropout if num_layers > 1 else 0,
batch_first=True
)
# Output projection
self.fc_out = nn.Linear(hidden_size, output_size)
# Dropout
self.dropout = nn.Dropout(dropout)
def forward(self, input, hidden, cell):
"""
Arguments:
input: Input token indices [batch_size, 1]
hidden: Hidden state from encoder or previous step [num_layers, batch_size, hidden_size]
cell: Cell state [num_layers, batch_size, hidden_size]
Returns:
output: Next token probabilities [batch_size, output_size]
hidden: Updated hidden state
cell: Updated cell state
"""
# Embed input tokens
embedded = self.dropout(self.embedding(input)) # [batch_size, 1, embedding_size]
# Pass through LSTM
output, (hidden, cell) = self.lstm(embedded, (hidden, cell))
# output: [batch_size, 1, hidden_size]
# Project to vocabulary size
prediction = self.fc_out(output.squeeze(1)) # [batch_size, output_size]
return prediction, hidden, cell
Implementation of a Decoder with Attention
class AttentionDecoder(nn.Module):
def __init__(self, output_size, hidden_size, embedding_size, attention_size, num_layers=1, dropout=0.1):
"""
Arguments:
output_size: Size of target vocabulary
hidden_size: Size of the hidden state
embedding_size: Size of the word embeddings
attention_size: Size of attention layer
num_layers: Number of RNN layers
dropout: Dropout probability
"""
super(AttentionDecoder, self).__init__()
self.hidden_size = hidden_size
self.output_size = output_size
# Word embedding layer
self.embedding = nn.Embedding(output_size, embedding_size)
# Attention mechanism
self.attention = nn.Linear(hidden_size * 2, attention_size)
self.attention_combine = nn.Linear(hidden_size + embedding_size, hidden_size)
# LSTM layer
self.lstm = nn.LSTM(
hidden_size,
hidden_size,
num_layers=num_layers,
dropout=dropout if num_layers > 1 else 0,
batch_first=True
)
# Output projection
self.fc_out = nn.Linear(hidden_size, output_size)
# Dropout
self.dropout = nn.Dropout(dropout)
def forward(self, input, hidden, cell, encoder_outputs):
"""
Arguments:
input: Input token indices [batch_size, 1]
hidden: Hidden state [num_layers, batch_size, hidden_size]
cell: Cell state [num_layers, batch_size, hidden_size]
encoder_outputs: All encoder hidden states [batch_size, input_length, hidden_size]
"""
# Embed input tokens
embedded = self.dropout(self.embedding(input)) # [batch_size, 1, embedding_size]
# Calculate attention weights
h_top = hidden[-1].unsqueeze(1) # Get top layer's hidden state [batch_size, 1, hidden_size]
# Repeat for concatenation with encoder outputs
h_expanded = h_top.repeat(1, encoder_outputs.size(1), 1) # [batch_size, input_length, hidden_size]
# Concatenate
attn_input = torch.cat((encoder_outputs, h_expanded), dim=2) # [batch_size, input_length, hidden_size*2]
# Calculate attention scores
attn_scores = self.attention(attn_input) # [batch_size, input_length, attention_size]
attn_scores = torch.tanh(attn_scores)
attn_scores = torch.sum(attn_scores, dim=2) # [batch_size, input_length]
# Convert scores to weights with softmax
attn_weights = F.softmax(attn_scores, dim=1).unsqueeze(1) # [batch_size, 1, input_length]
# Apply attention weights to encoder outputs
context = torch.bmm(attn_weights, encoder_outputs) # [batch_size, 1, hidden_size]
# Combine context with input embedding
rnn_input = torch.cat((embedded, context), dim=2) # [batch_size, 1, embedding_size + hidden_size]
rnn_input = self.attention_combine(rnn_input) # [batch_size, 1, hidden_size]
rnn_input = F.relu(rnn_input)
# Pass through LSTM
output, (hidden, cell) = self.lstm(rnn_input, (hidden, cell))
# Project to vocabulary size
prediction = self.fc_out(output.squeeze(1)) # [batch_size, output_size]
return prediction, hidden, cell, attn_weights
Implementation of a Transformer Decoder Layer
class TransformerDecoderLayer(nn.Module):
def __init__(self, d_model, nhead, dim_feedforward=2048, dropout=0.1):
"""
Arguments:
d_model: Model dimension/embedding size
nhead: Number of attention heads
dim_feedforward: Dimension of feed-forward network
dropout: Dropout probability
"""
super(TransformerDecoderLayer, self).__init__()
# Multi-head self-attention
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
# Multi-head cross-attention to encoder outputs
self.multihead_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
# Feed-forward network
self.feed_forward = nn.Sequential(
nn.Linear(d_model, dim_feedforward),
nn.ReLU(),
nn.Dropout(dropout),
nn.Linear(dim_feedforward, d_model)
)
# Normalization layers
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.norm3 = nn.LayerNorm(d_model)
# Dropout
self.dropout1 = nn.Dropout(dropout)
self.dropout2 = nn.Dropout(dropout)
self.dropout3 = nn.Dropout(dropout)
def forward(self, tgt, memory, tgt_mask=None, memory_mask=None,
tgt_key_padding_mask=None, memory_key_padding_mask=None):
"""
Arguments:
tgt: Target sequence [tgt_len, batch_size, d_model]
memory: Memory from encoder [src_len, batch_size, d_model]
tgt_mask: Mask to prevent attention to future positions
memory_mask: Mask for encoder memory
tgt_key_padding_mask: Mask for padded positions in target
memory_key_padding_mask: Mask for padded positions in memory
Returns:
tgt: Decoded output [tgt_len, batch_size, d_model]
"""
# Self-attention block with mask to prevent attending to future positions
q = k = v = tgt
tgt2, _ = self.self_attn(
q, k, v,
attn_mask=tgt_mask,
key_padding_mask=tgt_key_padding_mask
)
tgt = tgt + self.dropout1(tgt2)
tgt = self.norm1(tgt)
# Cross-attention block between decoder queries and encoder keys/values
tgt2, _ = self.multihead_attn(
query=tgt,
key=memory,
value=memory,
attn_mask=memory_mask,
key_padding_mask=memory_key_padding_mask
)
tgt = tgt + self.dropout2(tgt2)
tgt = self.norm2(tgt)
# Feed-forward block
tgt2 = self.feed_forward(tgt)
tgt = tgt + self.dropout3(tgt2)
tgt = self.norm3(tgt)
return tgt
<a name=”attention”></a>
4. Attention Mechanisms
Why Attention?
The attention mechanism was developed to address a fundamental limitation of the basic encoder-decoder architecture:
- Problem: Fixed-size context vector becomes an information bottleneck, especially for long sequences
- Solution: Allow decoder to directly access all encoder hidden states, weighting them based on relevance
How Attention Works
- For each decoder step, calculate a set of attention scores between:
- Current decoder hidden state (query)
- Each encoder hidden state (keys)
- Convert scores to weights using softmax
- Weights sum to 1, acting as a probability distribution over encoder states
- Create context vector as weighted sum of encoder states
- Multiply each encoder state by its weight and sum
- Use context vector along with current decoder state to predict next output
Types of Attention
1. Bahdanau/Additive Attention
score(s_t, h_i) = v_a^T tanh(W_a[s_t; h_i])
- Concatenates decoder state and encoder state
- Passes through a feed-forward layer
- Projects to a scalar score
2. Luong/Multiplicative Attention
score(s_t, h_i) = s_t^T W_a h_i
- Uses dot product between transformed decoder and encoder states
- Computationally more efficient
3. Scaled Dot-Product Attention
Attention(Q, K, V) = softmax(QK^T / √d_k)V
- Used in Transformers
- Scales dot product to prevent small gradients with large dimensions
4. Multi-Head Attention
MultiHead(Q, K, V) = Concat(head_1, ..., head_h)W^O
where head_i = Attention(QW_i^Q, KW_i^K, VW_i^V)
- Projects queries, keys, and values h times
- Performs attention on each projection
- Concatenates results and projects again
Implementation of Basic Attention Mechanism
class Attention(nn.Module):
def __init__(self, hidden_size, method="dot"):
"""
Arguments:
hidden_size: Size of hidden states
method: Attention method ('dot', 'general', 'concat')
"""
super(Attention, self).__init__()
self.hidden_size = hidden_size
self.method = method
if method == 'general':
self.attn = nn.Linear(hidden_size, hidden_size)
elif method == 'concat':
self.attn = nn.Linear(hidden_size * 2, hidden_size)
self.v = nn.Parameter(torch.FloatTensor(1, hidden_size))
def forward(self, hidden, encoder_outputs):
"""
Arguments:
hidden: Current decoder hidden state [batch_size, hidden_size]
encoder_outputs: All encoder hidden states [batch_size, seq_len, hidden_size]
Returns:
attention_weights: Attention weights [batch_size, seq_len]
"""
batch_size = encoder_outputs.size(0)
seq_len = encoder_outputs.size(1)
# Create a score for each encoder output
if self.method == 'dot':
# Simple dot product between decoder hidden and encoder outputs
energy = torch.bmm(
hidden.unsqueeze(1), # [batch_size, 1, hidden_size]
encoder_outputs.transpose(1, 2) # [batch_size, hidden_size, seq_len]
) # [batch_size, 1, seq_len]
return F.softmax(energy.squeeze(1), dim=1)
elif self.method == 'general':
# Linear transformation then dot product
energy = torch.bmm(
hidden.unsqueeze(1), # [batch_size, 1, hidden_size]
self.attn(encoder_outputs).transpose(1, 2) # [batch_size, hidden_size, seq_len]
) # [batch_size, 1, seq_len]
return F.softmax(energy.squeeze(1), dim=1)
elif self.method == 'concat':
# Concatenation-based attention
hidden_expanded = hidden.unsqueeze(1).expand(-1, seq_len, -1) # [batch_size, seq_len, hidden_size]
concat = torch.cat((hidden_expanded, encoder_outputs), dim=2) # [batch_size, seq_len, 2*hidden_size]
energy = self.attn(concat) # [batch_size, seq_len, hidden_size]
energy = torch.tanh(energy)
energy = torch.bmm(
self.v.repeat(batch_size, 1, 1), # [batch_size, 1, hidden_size]
energy.transpose(1, 2) # [batch_size, hidden_size, seq_len]
) # [batch_size, 1, seq_len]
return F.softmax(energy.squeeze(1), dim=1)
Implementation of Scaled Dot-Product Attention
def scaled_dot_product_attention(query, key, value, mask=None):
"""
Compute scaled dot-product attention.
Arguments:
query: Query tensors [batch_size, num_heads, query_len, depth]
key: Key tensors [batch_size, num_heads, key_len, depth]
value: Value tensors [batch_size, num_heads, value_len, depth]
mask: Optional mask [batch_size, num_heads, query_len, key_len]
Returns:
output: Attention output [batch_size, num_heads, query_len, depth]
attention_weights: Attention weights [batch_size, num_heads, query_len, key_len]
"""
# Calculate dot product of query and key
matmul_qk = torch.matmul(query, key.transpose(-2, -1)) # [batch_size, num_heads, query_len, key_len]
# Scale by square root of the depth
depth = query.size(-1)
matmul_qk = matmul_qk / math.sqrt(depth)
# Apply mask if provided
if mask is not None:
matmul_qk = matmul_qk.masked_fill(mask == 0, -1e9)
# Apply softmax to get attention weights
attention_weights = F.softmax(matmul_qk, dim=-1) # [batch_size, num_heads, query_len, key_len]
# Apply attention weights to values
output = torch.matmul(attention_weights, value) # [batch_size, num_heads, query_len, depth]
return output, attention_weights
<a name=”implementation”></a>
5. Implementation: Neural Machine Translation
Now, let’s implement a complete encoder-decoder model for machine translation. We’ll build a sequence-to-sequence model with attention for translating between languages.
Complete Seq2Seq Model with Attention
import torch
import torch.nn as nn
import torch.nn.functional as F
import random
class Encoder(nn.Module):
def __init__(self, input_size, embedding_size, hidden_size, num_layers, dropout):
super(Encoder, self).__init__()
self.hidden_size = hidden_size
self.num_layers = num_layers
self.embedding = nn.Embedding(input_size, embedding_size)
self.dropout = nn.Dropout(dropout)
self.rnn = nn.GRU(
embedding_size,
hidden_size,
num_layers=num_layers,
bidirectional=True,
dropout=dropout if num_layers > 1 else 0,
batch_first=True
)
self.fc = nn.Linear(hidden_size * 2, hidden_size)
def forward(self, x, lengths):
# x: [batch_size, seq_len]
embedded = self.dropout(self.embedding(x)) # [batch_size, seq_len, embedding_size]
# Pack padded sequences
packed = nn.utils.rnn.pack_padded_sequence(
embedded, lengths.cpu(), batch_first=True, enforce_sorted=False
)
outputs, hidden = self.rnn(packed)
# Unpack outputs
outputs, _ = nn.utils.rnn.pad_packed_sequence(outputs, batch_first=True)
# outputs: [batch_size, seq_len, hidden_size*2]
# Combine bidirectional states
hidden = torch.cat([hidden[-2], hidden[-1]], dim=1) # [batch_size, hidden_size*2]
hidden = self.fc(hidden) # [batch_size, hidden_size]
hidden = torch.tanh(hidden)
# Reshape for decoder initialization
hidden = hidden.unsqueeze(0).repeat(self.num_layers, 1, 1) # [num_layers, batch_size, hidden_size]
return outputs, hidden
class Attention(nn.Module

Types of Recurrent Neural Networks: Architectures, Examples and Implementation
Recurrent Neural Networks (RNNs) are powerful sequence processing models that can handle data with temporal relationships. Unlike traditional feedforward neural networks, RNNs have connections that form directed cycles, allowing them to maintain memory of previous inputs. This makes them particularly effective for tasks involving sequential data like text, speech, time series, and more.
In this blog, we’ll explore different RNN architectures based on their input-output relationships, along with practical examples and implementations for each type.
Table of Contents
- One-to-One RNNs
- One-to-Many RNNs
- Many-to-One RNNs
- Many-to-Many RNNs (Synchronized)
- Many-to-Many RNNs (Encoder-Decoder)
- Advanced RNN Architectures
One-to-One RNNs
Architecture
One-to-One RNNs are the simplest form and technically not recurrent at all. They take a single input and produce a single output, much like a standard feedforward neural network.
Input(x) → Neural Network → Output(y)
Example Use Case
Image classification, where a single image is classified into a single category.
Implementation
import torch
import torch.nn as nn
class SimpleNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleNN, self).__init__()
self.layer1 = nn.Linear(input_size, hidden_size)
self.relu = nn.ReLU()
self.layer2 = nn.Linear(hidden_size, output_size)
def forward(self, x):
out = self.layer1(x)
out = self.relu(out)
out = self.layer2(out)
return out
# Example usage
input_size = 784 # For MNIST
hidden_size = 128
output_size = 10 # 10 digits
model = SimpleNN(input_size, hidden_size, output_size)
# For a single input
x = torch.randn(1, input_size)
output = model(x)
print(output.shape) # torch.Size([1, 10])
Explanation
This isn’t truly an RNN since it lacks recurrence, but it’s included as a baseline for comparison. The model takes a flattened image (784 pixels for MNIST) and outputs probabilities for 10 digit classes.
One-to-Many RNNs
Architecture
One-to-Many RNNs take a single input and produce a sequence of outputs. The input is processed once, and then the network generates a series of outputs recursively.
Single Input(x) → RNN → Output sequence(y₁, y₂, ..., yₙ)
Example Use Case
Image captioning, where a single image generates a sequence of words describing it.
Implementation
import torch
import torch.nn as nn
class ImageCaptioningRNN(nn.Module):
def __init__(self, image_feature_size, hidden_size, vocab_size, seq_length):
super(ImageCaptioningRNN, self).__init__()
self.hidden_size = hidden_size
self.seq_length = seq_length
# Image feature to hidden state
self.image_to_hidden = nn.Linear(image_feature_size, hidden_size)
# RNN cell (using GRU for simplicity)
self.rnn_cell = nn.GRUCell(hidden_size, hidden_size)
# Output layer
self.hidden_to_output = nn.Linear(hidden_size, vocab_size)
def forward(self, image_features):
batch_size = image_features.size(0)
# Initialize hidden state from image features
hidden = self.image_to_hidden(image_features)
# Container for outputs
outputs = []
# Input for first step is the hidden state
input_t = hidden
# Generate sequence
for t in range(self.seq_length):
# Update hidden state
hidden = self.rnn_cell(input_t, hidden)
# Generate output for this timestep
output = self.hidden_to_output(hidden)
outputs.append(output)
# Next input is the current hidden state
input_t = hidden
# Stack outputs along sequence dimension
outputs = torch.stack(outputs, dim=1)
return outputs
# Example usage
image_feature_size = 2048 # From a CNN like ResNet
hidden_size = 512
vocab_size = 10000
seq_length = 20 # Maximum caption length
model = ImageCaptioningRNN(image_feature_size, hidden_size, vocab_size, seq_length)
# For a batch of images
image_features = torch.randn(32, image_feature_size)
captions = model(image_features)
print(captions.shape) # torch.Size([32, 20, 10000])
Explanation
This RNN uses a single image input to generate a sequence of words. After processing the image features to create an initial hidden state, the model recursively generates each word based on the previous hidden state. At each step, the output is a probability distribution over the vocabulary.
Many-to-One RNNs
Architecture
Many-to-One RNNs process a sequence of inputs and produce a single output, typically at the end of the sequence.
Input sequence(x₁, x₂, ..., xₙ) → RNN → Single Output(y)
Example Use Case
Sentiment analysis of text, where a sequence of words is classified as positive or negative.
Implementation
import torch
import torch.nn as nn
class SentimentRNN(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_size, output_size):
super(SentimentRNN, self).__init__()
self.hidden_size = hidden_size
# Word embeddings
self.embedding = nn.Embedding(vocab_size, embedding_dim)
# RNN layer
self.rnn = nn.GRU(embedding_dim, hidden_size, batch_first=True)
# Output layer
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, x):
# x shape: (batch_size, sequence_length)
# Embed the input sequence
x = self.embedding(x) # (batch_size, sequence_length, embedding_dim)
# Process through RNN
_, hidden = self.rnn(x) # hidden: (1, batch_size, hidden_size)
# Use the final hidden state
hidden = hidden.squeeze(0) # (batch_size, hidden_size)
# Pass through output layer
output = self.fc(hidden) # (batch_size, output_size)
return output
# Example usage
vocab_size = 20000
embedding_dim = 300
hidden_size = 256
output_size = 2 # Binary sentiment (positive/negative)
model = SentimentRNN(vocab_size, embedding_dim, hidden_size, output_size)
# For a batch of sequences
batch_size = 64
sequence_length = 100
input_sequences = torch.randint(0, vocab_size, (batch_size, sequence_length))
sentiment = model(input_sequences)
print(sentiment.shape) # torch.Size([64, 2])
Explanation
This model processes a sequence of word indices, embeds them, and passes them through a GRU layer. Only the final hidden state is used to make the prediction, which is then passed through a linear layer to get the sentiment classification.
Many-to-Many RNNs (Synchronized)
Architecture
In synchronized Many-to-Many RNNs, there’s an output for each input at the same time step.
Input sequence(x₁, x₂, ..., xₙ) → RNN → Output sequence(y₁, y₂, ..., yₙ)
Example Use Case
Part-of-speech tagging, where each word in a sentence is tagged with its grammatical role.
Implementation
import torch
import torch.nn as nn
class POSTaggerRNN(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_size, num_tags):
super(POSTaggerRNN, self).__init__()
# Word embeddings
self.embedding = nn.Embedding(vocab_size, embedding_dim)
# Bidirectional RNN for better context
self.rnn = nn.LSTM(embedding_dim, hidden_size, batch_first=True, bidirectional=True)
# Output layer (accounting for bidirectionality)
self.fc = nn.Linear(hidden_size * 2, num_tags)
def forward(self, x):
# x shape: (batch_size, sequence_length)
# Embed the input sequence
x = self.embedding(x) # (batch_size, sequence_length, embedding_dim)
# Process through RNN
outputs, _ = self.rnn(x) # outputs: (batch_size, sequence_length, hidden_size*2)
# Pass each output through the final layer
tag_space = self.fc(outputs) # (batch_size, sequence_length, num_tags)
return tag_space
# Example usage
vocab_size = 20000
embedding_dim = 300
hidden_size = 256
num_tags = 45 # Number of POS tags
model = POSTaggerRNN(vocab_size, embedding_dim, hidden_size, num_tags)
# For a batch of sequences
batch_size = 32
sequence_length = 50
input_sequences = torch.randint(0, vocab_size, (batch_size, sequence_length))
pos_tags = model(input_sequences)
print(pos_tags.shape) # torch.Size([32, 50, 45])
Explanation
This bidirectional LSTM processes a sequence of words and outputs a tag prediction for each word in the sequence. The model embeds each word, processes the entire sequence with a bidirectional LSTM to capture context in both directions, and then maps each hidden state to a tag probability distribution.
Many-to-Many RNNs (Encoder-Decoder)
Architecture
The encoder-decoder architecture first processes the entire input sequence (encoder) and then generates an output sequence (decoder), possibly of different length.
Input sequence(x₁, x₂, ..., xₙ) → Encoder → [State] → Decoder → Output sequence(y₁, y₂, ..., yₘ)
Example Use Case
Machine translation, where a sentence in one language is translated to another language.
Implementation
import torch
import torch.nn as nn
import torch.nn.functional as F
class Encoder(nn.Module):
def __init__(self, input_vocab_size, embedding_dim, hidden_size):
super(Encoder, self).__init__()
self.hidden_size = hidden_size
self.embedding = nn.Embedding(input_vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_size, batch_first=True)
def forward(self, x):
# x shape: (batch_size, sequence_length)
embedded = self.embedding(x) # (batch_size, sequence_length, embedding_dim)
outputs, (hidden, cell) = self.lstm(embedded)
return outputs, hidden, cell
class Decoder(nn.Module):
def __init__(self, output_vocab_size, embedding_dim, hidden_size):
super(Decoder, self).__init__()
self.hidden_size = hidden_size
self.embedding = nn.Embedding(output_vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_size, batch_first=True)
self.fc = nn.Linear(hidden_size, output_vocab_size)
def forward(self, x, hidden, cell):
# x shape: (batch_size, 1)
embedded = self.embedding(x) # (batch_size, 1, embedding_dim)
output, (hidden, cell) = self.lstm(embedded, (hidden, cell))
# output: (batch_size, 1, hidden_size)
prediction = self.fc(output.squeeze(1)) # (batch_size, output_vocab_size)
return prediction, hidden, cell
class Seq2Seq(nn.Module):
def __init__(self, encoder, decoder, device):
super(Seq2Seq, self).__init__()
self.encoder = encoder
self.decoder = decoder
self.device = device
def forward(self, source, target, teacher_forcing_ratio=0.5):
# source: (batch_size, source_length)
# target: (batch_size, target_length)
batch_size = source.shape[0]
target_length = target.shape[1]
target_vocab_size = self.decoder.fc.out_features
# Tensor to store decoder outputs
outputs = torch.zeros(batch_size, target_length, target_vocab_size).to(self.device)
# Encode the source sequence
_, hidden, cell = self.encoder(source)
# First decoder input is the <SOS> token
decoder_input = target[:, 0].unsqueeze(1) # (batch_size, 1)
for t in range(1, target_length):
# Pass through decoder
output, hidden, cell = self.decoder(decoder_input, hidden, cell)
# Store prediction
outputs[:, t, :] = output
# Decide whether to use teacher forcing
teacher_force = torch.rand(1).item() < teacher_forcing_ratio
# Get the highest predicted token
top1 = output.argmax(1)
# Use either prediction or actual target as next input
decoder_input = target[:, t].unsqueeze(1) if teacher_force else top1.unsqueeze(1)
return outputs
# Example usage
input_vocab_size = 10000
output_vocab_size = 8000
embedding_dim = 256
hidden_size = 512
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
encoder = Encoder(input_vocab_size, embedding_dim, hidden_size).to(device)
decoder = Decoder(output_vocab_size, embedding_dim, hidden_size).to(device)
model = Seq2Seq(encoder, decoder, device).to(device)
# For a batch of sequences
batch_size = 16
source_length = 20
target_length = 25
source = torch.randint(0, input_vocab_size, (batch_size, source_length)).to(device)
target = torch.randint(0, output_vocab_size, (batch_size, target_length)).to(device)
output = model(source, target)
print(output.shape) # torch.Size([16, 25, 8000])
Explanation
This is a more complex sequence-to-sequence model with an encoder-decoder architecture. The encoder processes the entire input sequence and passes its final state to the decoder, which then generates an output sequence. The implementation includes teacher forcing, where during training the model sometimes uses the true target from the previous time step instead of its own prediction.
Advanced RNN Architectures
While the basic types above cover the fundamental input-output relationships, modern RNN applications often use more advanced architectures:
LSTM (Long Short-Term Memory)
LSTMs address the vanishing gradient problem in standard RNNs with a more complex cell structure that includes input, forget, and output gates.
GRU (Gated Recurrent Unit)
GRUs are a simplified version of LSTMs with fewer parameters but similar capabilities for long-term dependency modeling.
Bidirectional RNNs
These process sequences in both forward and backward directions to capture context from both past and future time steps.
Attention Mechanisms
Attention allows models to focus on relevant parts of the input sequence when generating each output element, significantly improving performance for tasks like translation.
Transformers
While not traditional RNNs, transformers have largely replaced RNNs in many sequence processing tasks due to their parallelization capabilities and stronger performance.
Conclusion
Recurrent Neural Networks offer versatile architectures for processing sequential data across various applications. From the simple one-to-many models for image captioning to the complex encoder-decoder structures for machine translation, RNNs and their variants enable powerful modeling of temporal dependencies.
Understanding the different input-output relationships in RNN architectures is crucial for selecting the right approach for your specific sequence processing task. While traditional RNNs have been widely used, more advanced architectures like LSTMs, GRUs, and attention-based models have pushed the boundaries of sequence modeling even further.
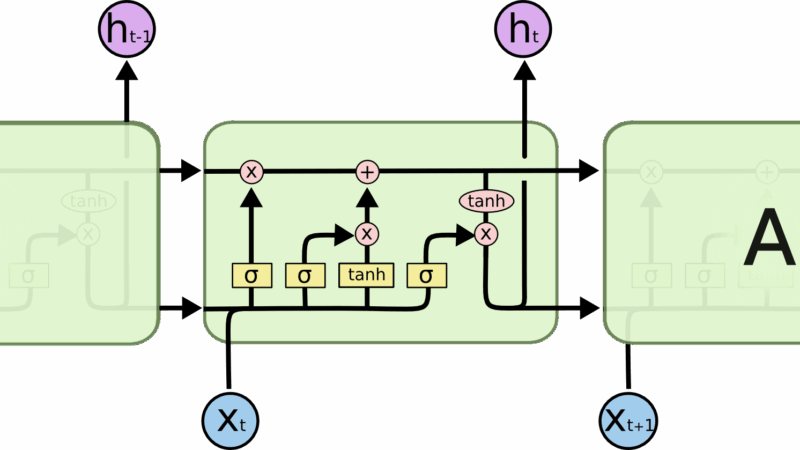
Understanding LSTM Networks with Forward and Backward Propagation Mathematical Intuitions
Recurrent Neural Networks
Humans don’t begin their thought process from zero every moment. As you read this essay, you interpret each word in the context of the ones that came before it. You don’t discard everything and restart your thinking each time — your thoughts carry forward.
Conventional neural networks lack this ability, which is a significant limitation. For instance, if you’re trying to identify what type of event is occurring at each moment in a movie, a traditional neural network struggles to incorporate knowledge of earlier scenes to make sense of later ones.
Recurrent neural networks (RNNs) overcome this limitation. These networks are designed with loops that allow information to be retained over time, enabling them to maintain context.

Recurrent Neural Networks have loops.
In the above diagram, a chunk of neural network, AA, looks at some input XtXt and outputs a value htht. A loop allows information to be passed from one step of the network to the next.
These loops make recurrent neural networks seem kind of mysterious. However, if you think a bit more, it turns out that they aren’t all that different than a normal neural network. A recurrent neural network can be thought of as multiple copies of the same network, each passing a message to a successor. Consider what happens if we unroll the loop:
An unrolled recurrent neural network.
The chain-like structure of recurrent neural networks (RNNs) makes them naturally suited for handling sequential data, such as lists and time series. They’re the go-to neural network architecture for this kind of information.
And indeed, they’ve been widely adopted! In recent years, RNNs have driven remarkable progress in fields like speech recognition, language modeling, translation, image captioning, and more.
A major factor behind these achievements is the use of LSTMs — a specialized type of RNN that outperforms the standard model on many tasks. Most of the exciting advancements involving RNNs have been made possible thanks to LSTMs, and this essay will focus on exploring how they work.
The Problem of Long-Term Dependencies
One of the appeals of RNNs is the idea that they might be able to connect previous information to the present task, such as using previous video frames might inform the understanding of the present frame. If RNNs could do this, they’d be extremely useful. But can they? It depends.
Sometimes, we only need to look at recent information to perform the present task. For example, consider a language model trying to predict the next word based on the previous ones. If we are trying to predict the last word in “the clouds are in the sky,” we don’t need any further context – it’s pretty obvious the next word is going to be sky. In such cases, where the gap between the relevant information and the place that it’s needed is small, RNNs can learn to use the past information.
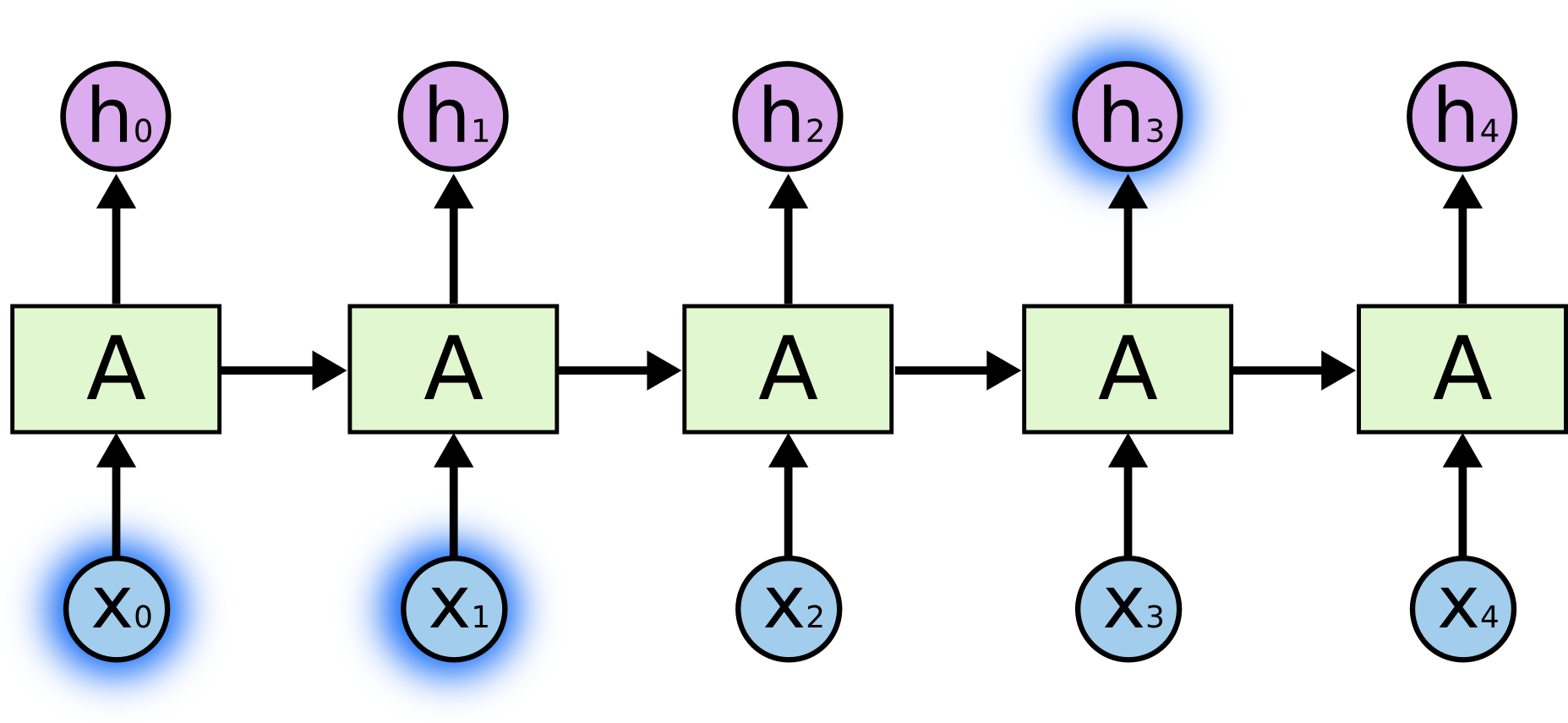
But there are also cases where we need more context. Consider trying to predict the last word in the text “I grew up in France… I speak fluent French.” Recent information suggests that the next word is probably the name of a language, but if we want to narrow down which language, we need the context of France, from further back. It’s entirely possible for the gap between the relevant information and the point where it is needed to become very large.
Unfortunately, as that gap grows, RNNs become unable to learn to connect the information.
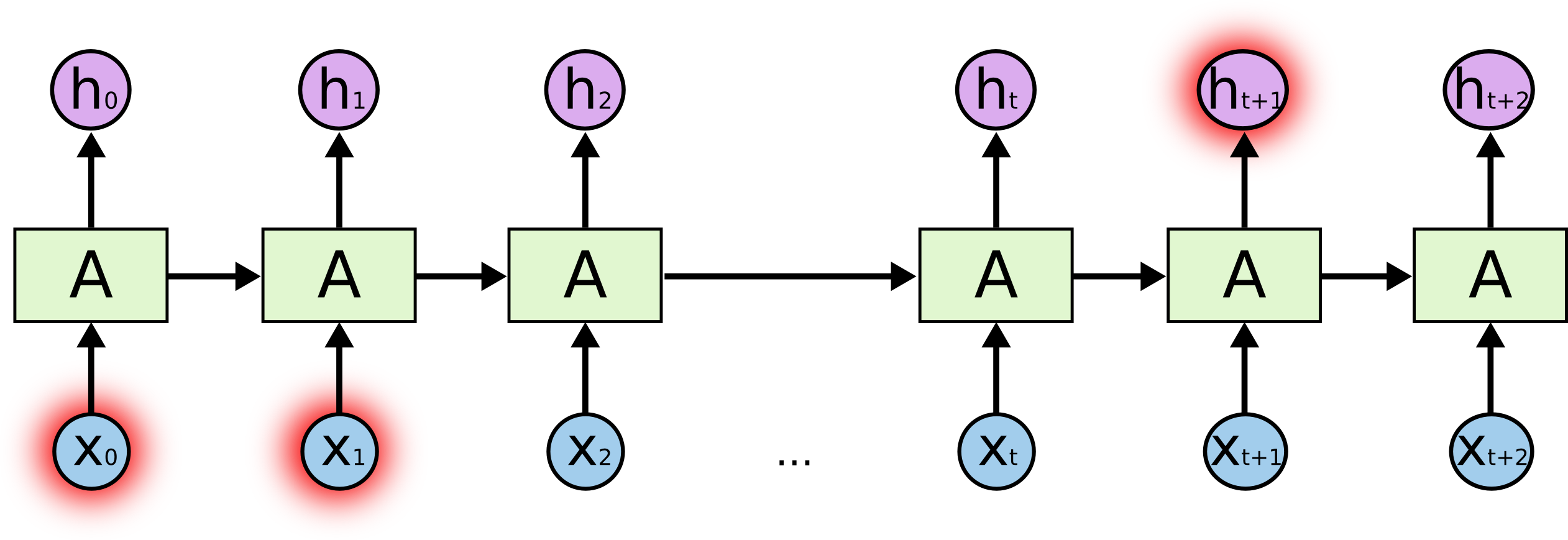
In theory, RNNs are absolutely capable of handling such “long-term dependencies.” A human could carefully pick parameters for them to solve toy problems of this form. Sadly, in practice, RNNs don’t seem to be able to learn them. The problem was explored in depth by Hochreiter (1991) [German] and Bengio, et al. (1994), who found some pretty fundamental reasons why it might be difficult.
Thankfully, LSTMs don’t have this problem!
LSTM Networks
Long Short-Term Memory networks, or simply LSTMs, are a specialized type of recurrent neural network (RNN) designed to learn and retain information over long sequences. First introduced by Hochreiter and Schmidhuber in 1997, they’ve since been improved and widely adopted due to their impressive performance across a broad range of tasks.
LSTMs are specifically built to overcome the challenge of long-term dependencies in sequence modeling. While standard RNNs often struggle to retain information across many time steps, LSTMs are inherently capable of doing so — maintaining relevant information over long periods is a core part of how they function.
Like all RNNs, LSTMs consist of a chain of repeating neural network modules. However, while a basic RNN typically uses a simple structure like a single tanh layer in each module, LSTMs replace this with a more sophisticated internal architecture designed to preserve and control information flow more effectively.
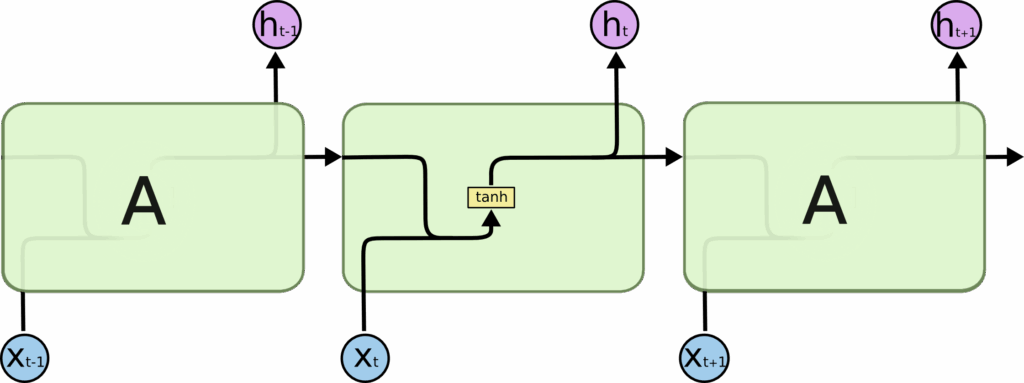
The Word1 Xt-1 sent to the neural network, then word2 is sent to the neural network , Xt-1 is provided as input to calculate ht, we calculate Cosine Similarity Between the Words to check the relation between them, with respect to the features.
The repeating module in a standard RNN contains a single layer.
LSTMs also have this chain like structure, but the repeating module has a different structure. Instead of having a single neural network layer, there are four, interacting in a very special way.
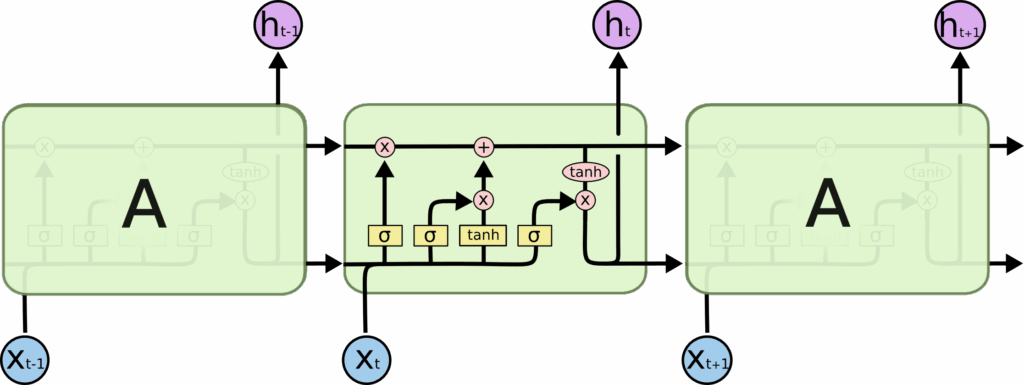
The repeating module in an LSTM contains four interacting layers.
Don’t worry about the details of what’s going on. We’ll walk through the LSTM diagram step by step later. For now, let’s just try to get comfortable with the notation we’ll be using.

In the above diagram, each line carries an entire vector, from the output of one node to the inputs of others. The pink circles represent pointwise operations, like vector addition, while the yellow boxes are learned neural network layers. Lines merging denote concatenation, while a line forking denote its content being copied and the copies going to different locations.
The Core Idea Behind LSTMs
The key to LSTMs is the cell state, the horizontal line running through the top of the diagram.
The cell state is kind of like a conveyor belt. It runs straight down the entire chain, with only some minor linear interactions. It’s very easy for information to just flow along it unchanged.
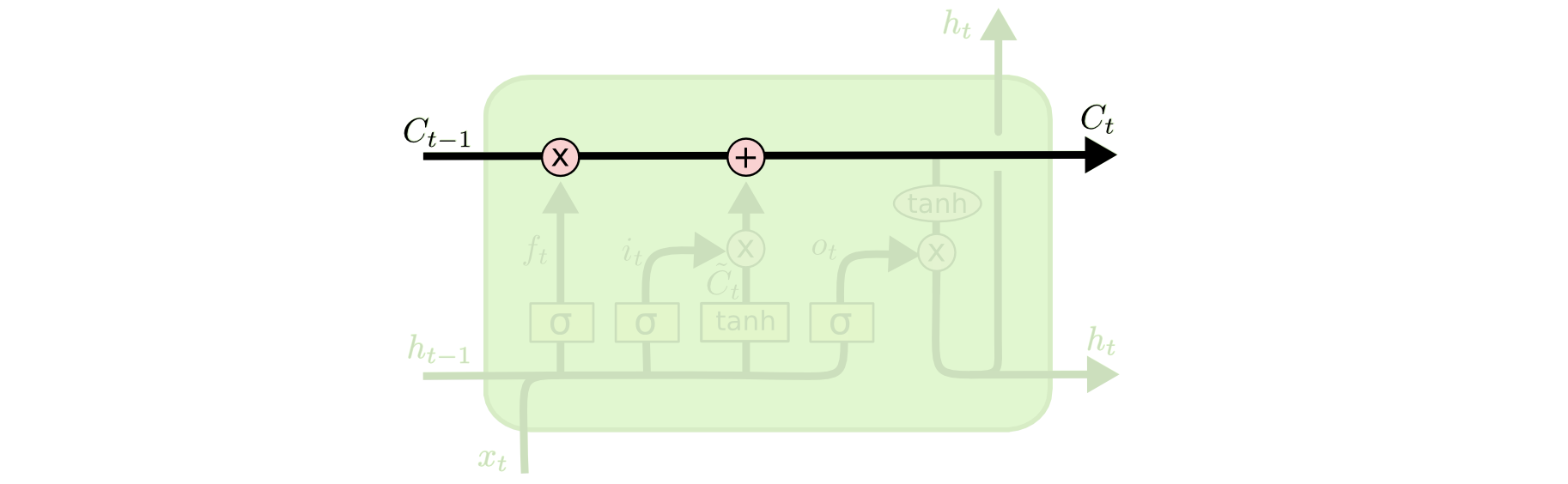
The LSTM does have the ability to remove or add information to the cell state, carefully regulated by structures called gates.
Gates are a way to optionally let information through. They are composed out of a sigmoid neural net layer and a pointwise multiplication operation.
The sigmoid layer outputs numbers between zero and one, describing how much of each component should be let through. A value of zero means “let nothing through,” while a value of one means “let everything through!”
An LSTM has three of these gates, to protect and control the cell state.
Step-by-Step LSTM Walk Through
The first step in our LSTM is to decide what information we’re going to throw away from the cell state. This decision is made by a sigmoid layer called the “forget gate layer.” It looks at ht−1ht−1 and xtxt, and outputs a number between 00 and 11 for each number in the cell state Ct−1Ct−1. A 11 represents “completely keep this” while a 00 represents “completely get rid of this.”
Let’s go back to our example of a language model trying to predict the next word based on all the previous ones. In such a problem, the cell state might include the gender of the present subject, so that the correct pronouns can be used. When we see a new subject, we want to forget the gender of the old subject.
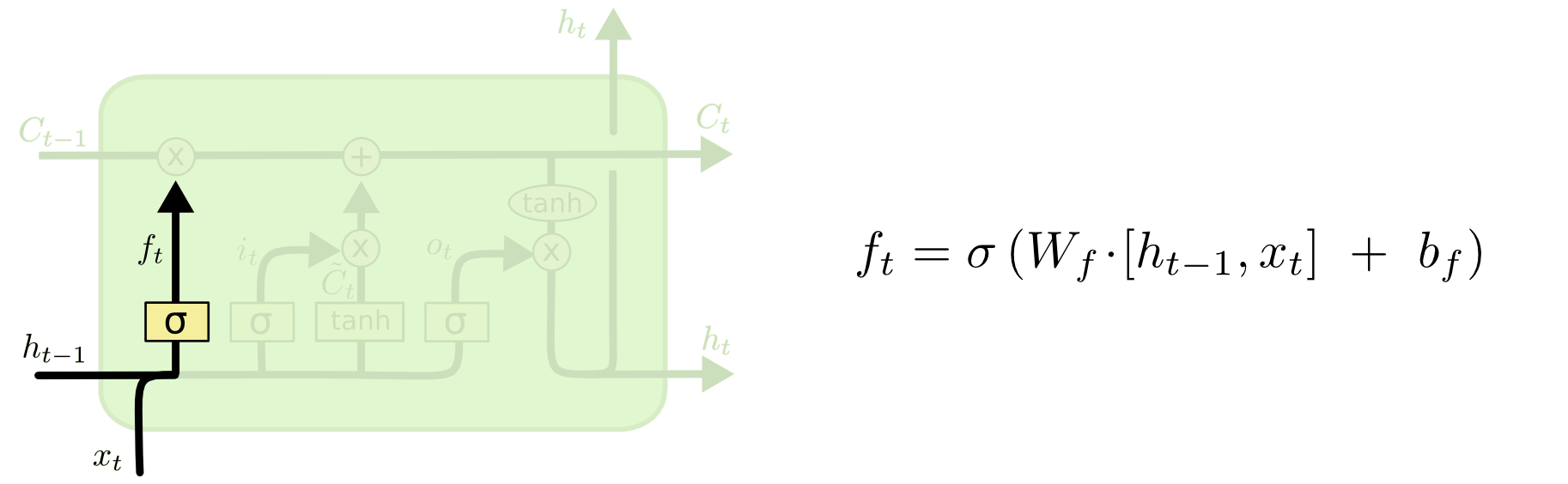
The next step is to decide what new information we’re going to store in the cell state. This has two parts. First, a sigmoid layer called the “input gate layer” decides which values we’ll update. Next, a tanh layer creates a vector of new candidate values, C~tC~t, that could be added to the state. In the next step, we’ll combine these two to create an update to the state.
In the example of our language model, we’d want to add the gender of the new subject to the cell state, to replace the old one we’re forgetting.
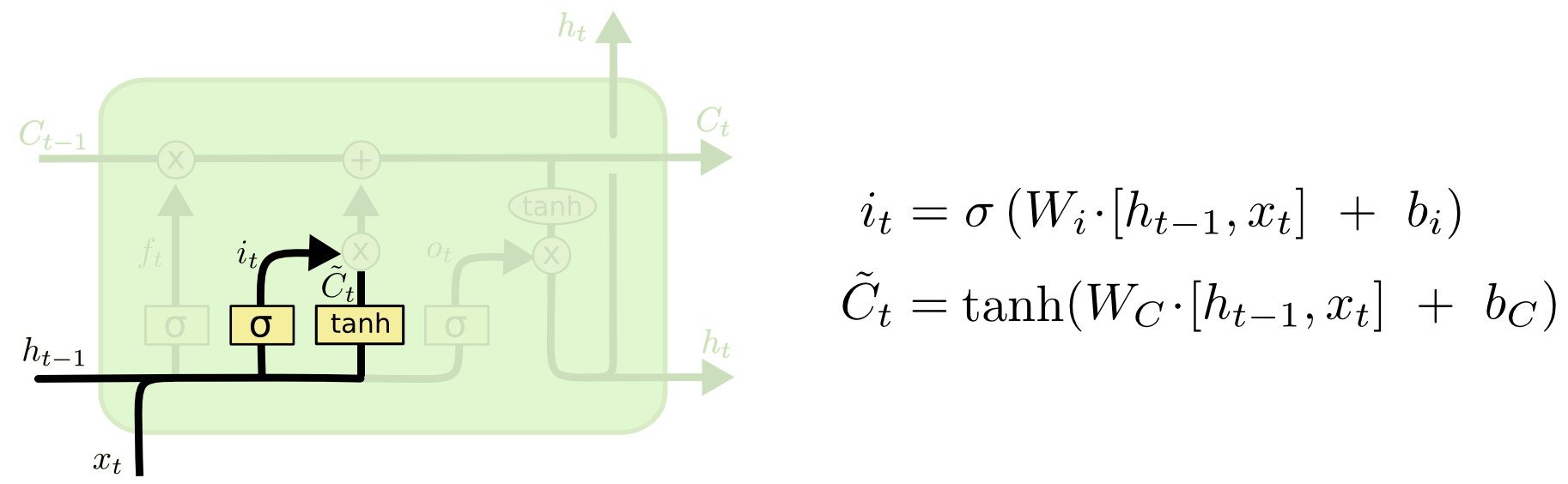
It’s now time to update the old cell state, Ct−1Ct−1, into the new cell state CtCt. The previous steps already decided what to do, we just need to actually do it.
We multiply the old state by ftft, forgetting the things we decided to forget earlier. Then we add it∗C~tit∗C~t. This is the new candidate values, scaled by how much we decided to update each state value.
In the case of the language model, this is where we’d actually drop the information about the old subject’s gender and add the new information, as we decided in the previous steps.
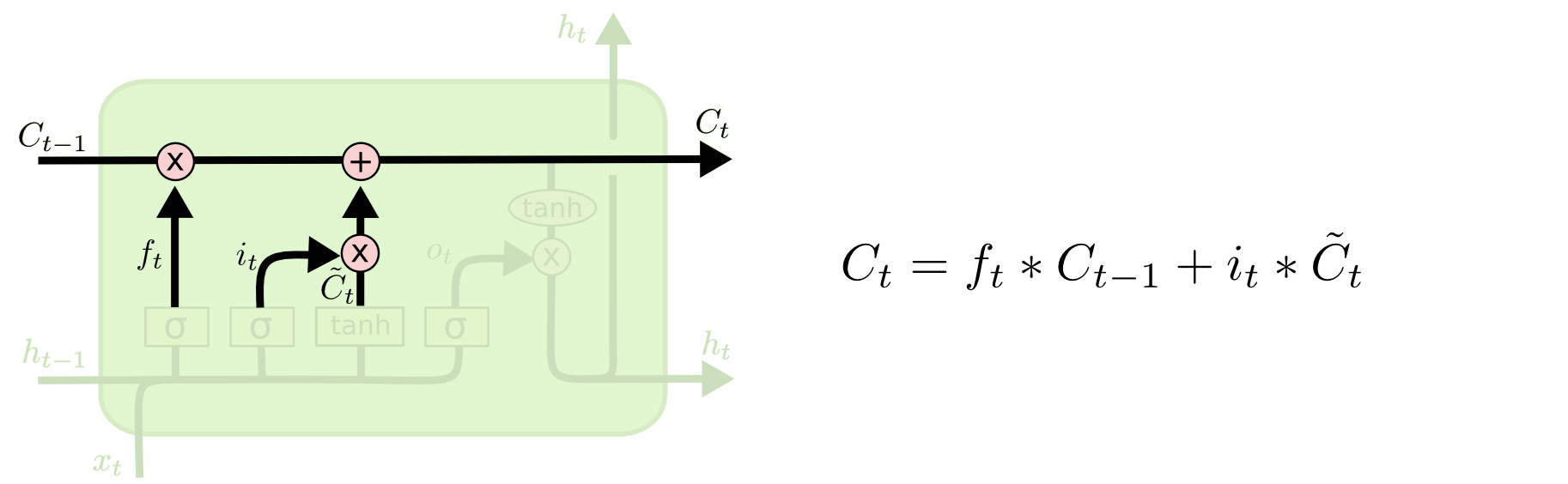
Finally, we need to decide what we’re going to output. This output will be based on our cell state, but will be a filtered version. First, we run a sigmoid layer which decides what parts of the cell state we’re going to output. Then, we put the cell state through tanhtanh (to push the values to be between −1−1 and 11) and multiply it by the output of the sigmoid gate, so that we only output the parts we decided to.
For the language model example, since it just saw a subject, it might want to output information relevant to a verb, in case that’s what is coming next. For example, it might output whether the subject is singular or plural, so that we know what form a verb should be conjugated into if that’s what follows next.
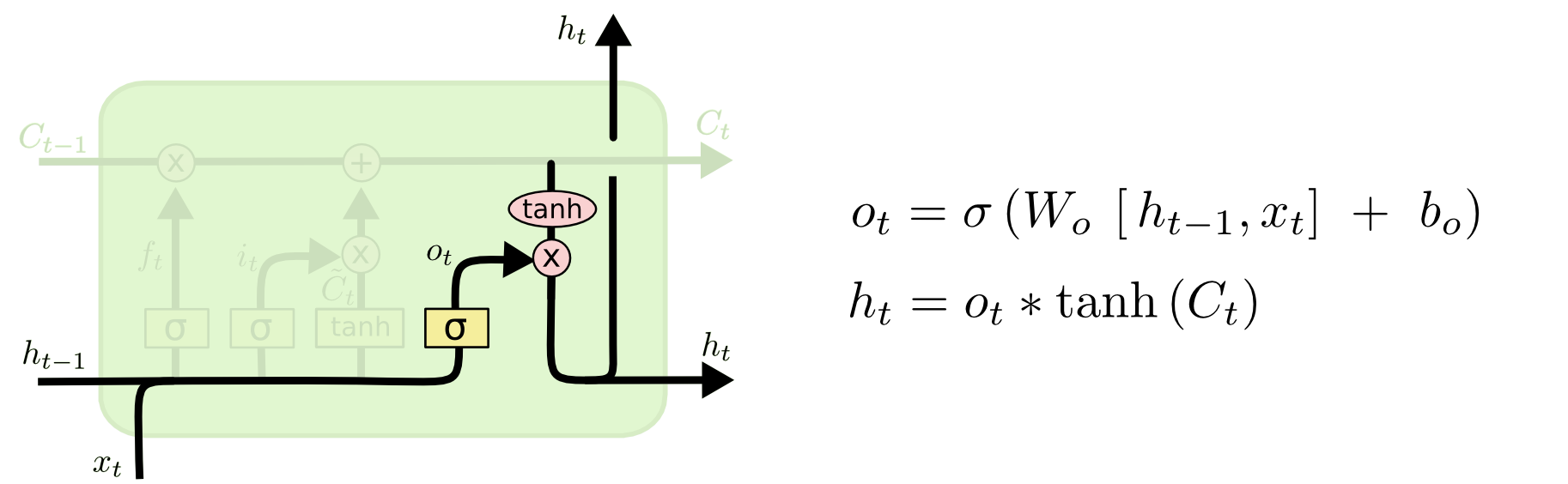
Variants on Long Short Term Memory
What I’ve described so far is a pretty normal LSTM. But not all LSTMs are the same as the above. In fact, it seems like almost every paper involving LSTMs uses a slightly different version. The differences are minor, but it’s worth mentioning some of them.
One popular LSTM variant, introduced by Gers & Schmidhuber (2000), is adding “peephole connections.” This means that we let the gate layers look at the cell state.
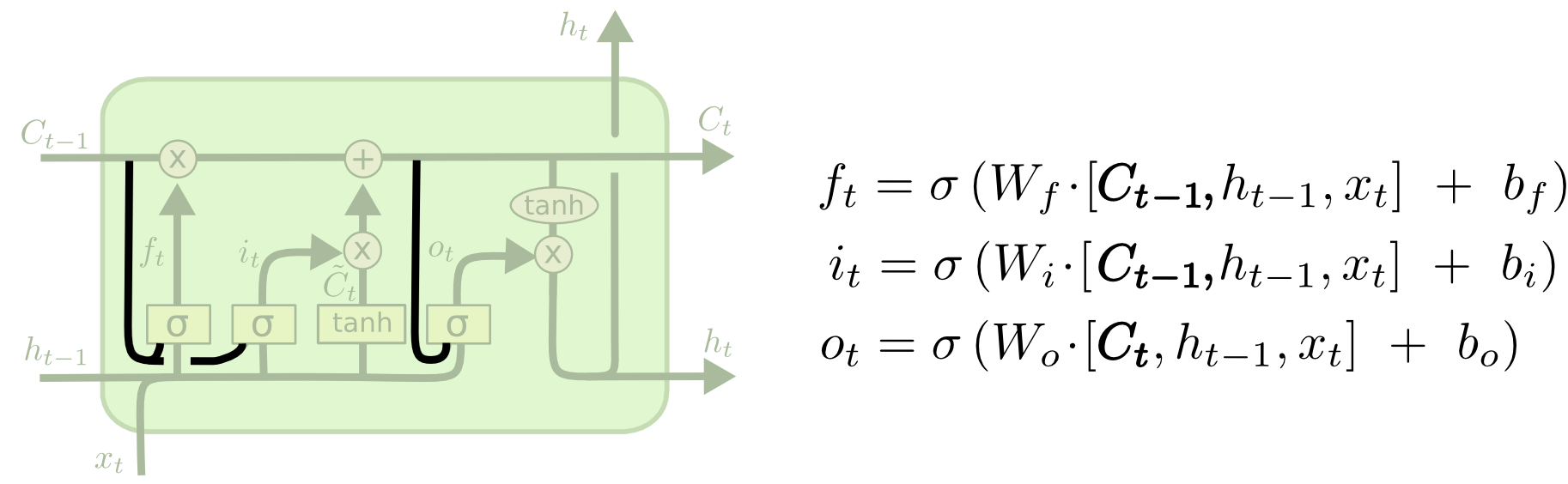
The above diagram adds peepholes to all the gates, but many papers will give some peepholes and not others.
Another variation is to use coupled forget and input gates. Instead of separately deciding what to forget and what we should add new information to, we make those decisions together. We only forget when we’re going to input something in its place. We only input new values to the state when we forget something older.
A slightly more dramatic variation on the LSTM is the Gated Recurrent Unit, or GRU, introduced by Cho, et al. (2014). It combines the forget and input gates into a single “update gate.” It also merges the cell state and hidden state, and makes some other changes. The resulting model is simpler than standard LSTM models, and has been growing increasingly popular.

These are only a few of the most notable LSTM variants. There are lots of others, like Depth Gated RNNs by Yao, et al. (2015). There’s also some completely different approach to tackling long-term dependencies, like Clockwork RNNs by Koutnik, et al. (2014).
Which of these variants is best? Do the differences matter? Greff, et al. (2015) do a nice comparison of popular variants, finding that they’re all about the same. Jozefowicz, et al. (2015) tested more than ten thousand RNN architectures, finding some that worked better than LSTMs on certain tasks.
Understanding RNN and LSTM: Forward and Backpropagation
Recurrent Neural Networks (RNNs) and Long Short-Term Memory networks (LSTMs) are fundamental architectures for sequence modeling in deep learning. This article provides a comprehensive mathematical foundation for both, including forward pass computations and the crucial backpropagation through time (BPTT) formulas for training.
1. Vanilla Recurrent Neural Networks (RNNs)
1.1 Forward Propagation
The standard RNN computes a sequence of hidden states and outputs from an input sequence:
For time step \(t\):
\begin{align} h_t &= \tanh(W_{hh} h_{t-1} + W_{xh} x_t + b_h) \\ y_t &= W_{hy} h_t + b_y \end{align}Where:
- \(x_t\) is the input at time step \(t\)
- \(h_t\) is the hidden state at time step \(t\)
- \(y_t\) is the output at time step \(t\)
- \(W_{xh}\) is the weight matrix from input to hidden layer
- \(W_{hh}\) is the recurrent weight matrix from hidden to hidden layer
- \(W_{hy}\) is the weight matrix from hidden to output layer
- \(b_h\) and \(b_y\) are bias vectors
- \(\tanh\) is the hyperbolic tangent activation function
1.2 Backpropagation Through Time (BPTT)
For a loss function \(L\) (typically cross-entropy for classification or mean squared error for regression), the gradients are:
Where \(\text{diag}(1 – h_{t+1}^2)\) represents the derivative of \(\tanh\) evaluated at the pre-activation values.
Note on the Vanishing/Exploding Gradient Problem: The recursion in calculating \(\frac{\partial L}{\partial h_t}\) involves multiplying by \(W_{hh}^T\) repeatedly, which can cause gradients to either vanish or explode during backpropagation through many time steps. This is a fundamental limitation of vanilla RNNs that LSTMs were designed to address.
2. Long Short-Term Memory Networks (LSTMs)
2.1 Forward Propagation
LSTMs introduce gating mechanisms to control information flow:
For time step \(t\):
\begin{align} f_t &= \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) \\ i_t &= \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) \\ \tilde{C}_t &= \tanh(W_C \cdot [h_{t-1}, x_t] + b_C) \\ C_t &= f_t \odot C_{t-1} + i_t \odot \tilde{C}_t \\ o_t &= \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) \\ h_t &= o_t \odot \tanh(C_t) \\ y_t &= W_{hy} h_t + b_y \end{align}Where:
- \(f_t\) is the forget gate, determining what to discard from the cell state
- \(i_t\) is the input gate, determining what new information to store
- \(\tilde{C}_t\) is the candidate cell state
- \(C_t\) is the cell state
- \(o_t\) is the output gate
- \(h_t\) is the hidden state
- \(y_t\) is the output
- \([h_{t-1}, x_t]\) represents the concatenation of \(h_{t-1}\) and \(x_t\)
- \(\odot\) represents element-wise multiplication
- \(\sigma\) is the sigmoid activation function
2.2 Backpropagation Through Time for LSTMs
LSTM backpropagation is more complex due to the multiple gates and pathways. Here are the key derivatives:
For the hidden state backpropagation:
For the cell state candidate and gates:
Then, for the weight matrices:
And for the bias terms:
3. Practical Implementation Considerations
3.1 Gradient Clipping
To mitigate exploding gradients, a common practice is to clip gradients when their norm exceeds a threshold:
\begin{align} \text{if } \|\nabla L\| > \text{threshold}: \nabla L \leftarrow \frac{\text{threshold}}{\|\nabla L\|} \nabla L \end{align}3.2 Initialization
Proper weight initialization is crucial for training RNNs and LSTMs:
- For vanilla RNNs, orthogonal initialization of \(W_{hh}\) helps with gradient flow
- For LSTMs, initializing forget gate biases \(b_f\) to positive values (often 1.0) encourages remembering by default
- Xavier/Glorot initialization for non-recurrent weights helps maintain variance across layers
4. Comparison Between RNN and LSTM
| Aspect | Vanilla RNN | LSTM |
|---|---|---|
| Memory capacity | Limited, prone to forgetting over long sequences | Enhanced with explicit cell state pathway |
| Gradient flow | Susceptible to vanishing/exploding gradients | Much better gradient flow through cell state |
| Parameter count | Lower | Higher (approximately 4x more parameters) |
| Computational complexity | Lower | Higher |
| Long-term dependencies | Struggles to capture | Effectively captures |
Understanding the forward and backward propagation mechanisms of RNNs and LSTMs provides crucial insights into their operational differences and relative strengths. While vanilla RNNs offer a simpler architecture with fewer parameters, LSTMs excel at capturing long-term dependencies through their sophisticated gating mechanisms, making them the preferred choice for many sequence modeling tasks despite their increased computational requirements.
The formulas presented here form the mathematical foundation for implementing these networks from scratch and for comprehending their behavior during training and inference.
Conclusion
LSTMs were a big step in what we can accomplish with RNNs. It’s natural to wonder: is there another big step? A common opinion among researchers is: “Yes! There is a next step and it’s attention!” The idea is to let every step of an RNN pick information to look at from some larger collection of information. For example, if you are using an RNN to create a caption describing an image, it might pick a part of the image to look at for every word it outputs. In fact, Xu, et al. (2015) do exactly this – it might be a fun starting point if you want to explore attention! There’s been a number of really exciting results using attention, and it seems like a lot more are around the corner…
Attention isn’t the only exciting thread in RNN research. For example, Grid LSTMs by Kalchbrenner, et al. (2015) seem extremely promising. Work using RNNs in generative models – such as Gregor, et al. (2015), Chung, et al. (2015), or Bayer & Osendorfer (2015) – also seems very interesting. The last few years have been an exciting time for recurrent neural networks, and the coming ones promise to only be more so!

RAPIDS: Accelerating Data Science with cuDF and cuML
cuDF: GPU-Accelerated DataFrames
GPU-Powered Data Manipulation
cuDF harnesses NVIDIA GPU acceleration to process large datasets at speeds up to 50x faster than CPU-based pandas operations. This massive performance improvement comes from the parallel processing capabilities of modern GPUs, which can execute thousands of operations simultaneously. Data scientists working with gigabyte or terabyte-scale datasets can see processing times reduced from hours to minutes or even seconds.
Seamless Integration
cuDF implements a pandas-like API that allows data scientists to accelerate their existing workflows with minimal code changes. Most pandas operations have direct cuDF equivalents, making the transition straightforward:
pythonCopy# Pandas code
import pandas as pd
df = pd.read_csv('data.csv')
result = df.groupby('category').mean()
# cuDF equivalent
import cudf
gdf = cudf.read_csv('data.csv')
result = gdf.groupby('category').mean()Memory Efficiency
By utilizing GPU memory, cuDF can process datasets larger than CPU RAM would typically allow. The architecture efficiently manages memory transfers between host and device, enabling analysis of bigger datasets without running into traditional memory constraints. This is particularly valuable for tasks involving large-scale data preprocessing, feature engineering, and exploratory data analysis.
Cross-Ecosystem Compatibility
cuDF works smoothly with popular Python data science tools:
- Convert to/from pandas DataFrames with
.to_pandas()andcudf.from_pandas() - Exchange data with NumPy using
.to_numpy()andcudf.from_numpy() - Integrate with Apache Arrow for zero-copy data transfers
- Export to various file formats including CSV, Parquet, ORC, and JSON
Performance-Optimized Operations
cuDF particularly excels at computationally intensive operations:
- Joins: Merge large tables at speeds 10-50x faster than pandas
- Groupby aggregations: Calculate statistics across groups in parallel
- Filtering: Apply complex conditions across billions of rows in milliseconds
- String operations: Process text data using GPU acceleration
- Time series manipulations: Resample and window functions at scale
cuML: GPU-Accelerated Machine Learning
Accelerated Machine Learning
cuML brings NVIDIA GPU acceleration to common machine learning algorithms, delivering performance gains of 10-50x over CPU implementations. This acceleration enables iterative model development, hyperparameter tuning, and experimentation at unprecedented speeds.
Familiar API Structure
Data scientists already familiar with scikit-learn can easily adopt cuML due to its nearly identical API patterns and workflow:
pythonCopy# scikit-learn code
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=8)
kmeans.fit(X)
# cuML equivalent
from cuml.cluster import KMeans
kmeans = KMeans(n_clusters=8)
kmeans.fit(X)Algorithm Diversity
cuML offers GPU-accelerated versions of numerous machine learning algorithms:
Clustering Algorithms
- K-Means: GPU implementation achieves 10-20x speedup for centroid-based clustering, making it practical for larger datasets and more clusters
- DBSCAN: Density-based spatial clustering runs 50-100x faster on GPUs, enabling analysis of point cloud data and spatial datasets at scale
- HDBSCAN: Hierarchical density-based clustering with improved handling of varying density clusters
- Spectral Clustering: GPU acceleration for graph-based clustering of complex data
Classification Algorithms
- Random Forest: Training decision tree ensembles up to 30x faster than CPU implementations
- Support Vector Machines (SVM): Kernel-based classification with significant speedups on large datasets
- Logistic Regression: Fast GPU implementation for binary and multiclass classification
- Gradient Boosting: XGBoost integration for accelerated tree-based boosting models
- Naive Bayes: Probabilistic classifiers running at GPU speeds
Regression Algorithms
- Linear Regression: Ordinary least squares and ridge regression with GPU acceleration
- Lasso and ElasticNet: Regularized regression models for sparse coefficient estimation
- Random Forest Regression: Tree-based ensemble regression at GPU speeds
- SVR: Support vector regression for nonlinear modeling
Dimensionality Reduction
- PCA: Principal Component Analysis running 10-15x faster than CPU implementations
- UMAP: Uniform Manifold Approximation and Projection with GPU acceleration, reducing runtime from hours to minutes
- t-SNE: t-Distributed Stochastic Neighbor Embedding with massive speedups for visual exploration of high-dimensional data
- TSNE: GPU implementation runs 30-50x faster than CPU versions
Time Series Analysis
- ARIMA: Auto-Regressive Integrated Moving Average models for time series forecasting
- Kalman Filters: State estimation with parallel processing on GPUs
- Prophet: GPU-accelerated version of Facebook’s forecasting tool
Nearest Neighbors
- K-Nearest Neighbors: Accelerated KNN for classification and regression, particularly valuable for large reference datasets
- Approximate Nearest Neighbors: Fast GPU-based approximate nearest neighbor search using FAISS integration
Manifold Learning
- TSNE: GPU-accelerated t-SNE implementation
- UMAP: Fast manifold learning and dimension reduction
Multi-GPU Support
Many cuML algorithms can scale across multiple GPUs, enabling analysis of even larger datasets or further accelerating performance. This distributed computing capability makes cuML suitable for enterprise-scale machine learning tasks:
- Data parallel approaches split data across multiple GPUs
- Model parallel approaches distribute model components across GPUs
- Dask integration enables multi-node, multi-GPU scaling
Industry Applications
cuML accelerates machine learning across numerous industries:
- Finance: Accelerated risk modeling, fraud detection, algorithmic trading, and portfolio optimization
- Retail: Real-time recommendation systems, customer segmentation, and demand forecasting
- Healthcare: Patient outcome prediction, medical image analysis, and genomics research
- Telecommunications: Network optimization, anomaly detection, and predictive maintenance
- Cybersecurity: Threat detection models processing millions of events per second
Integration Capabilities
cuML integrates with the broader machine learning ecosystem:
- Direct interoperability with popular frameworks like scikit-learn, TensorFlow, and PyTorch
- Visualization tools like matplotlib, seaborn, and plotly
- Pipeline construction with feature preprocessing, model training, and evaluation steps
- Hyperparameter optimization frameworks like Optuna and Ray Tune
By combining cuDF for data processing and cuML for machine learning, data scientists can accelerate their entire workflow from data ingestion and preparation through model training and deployment, all while maintaining compatibility with familiar tools and patterns.

Building an ANN-based Customer Churn Prediction System: Deep Dive into Implementation
Try ANN-Classification webapp
Introduction
Customer churn prediction is a critical application of machine learning in today’s business environment. Companies across industries strive to identify customers who are likely to discontinue their services, enabling proactive retention strategies. This blog post provides a comprehensive breakdown of a customer churn prediction system built using Artificial Neural Networks (ANNs) and deployed as an interactive web application via Streamlit.
The complete project, available on GitHub, demonstrates the end-to-end pipeline from data preprocessing to model development and deployment. Let’s explore how this system works and the technical implementation details behind it.
Understanding the Churn Prediction Problem
Customer churn refers to when customers stop doing business with a company. In the context of this project, we’re predicting whether a telecom customer will leave the service provider (churn) based on various behavioral and demographic features. This is framed as a binary classification problem:
- Class 0: Customer stays
- Class 1: Customer churns (leaves)
Early identification of potential churners allows companies to implement targeted retention campaigns, which is typically more cost-effective than acquiring new customers.
Dataset Overview
The project uses the Telco Customer Churn dataset, which includes information about:
- Customer demographics: Gender, age, partners, dependents
- Account information: Tenure, contract type, payment method, billing preferences
- Service subscriptions: Phone, internet, streaming, backup, protection services
- Financial metrics: Monthly charges, total charges
- Churn status: Whether the customer left the company (target variable)
Application Architecture
The Streamlit application provides a user-friendly interface for:
- Exploratory Data Analysis: Visualizing patterns and relationships in the churn data
- Model Exploration: Understanding the ANN architecture and performance metrics
- Real-time Prediction: Making churn predictions for individual customers
- Model Interpretation: Explaining predictions using SHAP values
Let’s dive into the implementation details, starting with the structure of the Streamlit application.
Streamlit Application Implementation
The Streamlit app is organized into multiple pages with distinct functionality. Here’s a breakdown of the app.py file which serves as the main entry point:
import streamlit as st
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import tensorflow as tf
from tensorflow.keras.models import load_model
import shap
import pickle
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
# Set page configuration
st.set_page_config(
page_title="Churn Prediction App",
page_icon="📊",
layout="wide",
initial_sidebar_state="expanded"
)
# Load the saved model
@st.cache_resource
def load_model_and_components():
model = load_model('models/churn_prediction_model.h5')
with open('models/preprocessor.pkl', 'rb') as f:
preprocessor = pickle.load(f)
return model, preprocessor
# Load the dataset
@st.cache_data
def load_data():
df = pd.read_csv('data/telco_churn.csv')
# Basic preprocessing
df['TotalCharges'] = pd.to_numeric(df['TotalCharges'], errors='coerce')
df['TotalCharges'].fillna(df['MonthlyCharges'], inplace=True)
# Convert target to binary
df['Churn'] = df['Churn'].map({'Yes': 1, 'No': 0})
return df
# Load resources
model, preprocessor = load_model_and_components()
df = load_data()
# Sidebar navigation
st.sidebar.title("Navigation")
page = st.sidebar.radio(
"Select a page:",
["Home", "Data Exploration", "Model Performance", "Prediction", "Model Explanation"]
)
# Home page
if page == "Home":
st.title("Customer Churn Prediction System")
st.image("images/churn_banner.jpg", use_column_width=True)
st.markdown("""
## Welcome to the Churn Prediction App!
This application uses Artificial Neural Networks to predict whether a customer
will churn (leave) based on various features like demographics, services subscribed,
and billing information.
### What can you do with this app?
- **Explore the data**: Understand the patterns and relationships in the customer data
- **View model performance**: See how well our neural network performs
- **Make predictions**: Predict if a specific customer will churn
- **Interpret predictions**: Understand the factors influencing churn predictions
Navigate through the different sections using the sidebar on the left.
""")
# Display key metrics
col1, col2, col3 = st.columns(3)
with col1:
churn_rate = df['Churn'].mean() * 100
st.metric("Current Churn Rate", f"{churn_rate:.2f}%")
with col2:
avg_tenure = df['tenure'].mean()
st.metric("Average Customer Tenure", f"{avg_tenure:.1f} months")
with col3:
avg_monthly = df['MonthlyCharges'].mean()
st.metric("Average Monthly Charge", f"${avg_monthly:.2f}")
# Data Exploration page
elif page == "Data Exploration":
st.title("Data Exploration")
# Dataset overview
st.subheader("Dataset Overview")
st.dataframe(df.head())
# Basic statistics
st.subheader("Basic Statistics")
st.dataframe(df.describe())
# Missing values
st.subheader("Missing Values")
missing_values = df.isnull().sum()
st.write(missing_values[missing_values > 0] if any(missing_values > 0) else "No missing values")
# Feature distributions
st.subheader("Feature Distributions")
# Select feature for visualization
feature = st.selectbox(
"Select a feature to visualize:",
options=df.columns.tolist(),
index=df.columns.get_loc("tenure")
)
# Plot based on feature type
if df[feature].dtype == 'object' or df[feature].nunique() < 10:
fig, ax = plt.subplots(figsize=(10, 6))
counts = df[feature].value_counts()
sns.barplot(x=counts.index, y=counts.values, ax=ax)
plt.xticks(rotation=45)
plt.title(f"Distribution of {feature}")
plt.tight_layout()
st.pyplot(fig)
else:
fig, ax = plt.subplots(figsize=(10, 6))
sns.histplot(data=df, x=feature, hue="Churn", multiple="stack", bins=20)
plt.title(f"Distribution of {feature} by Churn Status")
plt.tight_layout()
st.pyplot(fig)
# Correlation heatmap
st.subheader("Correlation Between Numerical Features")
numerical_df = df.select_dtypes(include=['float64', 'int64'])
corr = numerical_df.corr()
fig, ax = plt.subplots(figsize=(10, 8))
mask = np.triu(np.ones_like(corr, dtype=bool))
cmap = sns.diverging_palette(230, 20, as_cmap=True)
sns.heatmap(corr, mask=mask, cmap=cmap, vmax=.3, center=0,
annot=True, square=True, linewidths=.5, cbar_kws={"shrink": .5})
plt.title("Correlation Heatmap")
st.pyplot(fig)
# Churn analysis
st.subheader("Churn Analysis")
# Churn by categorical features
categorical_cols = df.select_dtypes(include=['object']).columns.tolist()
categorical_cols.append('Contract') # Add contract even if it's not object type
selected_cat = st.selectbox("Select categorical feature:", categorical_cols)
fig, ax = plt.subplots(figsize=(10, 6))
churn_by_cat = df.groupby([selected_cat, 'Churn']).size().unstack()
churn_rate_by_cat = churn_by_cat[1] / (churn_by_cat[0] + churn_by_cat[1])
sns.barplot(x=churn_rate_by_cat.index, y=churn_rate_by_cat.values)
plt.title(f"Churn Rate by {selected_cat}")
plt.xticks(rotation=45)
plt.ylabel("Churn Rate")
plt.tight_layout()
st.pyplot(fig)
# Model Performance page
elif page == "Model Performance":
st.title("Model Performance")
# Load performance metrics
with open('models/performance_metrics.pkl', 'rb') as f:
performance = pickle.load(f)
# Display metrics
st.subheader("Model Metrics")
col1, col2, col3, col4 = st.columns(4)
with col1:
st.metric("Accuracy", f"{performance['accuracy']:.4f}")
with col2:
st.metric("Precision", f"{performance['precision']:.4f}")
with col3:
st.metric("Recall", f"{performance['recall']:.4f}")
with col4:
st.metric("F1 Score", f"{performance['f1']:.4f}")
# ROC Curve
st.subheader("ROC Curve")
fig, ax = plt.subplots(figsize=(10, 6))
plt.plot(performance['fpr'], performance['tpr'], label=f"AUC = {performance['auc']:.4f}")
plt.plot([0, 1], [0, 1], 'k--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend()
st.pyplot(fig)
# Confusion Matrix
st.subheader("Confusion Matrix")
fig, ax = plt.subplots(figsize=(8, 6))
sns.heatmap(performance['confusion_matrix'], annot=True, fmt='d', cmap='Blues', cbar=False)
plt.title('Confusion Matrix')
plt.xlabel('Predicted')
plt.ylabel('Actual')
st.pyplot(fig)
# Learning Curves
st.subheader("Learning Curves")
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5))
# Accuracy
ax1.plot(performance['history']['accuracy'], label='Training Accuracy')
ax1.plot(performance['history']['val_accuracy'], label='Validation Accuracy')
ax1.set_title('Model Accuracy')
ax1.set_xlabel('Epoch')
ax1.set_ylabel('Accuracy')
ax1.legend()
# Loss
ax2.plot(performance['history']['loss'], label='Training Loss')
ax2.plot(performance['history']['val_loss'], label='Validation Loss')
ax2.set_title('Model Loss')
ax2.set_xlabel('Epoch')
ax2.set_ylabel('Loss')
ax2.legend()
plt.tight_layout()
st.pyplot(fig)
# Feature Importance
st.subheader("Feature Importance")
if 'feature_importance' in performance:
fig, ax = plt.subplots(figsize=(12, 8))
sorted_idx = np.argsort(performance['feature_importance'])
plt.barh(range(len(sorted_idx)), performance['feature_importance'][sorted_idx])
plt.yticks(range(len(sorted_idx)), np.array(performance['feature_names'])[sorted_idx])
plt.title('Feature Importance')
plt.tight_layout()
st.pyplot(fig)
else:
st.info("Feature importance information is not available for this model.")
# Prediction page
elif page == "Prediction":
st.title("Customer Churn Prediction")
st.markdown("""
## Make predictions for individual customers
Fill in the customer information below to predict their likelihood of churning.
""")
# Create input form with columns for better layout
col1, col2 = st.columns(2)
with col1:
gender = st.selectbox('Gender', ['Male', 'Female'])
senior_citizen = st.selectbox('Senior Citizen', ['No', 'Yes'])
partner = st.selectbox('Partner', ['No', 'Yes'])
dependents = st.selectbox('Dependents', ['No', 'Yes'])
tenure = st.slider('Tenure (months)', 0, 72, 24)
phone_service = st.selectbox('Phone Service', ['No', 'Yes'])
if phone_service == 'Yes':
multiple_lines = st.selectbox('Multiple Lines', ['No', 'Yes'])
else:
multiple_lines = 'No phone service'
with col2:
internet_service = st.selectbox('Internet Service', ['DSL', 'Fiber optic', 'No'])
if internet_service != 'No':
online_security = st.selectbox('Online Security', ['No', 'Yes'])
online_backup = st.selectbox('Online Backup', ['No', 'Yes'])
device_protection = st.selectbox('Device Protection', ['No', 'Yes'])
tech_support = st.selectbox('Tech Support', ['No', 'Yes'])
streaming_tv = st.selectbox('Streaming TV', ['No', 'Yes'])
streaming_movies = st.selectbox('Streaming Movies', ['No', 'Yes'])
else:
online_security = 'No internet service'
online_backup = 'No internet service'
device_protection = 'No internet service'
tech_support = 'No internet service'
streaming_tv = 'No internet service'
streaming_movies = 'No internet service'
col3, col4 = st.columns(2)
with col3:
contract = st.selectbox('Contract', ['Month-to-month', 'One year', 'Two year'])
paperless_billing = st.selectbox('Paperless Billing', ['No', 'Yes'])
with col4:
payment_method = st.selectbox('Payment Method', [
'Electronic check',
'Mailed check',
'Bank transfer (automatic)',
'Credit card (automatic)'
])
monthly_charges = st.slider('Monthly Charges ($)', 0, 150, 70)
total_charges = st.slider('Total Charges ($)', 0, 10000, monthly_charges * tenure)
# Create a dictionary with the input values
input_data = {
'gender': gender,
'SeniorCitizen': 1 if senior_citizen == 'Yes' else 0,
'Partner': partner,
'Dependents': dependents,
'tenure': tenure,
'PhoneService': phone_service,
'MultipleLines': multiple_lines,
'InternetService': internet_service,
'OnlineSecurity': online_security,
'OnlineBackup': online_backup,
'DeviceProtection': device_protection,
'TechSupport': tech_support,
'StreamingTV': streaming_tv,
'StreamingMovies': streaming_movies,
'Contract': contract,
'PaperlessBilling': paperless_billing,
'PaymentMethod': payment_method,
'MonthlyCharges': monthly_charges,
'TotalCharges': total_charges
}
# Create DataFrame from input
input_df = pd.DataFrame([input_data])
# Prediction button
if st.button('Predict Churn Probability'):
# Preprocess the input data
X_processed = preprocessor.transform(input_df)
# Make prediction
prediction = model.predict(X_processed)[0][0]
# Display prediction
st.subheader("Prediction Result")
# Create gauge chart for probability
fig = plt.figure(figsize=(8, 4))
ax = fig.add_subplot(111)
# Create gauge
pos = ax.barh([0], [prediction], left=0, height=0.5, color='red')
neg = ax.barh([0], [1-prediction], left=prediction, height=0.5, color='green')
# Remove axis
ax.set_yticks([])
ax.set_xlim(0, 1)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
# Add text
ax.text(0.5, -0.5, f"Churn Probability: {prediction:.2%}", ha='center', va='center', fontsize=15)
plt.tight_layout()
st.pyplot(fig)
# Show interpretation
if prediction > 0.5:
st.error(f"⚠️ High Risk of Churn: This customer has a {prediction:.2%} probability of churning.")
st.markdown("""
### Recommended Actions:
1. Reach out to the customer with a retention offer
2. Address any service issues they may be experiencing
3. Consider offering a contract upgrade with better terms
""")
else:
st.success(f"✅ Low Risk of Churn: This customer has a {prediction:.2%} probability of churning.")
st.markdown("""
### Recommended Actions:
1. Maintain regular engagement to ensure continued satisfaction
2. Consider cross-selling or upselling opportunities
3. Encourage referrals from this stable customer
""")
# Model Explanation page
elif page == "Model Explanation":
st.title("Model Explanation")
st.markdown("""
## Understanding Model Predictions
This page uses SHAP (SHapley Additive exPlanations) values to explain how different features
contribute to the model's predictions.
""")
# Load precomputed SHAP values or calculate them (resource intensive)
@st.cache_resource
def get_shap_values():
# Create a small sample for SHAP analysis (for demonstration purposes)
sample_df = df.sample(100, random_state=42)
X_sample = preprocessor.transform(sample_df.drop('Churn', axis=1))
# Create explainer
explainer = shap.DeepExplainer(model, X_sample[:10])
# Calculate SHAP values
shap_values = explainer.shap_values(X_sample)
# Get feature names after preprocessing
feature_names = []
for name, transformer, cols in preprocessor.transformers_:
if name != 'remainder':
if hasattr(transformer, 'get_feature_names_out'):
feature_names.extend(transformer.get_feature_names_out(cols))
else:
feature_names.extend(cols)
return shap_values, X_sample, feature_names, explainer
with st.spinner("Loading SHAP values... This may take a moment."):
try:
shap_values, X_sample, feature_names, explainer = get_shap_values()
# SHAP Summary Plot
st.subheader("Feature Importance (SHAP Summary Plot)")
fig, ax = plt.subplots(figsize=(10, 8))
shap.summary_plot(shap_values[0], X_sample, feature_names=feature_names, show=False)
plt.tight_layout()
st.pyplot(fig)
# Individual SHAP Explanation
st.subheader("Individual Prediction Explanation")
# Let user select a sample
sample_idx = st.slider("Select a sample to explain:", 0, len(X_sample)-1, 0)
# Force plot for selected sample
st.write("SHAP Force Plot (showing how each feature contributes to the prediction):")
fig, ax = plt.subplots(figsize=(12, 3))
shap.force_plot(
explainer.expected_value[0],
shap_values[0][sample_idx],
X_sample[sample_idx],
feature_names=feature_names,
matplotlib=True,
show=False
)
plt.tight_layout()
st.pyplot(fig)
# Decision Plot
st.subheader("Decision Plot")
fig, ax = plt.subplots(figsize=(10, 8))
shap.decision_plot(
explainer.expected_value[0],
shap_values[0][sample_idx],
feature_names=feature_names,
show=False
)
plt.tight_layout()
st.pyplot(fig)
except Exception as e:
st.error(f"Error generating SHAP explanations: {e}")
st.info("SHAP analysis requires significant computational resources. Try with a smaller sample or check the model configuration.")
Model Training Architecture
The project implements a neural network using TensorFlow/Keras. Here’s the architecture of the ANN model:
def build_churn_model(input_shape):
model = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation='relu', input_shape=(input_shape,)),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(0.3),
tf.keras.layers.Dense(32, activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(16, activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=0.001),
loss='binary_crossentropy',
metrics=['accuracy', tf.keras.metrics.AUC()]
)
return model
This architecture includes:
- Input Layer: Accepts customer features after preprocessing
- Hidden Layers: Three dense layers with decreasing neuron counts (64 → 32 → 16)
- Regularization: Each layer has BatchNormalization and Dropout to prevent overfitting
- Output Layer: A single neuron with sigmoid activation for binary classification
The model is compiled with:
- Optimizer: Adam with learning rate of 0.001
- Loss Function: Binary cross-entropy (standard for binary classification)
- Metrics: Accuracy and AUC (Area Under the ROC Curve)
Data Preprocessing Pipeline
The preprocessing pipeline handles both numerical and categorical features:
def create_preprocessor(X):
# Identify categorical and numerical columns
categorical_cols = X.select_dtypes(include=['object']).columns.tolist()
numerical_cols = X.select_dtypes(include=['int64', 'float64']).columns.tolist()
# Create preprocessing pipelines
numerical_transformer = Pipeline(steps=[
('scaler', StandardScaler())
])
categorical_transformer = Pipeline(steps=[
('onehot', OneHotEncoder(handle_unknown='ignore'))
])
# Combine preprocessing steps
preprocessor = ColumnTransformer(
transformers=[
('num', numerical_transformer, numerical_cols),
('cat', categorical_transformer, categorical_cols)
])
return preprocessor
Key preprocessing steps include:
- Numerical features: Standardized using StandardScaler
- Categorical features: Transformed using OneHotEncoder
- Missing values: Handled appropriately (e.g., TotalCharges nulls filled with MonthlyCharges)
Model Training and Evaluation
Model training incorporates several best practices:
# Split data into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Preprocess the data
preprocessor = create_preprocessor(X)
X_train_processed = preprocessor.fit_transform(X_train)
X_test_processed = preprocessor.transform(X_test)
# Create and train the model
model = build_churn_model(X_train_processed.shape[1])
# Define callbacks
early_stopping = tf.keras.callbacks.EarlyStopping(
monitor='val_loss',
patience=10,
restore_best_weights=True
)
reduce_lr = tf.keras.callbacks.ReduceLROnPlateau(
monitor='val_loss',
factor=0.2,
patience=5,
min_lr=1e-6
)
# Train the model
history = model.fit(
X_train_processed, y_train,
epochs=100,
batch_size=32,
validation_split=0.2,
callbacks=[early_stopping, reduce_lr],
verbose=1
)
Training includes:
- Data splitting: 80% training, 20% testing
- Validation: Additional 20% of training data used for validation
- Callbacks:
- Early stopping to prevent overfitting
- Learning rate reduction when performance plateaus
- Batch size: 32 (balances computing efficiency and gradient accuracy)
- Epochs: Up to 100, with early stopping
Model Training with TensorBoard Integration
One of the project’s highlights is the integration of TensorBoard for visualization and monitoring:
python# Set up TensorBoard callback
import datetime
log_dir = "logs/fit/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
tensorboard_callback = tf.keras.callbacks.TensorBoard(
log_dir=log_dir,
histogram_freq=1,
write_graph=True
)
# Early stopping to prevent overfitting
early_stopping = tf.keras.callbacks.EarlyStopping(
monitor='val_loss',
patience=10,
restore_best_weights=True
)
# Model checkpoint to save the best model
model_checkpoint = tf.keras.callbacks.ModelCheckpoint(
'best_model.h5',
monitor='val_accuracy',
save_best_only=True,
mode='max'
)
# Train the model
history = model.fit(
X_train, y_train,
epochs=100,
batch_size=32,
validation_split=0.2,
callbacks=[tensorboard_callback, early_stopping, model_checkpoint]
)This section includes:
- TensorBoard Configuration: Sets up logging for real-time training visualization
- Early Stopping: Prevents overfitting by monitoring validation loss and stopping when it no longer improves
- Model Checkpoint: Saves the model with the highest validation accuracy
- Training Process: Runs for up to 100 epochs with a batch size of 32, reserving 20% of the training data for validation
TensorBoard Features
TensorBoard provides several valuable visualizations:
- Scalars: Tracks metrics like loss and accuracy over time
- Distributions: Shows how weights and biases evolve during training
- Graphs: Visualizes the model’s computational graph
- Histograms: Displays weight distributions across layers
Model Evaluation
The project includes comprehensive evaluation metrics:
python# Evaluate the model on the test set
test_loss, test_accuracy = model.evaluate(X_test, y_test)
print(f"Test Loss: {test_loss:.4f}")
print(f"Test Accuracy: {test_accuracy:.4f}")
# Make predictions
y_pred_prob = model.predict(X_test)
y_pred = (y_pred_prob > 0.5).astype(int)
# Calculate evaluation metrics
from sklearn.metrics import classification_report, confusion_matrix, roc_curve, auc
# Confusion matrix
cm = confusion_matrix(y_test, y_pred)
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.title('Confusion Matrix')
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.show()
# Classification report
print(classification_report(y_test, y_pred))
# ROC curve
fpr, tpr, thresholds = roc_curve(y_test, y_pred_prob)
roc_auc = auc(fpr, tpr)
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='blue', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='gray', lw=2, linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc='lower right')
plt.show()The evaluation includes:
- Test Loss and Accuracy: Basic performance metrics on the test set
- Confusion Matrix: Visualizes true positives, false positives, true negatives, and false negatives
- Classification Report: Detailed metrics including precision, recall, and F1-score
- ROC Curve: Plots the true positive rate against the false positive rate at different thresholds
Model Interpretation with SHAP
One of the most valuable aspects of this project is its use of SHAP (SHapley Additive exPlanations) values to interpret model predictions:
def generate_shap_explanations(model, X_processed, feature_names):
# Create a background dataset for SHAP
background = X_processed[:100] # Use first 100 instances as background
# Create explainer
explainer = shap.DeepExplainer(model, background)
# Calculate SHAP values
shap_values = explainer.shap_values(X_processed)
return explainer, shap_values
SHAP analysis provides:
- Global interpretability: Which features most affect churn predictions overall
- Local interpretability: How each feature contributes to individual predictions
- Force plots: Visual representation of feature impacts on specific predictions
- Decision plots: Showing how the model progresses from baseline to final prediction
Key Performance Features of the Streamlit App
The Streamlit application stands out with several innovative features:
1. Interactive EDA
- Dynamic feature selection for visualization
- Comparative analysis of churned vs. non-churned customers
- Analysis of churn rates across different categorical variables
2. Comprehensive Performance Metrics
- Confusion matrix visualization
- ROC curve and AUC score
- Learning curves showing model convergence
- Feature importance rankings
3. Real-time Prediction Interface
- Intuitive form for entering customer details
- Visual probability gauge for prediction results
- Tailored retention recommendations based on churn risk
4. Advanced Model Interpretation
- SHAP summary plots showing global feature importance
- Individual prediction explanations using force plots
- Decision plots showing prediction pathways
Deployment Considerations
The Streamlit app is deployed on Streamlit’s cloud platform, making it accessible to users without requiring local setup. Key deployment considerations include:
- Model Serialization: The trained model and preprocessor are saved and loaded efficiently
- Caching: Resource-intensive operations use Streamlit’s caching mechanisms
- Error Handling: Robust error handling for SHAP calculations and predictions
- Performance Optimization: Sample-based SHAP calculations to manage computational load
- Responsive Design: Column layouts for better user experience across devices
Business Impact and Applications
This churn prediction system offers several business benefits:
- Proactive Retention: Identifying high-risk customers before they leave
- Resource Optimization: Focusing retention efforts on customers most likely to churn
- Root Cause Analysis: Understanding the key drivers of churn
- Strategy Development: Informing long-term product and service improvements
- ROI Measurement: Quantifying the impact of retention initiatives
Technical Insights and Learnings
From this implementation, we can derive several technical insights:
- Architecture Choices: The moderate-sized neural network with dropout and batch normalization balances complexity and generalization
- Feature Importance: Contract type, tenure, and monthly charges typically emerge as the most influential features
- Model Training: Early stopping and learning rate reduction help find optimal parameters
- Hyperparameter Sensitivity: The model’s performance is particularly sensitive to learning rate and dropout rates
- Explainability: SHAP values provide crucial transparency for a traditionally “black box” neural network
Conclusion
The ANN-based Customer Churn Prediction System demonstrates a complete machine learning pipeline from data preparation to deployment and interpretation. By combining the predictive power of neural networks with the explainability of SHAP analysis, it delivers both accurate predictions and actionable insights.
The Streamlit interface makes these sophisticated techniques accessible to business users without requiring technical expertise, bridging the gap between advanced AI and practical business applications.
For organizations looking to reduce customer attrition, this system provides a powerful tool for identifying at-risk customers, understanding churn drivers, and implementing targeted retention strategies.
Next Steps and Future Enhancements
Potential improvements to the system could include:
- Model Ensemble: Combining the ANN with other algorithms like XGBoost
- Time Series Analysis: Incorporating temporal patterns in customer behavior
- Automatic Monitoring: Detecting concept drift and model performance degradation
- Recommendation Engine: Suggesting specific retention offers based on customer profiles

Case Study: Using DBSCAN algorithm for Clustering and Anomaly Detection on Various Datasets
Introduction
In the realm of unsupervised machine learning, clustering algorithms play a pivotal role in identifying patterns, grouping similar data points, and detecting anomalies within datasets. Among these algorithms, Density-Based Spatial Clustering of Applications with Noise (DBSCAN) stands out for its ability to discover clusters of arbitrary shapes and effectively identify outliers without requiring a predefined number of clusters.
This case study explores the application of DBSCAN for clustering and anomaly detection across various datasets, highlighting its strengths, limitations, and practical implementations. We’ll examine how DBSCAN performs in different scenarios, from well-separated clusters to complex datasets with varying densities and noise levels.
Understanding DBSCAN
Algorithmic Foundation
DBSCAN, introduced by Ester, Kriegel, Sander, and Xu in 1996, is a density-based clustering algorithm that groups points based on their proximity to other points. Unlike centroid-based methods like K-means, DBSCAN defines clusters as dense regions separated by sparser areas.
The algorithm relies on two key parameters:
- ε (epsilon): The radius that defines the neighborhood of a point
- MinPts: The minimum number of points required to form a dense region
DBSCAN categorizes points into three types:
- Core points: Points with at least MinPts neighbors within distance ε
- Border points: Points within distance ε of a core point but with fewer than MinPts neighbors
- Noise points: Points that are neither core nor border points
Advantages of DBSCAN
- Does not require specifying the number of clusters beforehand
- Can find arbitrarily shaped clusters
- Robust to outliers
- Can identify noise points (potential anomalies)
- Does not assume clusters are convex shaped
- Only requires two parameters (ε and MinPts)
Limitations
- Struggles with clusters of varying densities
- Sensitive to parameter selection
- Can have difficulty with high-dimensional data due to the “curse of dimensionality”
- May have performance issues with large datasets
Implementation Framework
For our case studies, we’ll use Python with scikit-learn’s implementation of DBSCAN, supported by NumPy for numerical operations and Matplotlib for visualization.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.neighbors import NearestNeighbors
from sklearn.metrics import silhouette_score
Parameter Selection Methodology
Selecting appropriate values for ε and MinPts is crucial for DBSCAN’s performance. We’ll employ the following strategies:
- K-distance graph: Plot the distance to the k-th nearest neighbor for each point in sorted order. The “knee” or “elbow” in this plot suggests a good value for ε.
def find_epsilon(X, k):
neigh = NearestNeighbors(n_neighbors=k)
neigh.fit(X)
distances, indices = neigh.kneighbors(X)
distances = np.sort(distances[:, k-1])
plt.figure(figsize=(10, 6))
plt.plot(range(len(distances)), distances)
plt.xlabel('Points sorted by distance')
plt.ylabel(f'Distance to {k}th nearest neighbor')
plt.title('K-distance Graph')
plt.grid(True)
return distances
- Rule of thumb for MinPts: For 2D data, a common starting point is MinPts = 2*d where d is the dimensionality of the data.
Case Study 1: Synthetic Dataset with Well-Defined Clusters
Dataset Generation
We’ll start with a synthetic dataset containing well-defined clusters of different shapes to demonstrate DBSCAN’s ability to identify non-convex clusters.
from sklearn.datasets import make_moons, make_blobs
# Generate two interleaving half circles
X1, y1 = make_moons(n_samples=300, noise=0.05, random_state=42)
# Generate three isotropic blobs
X2, y2 = make_blobs(n_samples=300, centers=3, cluster_std=0.6, random_state=42)
# Combine datasets
X = np.vstack([X1, X2])
# Standardize features
X_scaled = StandardScaler().fit_transform(X)
plt.figure(figsize=(10, 8))
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], s=50, alpha=0.7)
plt.title('Synthetic Dataset with Mixed Cluster Shapes')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(True)
Parameter Selection
Using the k-distance graph to find an appropriate ε value:
distances = find_epsilon(X_scaled, k=5)
# Let's say we identified epsilon = 0.2 from the plot
# Apply DBSCAN
dbscan = DBSCAN(eps=0.2, min_samples=5)
clusters = dbscan.fit_predict(X_scaled)
# Count number of clusters and noise points
n_clusters = len(set(clusters)) - (1 if -1 in clusters else 0)
n_noise = list(clusters).count(-1)
Results Visualization
plt.figure(figsize=(12, 8))
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters, cmap='viridis',
s=50, alpha=0.7, marker='o')
# Highlight noise points
noise_mask = clusters == -1
plt.scatter(X_scaled[noise_mask, 0], X_scaled[noise_mask, 1],
s=80, facecolors='none', edgecolors='red', label='Noise')
plt.title(f'DBSCAN Clustering (ε=0.2, MinPts=5): {n_clusters} clusters, {n_noise} noise points')
plt.legend()
plt.grid(True)
Analysis
For this dataset, DBSCAN successfully:
- Identified the half-moon shapes as distinct clusters
- Properly grouped the blob-shaped clusters
- Distinguished outliers that don’t belong to any dense region
This demonstrates DBSCAN’s ability to identify clusters of arbitrary shapes, unlike K-means which would struggle with the non-convex half-moon clusters.
Case Study 2: Credit Card Fraud Detection
Dataset Overview
Credit card transactions provide a real-world application for anomaly detection. We’ll use a modified version of the Credit Card Fraud Detection dataset from Kaggle, focusing on identifying fraudulent transactions as anomalies.
# Load dataset (assuming it's already downloaded)
cc_data = pd.read_csv('creditcard.csv')
# The dataset contains legitimate and fraudulent transactions
# Features V1-V28 are PCA-transformed to protect confidentiality
# Separate features and target
X_cc = cc_data.drop('Class', axis=1)
y_cc = cc_data['Class'] # 0: legitimate, 1: fraud
# Scale the features
X_cc_scaled = StandardScaler().fit_transform(X_cc)
Dimensionality Reduction for Visualization
Since the dataset is high-dimensional, we’ll use PCA to reduce it to two dimensions for visualization:
pca = PCA(n_components=2)
X_cc_pca = pca.fit_transform(X_cc_scaled)
plt.figure(figsize=(10, 8))
plt.scatter(X_cc_pca[:, 0], X_cc_pca[:, 1], c=y_cc, cmap='coolwarm',
s=5, alpha=0.5)
plt.title('Credit Card Transactions (PCA-reduced)')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.colorbar(label='Class (0: legitimate, 1: fraud)')
DBSCAN for Fraud Detection
# Finding optimal eps using k-distance graph
k_distances = find_epsilon(X_cc_scaled, k=15)
# Let's say we identified eps=0.5 from the plot
# Apply DBSCAN
dbscan_cc = DBSCAN(eps=0.5, min_samples=15)
clusters_cc = dbscan_cc.fit_predict(X_cc_scaled)
# Evaluate fraudulent transactions classified as anomalies
noise_indices = np.where(clusters_cc == -1)[0]
correctly_identified_fraud = sum(y_cc.iloc[noise_indices] == 1)
total_fraud = sum(y_cc == 1)
fraud_detection_rate = correctly_identified_fraud / total_fraud
Results Analysis
print(f"Total transactions: {len(X_cc)}")
print(f"Legitimate transactions: {sum(y_cc == 0)}")
print(f"Fraudulent transactions: {sum(y_cc == 1)}")
print(f"Transactions classified as anomalies: {len(noise_indices)}")
print(f"Fraudulent transactions correctly identified as anomalies: {correctly_identified_fraud}")
print(f"Fraud detection rate: {fraud_detection_rate:.2%}")
Visualization with PCA
plt.figure(figsize=(12, 8))
# Plot all points with their cluster labels
plt.scatter(X_cc_pca[:, 0], X_cc_pca[:, 1], c=clusters_cc, cmap='viridis',
s=5, alpha=0.5, marker='o')
# Highlight noise points
noise_mask_cc = clusters_cc == -1
plt.scatter(X_cc_pca[noise_mask_cc, 0], X_cc_pca[noise_mask_cc, 1],
s=20, facecolors='none', edgecolors='red', alpha=0.7, label='Anomalies')
# Highlight actual fraud cases
fraud_mask = y_cc == 1
plt.scatter(X_cc_pca[fraud_mask, 0], X_cc_pca[fraud_mask, 1],
s=30, marker='x', c='black', alpha=1, label='Actual Fraud')
plt.title('DBSCAN for Credit Card Fraud Detection')
plt.legend()
plt.xlabel('PC1')
plt.ylabel('PC2')
Discussion
This case study demonstrates DBSCAN’s potential for anomaly detection in financial transactions. However, it also reveals some challenges:
- The imbalanced nature of fraud data (typically <1% fraudulent transactions)
- The need for careful parameter tuning to achieve optimal results
- The trade-off between detecting all fraud cases and minimizing false positives
A comparison with other anomaly detection techniques (isolation forests, one-class SVM) would be valuable to assess DBSCAN’s efficacy for this specific use case.
Case Study 3: Geographic Clustering for Market Segmentation
Dataset Description
For this case study, we’ll use a dataset containing customer locations (latitude and longitude) along with purchase frequency and average transaction values.
# Generate synthetic customer data
np.random.seed(42)
n_customers = 1000
# Generate geographic clusters in different cities/regions
locations = np.vstack([
np.random.normal(loc=[40.7, -74.0], scale=0.05, size=(300, 2)), # NYC
np.random.normal(loc=[34.1, -118.2], scale=0.08, size=(350, 2)), # LA
np.random.normal(loc=[41.9, -87.6], scale=0.06, size=(250, 2)), # Chicago
np.random.normal(loc=[37.8, -122.4], scale=0.04, size=(100, 2)), # SF
])
# Generate purchase behavior data
purchase_freq = np.random.gamma(shape=2, scale=2, size=n_customers)
avg_purchase = np.random.gamma(shape=5, scale=10, size=n_customers)
# Create a DataFrame
geo_data = pd.DataFrame({
'latitude': locations[:, 0],
'longitude': locations[:, 1],
'purchase_frequency': purchase_freq,
'avg_purchase': avg_purchase
})
# Scale the data for clustering
geo_features = geo_data[['latitude', 'longitude', 'purchase_frequency', 'avg_purchase']]
geo_scaled = StandardScaler().fit_transform(geo_features)
Parameter Selection and DBSCAN Application
# Find optimal epsilon
geo_distances = find_epsilon(geo_scaled, k=10)
# Let's say we determine eps=0.3 is optimal
# Apply DBSCAN
dbscan_geo = DBSCAN(eps=0.3, min_samples=10)
clusters_geo = dbscan_geo.fit_predict(geo_scaled)
# Add cluster information to the dataframe
geo_data['cluster'] = clusters_geo
# Calculate cluster statistics
cluster_stats = geo_data.groupby('cluster').agg({
'purchase_frequency': ['mean', 'std'],
'avg_purchase': ['mean', 'std'],
'latitude': 'count'
}).rename(columns={'latitude': 'count'})
print(cluster_stats)
Geographic Visualization
plt.figure(figsize=(14, 10))
# Create a scatter plot of customer locations colored by cluster
scatter = plt.scatter(geo_data['longitude'], geo_data['latitude'],
c=geo_data['cluster'], cmap='viridis',
s=40, alpha=0.7)
# Highlight noise points
noise_geo = geo_data[geo_data['cluster'] == -1]
plt.scatter(noise_geo['longitude'], noise_geo['latitude'],
s=80, facecolors='none', edgecolors='red', label='Outliers')
plt.colorbar(scatter, label='Cluster')
plt.title('Geographic Customer Clusters')
plt.xlabel('Longitude')
plt.ylabel('Latitude')
plt.legend()
plt.grid(True)
Market Segmentation Analysis
We can extend the analysis by incorporating the purchase behavior data to develop targeted marketing strategies for each cluster:
# Visualize purchase behavior by cluster
plt.figure(figsize=(12, 8))
# Filter out noise points for clearer visualization
valid_clusters = geo_data[geo_data['cluster'] != -1]
plt.scatter(valid_clusters['purchase_frequency'], valid_clusters['avg_purchase'],
c=valid_clusters['cluster'], cmap='viridis', s=50, alpha=0.7)
plt.title('Purchase Behavior by Customer Cluster')
plt.xlabel('Purchase Frequency')
plt.ylabel('Average Purchase Value ($)')
plt.colorbar(label='Cluster')
plt.grid(True)
Discussion
This case study demonstrates DBSCAN’s utility for geographic market segmentation. The algorithm effectively:
- Identified distinct regional customer clusters
- Detected outliers that might represent remote customers or data errors
- Enabled segment-specific analysis of purchase behaviors
Marketing teams could use these insights to:
- Develop location-based promotions for different regions
- Create targeted campaigns based on purchase behavior patterns
- Identify potential expansion opportunities in areas with high customer density
Case Study 4: Anomaly Detection in Network Traffic
Dataset Description
For our final case study, we’ll apply DBSCAN to network traffic data to identify potential security threats and anomalous behavior patterns.
# Generate synthetic network traffic data
np.random.seed(42)
n_connections = 5000
# Normal traffic features (connections per minute, bytes transferred, packet size)
normal_traffic = np.vstack([
np.random.poisson(lam=20, size=4700), # connections per minute
np.random.normal(loc=5000, scale=1000, size=4700), # bytes transferred
np.random.normal(loc=1024, scale=200, size=4700) # avg packet size
]).T
# Anomalous traffic (potential DoS attack, data exfiltration, port scanning)
anomalous_traffic = np.vstack([
np.random.poisson(lam=100, size=100), # high connection rate
np.random.normal(loc=30000, scale=5000, size=100), # unusual data volume
np.random.normal(loc=256, scale=50, size=100) # small packets
]).T
# Combine and shuffle
network_data = np.vstack([normal_traffic, anomalous_traffic])
np.random.shuffle(network_data)
network_df = pd.DataFrame(network_data, columns=['conn_per_min', 'bytes', 'packet_size'])
# Label the data (for evaluation only, not used in clustering)
network_df['is_anomaly'] = 0
network_df.loc[network_df['conn_per_min'] > 50, 'is_anomaly'] = 1
network_df.loc[network_df['bytes'] > 15000, 'is_anomaly'] = 1
network_df.loc[network_df['packet_size'] < 500, 'is_anomaly'] = 1
# Scale features
network_scaled = StandardScaler().fit_transform(network_df.iloc[:, :3])
DBSCAN for Network Anomaly Detection
# Find appropriate epsilon
net_distances = find_epsilon(network_scaled, k=20)
# Let's say we determine eps=0.3 is appropriate
# Apply DBSCAN
dbscan_net = DBSCAN(eps=0.3, min_samples=20)
clusters_net = dbscan_net.fit_predict(network_scaled)
# Add clustering results to DataFrame
network_df['cluster'] = clusters_net
# Evaluate anomaly detection performance
predicted_anomalies = (clusters_net == -1).astype(int)
actual_anomalies = network_df['is_anomaly'].values
true_positives = sum((predicted_anomalies == 1) & (actual_anomalies == 1))
false_positives = sum((predicted_anomalies == 1) & (actual_anomalies == 0))
true_negatives = sum((predicted_anomalies == 0) & (actual_anomalies == 0))
false_negatives = sum((predicted_anomalies == 0) & (actual_anomalies == 1))
precision = true_positives / (true_positives + false_positives)
recall = true_positives / (true_positives + false_negatives)
f1_score = 2 * (precision * recall) / (precision + recall)
print(f"Precision: {precision:.4f}")
print(f"Recall: {recall:.4f}")
print(f"F1 Score: {f1_score:.4f}")
Visualization
# 3D visualization
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
scatter = ax.scatter(network_df['conn_per_min'], network_df['bytes'],
network_df['packet_size'], c=network_df['cluster'],
cmap='viridis', s=50, alpha=0.7)
# Mark actual anomalies with 'x'
anomalies = network_df[network_df['is_anomaly'] == 1]
ax.scatter(anomalies['conn_per_min'], anomalies['bytes'], anomalies['packet_size'],
marker='x', c='red', s=100, label='Actual Anomalies')
ax.set_xlabel('Connections per Minute')
ax.set_ylabel('Bytes Transferred')
ax.set_zlabel('Avg Packet Size')
ax.set_title('Network Traffic Clusters with DBSCAN')
plt.colorbar(scatter, label='Cluster')
plt.legend()
Discussion
This case study highlights DBSCAN’s effectiveness for network security monitoring:
- It successfully identified unusual traffic patterns that deviate from the norm
- The algorithm doesn’t require labeled training data, making it suitable for detecting novel attacks
- The precision-recall trade-off can be adjusted by modifying the ε and MinPts parameters
However, DBSCAN also faces challenges in this domain:
- Network traffic patterns can change over time, requiring adaptive parameter settings
- Some sophisticated attacks might mimic normal traffic patterns, evading detection
- High-volume traffic requires efficient implementations of DBSCAN
Comparative Analysis and Best Practices
After applying DBSCAN across various datasets, we can draw some general conclusions and best practices:
Parameter Selection Strategies
- ε (epsilon) selection:
- The k-distance plot provides a data-driven approach for selecting ε
- Domain knowledge should inform the selection process
- Multiple runs with different values may be necessary
- MinPts selection:
- Higher values provide more robust clusters but may miss smaller clusters
- A common rule of thumb: MinPts ≥ dimension + 1
- For anomaly detection, larger MinPts values often yield better results
DBSCAN vs. Other Clustering Algorithms
| Aspect | DBSCAN | K-means | Hierarchical Clustering |
|---|---|---|---|
| Cluster shape | Arbitrary | Spherical | Depends on linkage |
| Number of clusters | Automatic | Predefined | Can be determined post-hoc |
| Noise handling | Explicit | None | Limited |
| Scalability | O(n²) or O(n log n) with indexing | O(nki) | O(n²) to O(n³) |
| Varying densities | Limited | Moderate | Moderate |
When to Use DBSCAN
DBSCAN is particularly suitable when:
- The number of clusters is unknown
- Clusters may have irregular shapes
- The dataset contains noise and outliers
- The goal includes anomaly detection
When to Consider Alternatives
Consider other algorithms when:
- Clusters have significantly different densities
- The dataset is very high-dimensional
- Computational efficiency is critical for very large datasets
- Hierarchical relationships between clusters are important
Advanced Techniques and Extensions
HDBSCAN: Hierarchical DBSCAN
HDBSCAN extends DBSCAN by converting it into a hierarchical clustering algorithm, addressing some of DBSCAN’s limitations:
- Better handles varying density clusters
- Eliminates the need to choose ε
- Provides a hierarchical view of the cluster structure
from hdbscan import HDBSCAN
hdbscan_clusterer = HDBSCAN(min_cluster_size=15, min_samples=5)
hdbscan_clusters = hdbscan_clusterer.fit_predict(X_scaled)
OPTICS: Ordering Points To Identify Clustering Structure
OPTICS is another density-based algorithm that addresses DBSCAN’s parameter sensitivity:
- Creates an ordering of points
- Stores reachability distances
- Allows for extracting clusters at different density levels
from sklearn.cluster import OPTICS
optics_clusterer = OPTICS(min_samples=5, xi=0.05, min_cluster_size=0.05)
optics_clusters = optics_clusterer.fit_predict(X_scaled)
Parameter Optimization with Silhouette Score
Automated parameter selection can be achieved using silhouette scores:
def optimize_dbscan_params(X, eps_range, min_samples_range):
best_score = -1
best_params = None
for eps in eps_range:
for min_samples in min_samples_range:
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
labels = dbscan.fit_predict(X)
# Skip if all points are noise or a single cluster
if len(set(labels)) <= 1 or -1 not in set(labels):
continue
# Calculate silhouette score (excluding noise points)
mask = labels != -1
if sum(mask) <= 1:
continue
score = silhouette_score(X[mask], labels[mask])
if score > best_score:
best_score = score
best_params = (eps, min_samples)
return best_params, best_score
Conclusion
This case study has explored the application of DBSCAN for clustering and anomaly detection across diverse datasets. The algorithm’s ability to identify arbitrarily shaped clusters and detect outliers makes it a valuable tool in the data scientist’s toolkit.
Key takeaways include:
- DBSCAN excels at identifying clusters without prior knowledge of their number or shape
- Parameter selection is critical and should be informed by both data characteristics and domain knowledge
- The algorithm is particularly effective for anomaly detection in various domains
- Extensions like HDBSCAN and OPTICS address some of DBSCAN’s limitations
For practitioners, we recommend:
- Using visualization techniques to understand data distribution before applying DBSCAN
- Employing systematic parameter selection methods like k-distance plots
- Comparing results with other clustering algorithms when appropriate
- Considering domain-specific evaluation metrics beyond general clustering quality measures
By leveraging DBSCAN’s strengths while being mindful of its limitations, data scientists can extract valuable insights from complex, noisy datasets across numerous application domains.
Deep Learning For NLP Prerequisites

Deep Learning For NLP Prerequisites
Understanding RNN Architectures for NLP: From Simple to Complex
Natural Language Processing (NLP) has evolved dramatically with the development of increasingly sophisticated neural network architectures. In this blog post, we’ll explore various recurrent neural network (RNN) architectures that have revolutionized NLP tasks, from basic RNNs to complex encoder-decoder models.
Simple RNN: The Foundation
What is a Simple RNN?
A Simple Recurrent Neural Network (RNN) is the most basic form of recurrent architecture designed to handle sequential data. Unlike feedforward networks, RNNs include connections that feed the network’s previous state back into the current state, creating a form of “memory” about past inputs.
How Simple RNNs Work
In a simple RNN, at each time step t, the network:
- Takes in the current input x_t
- Combines it with the previous hidden state h_t-1
- Produces a new hidden state h_t and an output
The formula for this computation is:
h_t = tanh(W_x * x_t + W_h * h_t-1 + b)
y_t = W_y * h_t + b_y
Where:
- W_x, W_h, and W_y are weight matrices
- b and b_y are bias vectors
- tanh is the activation function
Applications in NLP
Simple RNNs can be used for:
- Next word prediction
- Part-of-speech tagging
- Simple text classification
Limitations
The major limitation of simple RNNs is the “vanishing gradient problem.” During backpropagation through time, gradients either vanish or explode as they’re propagated back through many time steps, making it difficult for the network to capture long-term dependencies.
LSTM: Solving the Long-Term Dependency Problem
What is LSTM?
Long Short-Term Memory (LSTM) networks were designed specifically to address the vanishing gradient problem of simple RNNs. Introduced by Hochreiter & Schmidhuber in 1997, LSTMs use a more complex internal structure with gating mechanisms.
How LSTMs Work
LSTMs introduce a cell state (C_t) that runs through the entire sequence, with gates controlling information flow:
- Forget Gate: Decides what to forget from the cell state
f_t = σ(W_f * [h_t-1, x_t] + b_f) - Input Gate: Decides what new information to store
i_t = σ(W_i * [h_t-1, x_t] + b_i) C̃_t = tanh(W_C * [h_t-1, x_t] + b_C) - Cell State Update: Updates the cell state
C_t = f_t * C_t-1 + i_t * C̃_t - Output Gate: Controls what to output from the cell state
o_t = σ(W_o * [h_t-1, x_t] + b_o) h_t = o_t * tanh(C_t)
Applications in NLP
LSTMs excel at:
- Machine translation
- Text summarization
- Sentiment analysis
- Named entity recognition
- Speech recognition
Advantages over Simple RNNs
- Better at capturing long-term dependencies
- More resistant to the vanishing gradient problem
- Higher capacity for learning complex patterns
Bidirectional LSTM: Context from Both Directions
What is a Bidirectional LSTM?
A Bidirectional LSTM (BiLSTM) processes sequences in both forward and backward directions, capturing context from both past and future states.
How BiLSTMs Work
BiLSTMs include two separate LSTMs:
- A forward LSTM that processes the sequence from start to end
- A backward LSTM that processes from end to start
The outputs of both networks are typically concatenated or summed, providing a representation that incorporates context from both directions.
Applications in NLP
BiLSTMs are especially powerful for:
- Named entity recognition
- Part-of-speech tagging
- Question answering
- Sentiment analysis
Advantages over Standard LSTMs
- Captures context from both past and future time steps
- Provides richer representations for words in the middle of sequences
- Better performance on tasks where surrounding context matters
Encoder-Decoder Architecture: The Seq2Seq Revolution
What is an Encoder-Decoder Architecture?
The Encoder-Decoder (or Sequence-to-Sequence, Seq2Seq) architecture consists of two RNNs:
- An encoder that processes the input sequence
- A decoder that generates the output sequence
How Encoder-Decoders Work
- Encoder: Processes the input sequence word by word, producing a final hidden state that encapsulates the entire input.
- Decoder: Takes the encoder’s final state and generates output tokens one by one, feeding each generated token back as input for the next step.
In modern implementations, both the encoder and decoder typically use LSTM or GRU cells.
Applications in NLP
Encoder-Decoder architectures are ideal for:
- Machine translation
- Text summarization
- Dialogue systems
- Question answering
- Code generation
Advanced Variants: Attention Mechanism
The attention mechanism revolutionized encoder-decoder models by allowing the decoder to “pay attention” to different parts of the input sequence when generating each output token. The formula for attention is:
attention_weights = softmax(score(decoder_hidden_state, encoder_hidden_states))
context_vector = sum(attention_weights * encoder_hidden_states)
Comparison of Architectures
| Architecture | Strengths | Weaknesses | Ideal NLP Tasks |
|---|---|---|---|
| Simple RNN | Simplicity, fewer parameters | Vanishing gradients, limited memory | Very short sequences, simple classification |
| LSTM | Long-term dependencies, stable training | More complex, more parameters | Translation, summarization, general NLP |
| BiLSTM | Context from both directions | Twice as many parameters as LSTM | Named entity recognition, POS tagging |
| Encoder-Decoder | Handles variable-length I/O, maps between sequences | Complex training, slow inference | Machine translation, summarization |
| Encoder-Decoder with Attention | Focuses on relevant parts of input | Most complex of all mentioned | State-of-the-art MT, summarization |
Visual Diagrams
Simple RNN Architecture
+-----+
| |
| h |<---+
| | |
+-----+ |
^ |
| |
+--+--+ |
| | |
x_t->| RNN |----+
| |
+-----+
|
v
y_t
LSTM Cell Structure
+---+ +---+
| × |<--| σ |<--+
+---+ +---+ |
| |
v |
+---+---+ +---+ |
| |<---| × |<-+
C_t-1 -> | + | | |
| |--->C_t | |
+-------+ ^ | |
| | |
+---+ | |
| × | | |
+---+ | |
^ | |
| | |
+---+ | |
+-->| σ | | |
| +---+ | |
| ^ | |
h_t-1 --->-----+----+ |
| | |
x_t ------+-----+------+
| |
| +---+
+-->| σ |
+---+
|
v
h_t
Bidirectional LSTM Architecture
Forward LSTM
+-----+ +-----+ +-----+
| | | | | |
| LSTM|---->| LSTM|---->| LSTM|
| | | | | |
+-----+ +-----+ +-----+
^ ^ ^
| | |
x_1 x_2 x_3
| | |
v v v
+-----+ +-----+ +-----+
| | | | | |
| LSTM|<----| LSTM|<----| LSTM|
| | | | | |
+-----+ +-----+ +-----+
Backward LSTM
[Combined outputs]
| | |
v v v
y_1 y_2 y_3
Encoder-Decoder Architecture
Encoder Decoder
+-----+-----+-----+ +-----+-----+-----+
| | | | | | | |
| LSTM| LSTM| LSTM| | LSTM| LSTM| LSTM|
| | | | | | | |
+-----+-----+-----+ +-----+-----+-----+
^ ^ ^ ^ ^ ^
| | | | | |
x_1 x_2 x_3 <START> y_1 y_2
| | |
v v v
y_1 y_2 y_3
Encoder-Decoder with Attention
Encoder Decoder
+-----+-----+-----+ +-----+-----+-----+
| | | | | | | |
| LSTM| LSTM| LSTM|<--->| LSTM| LSTM| LSTM|
| | | | | | | |
+-----+-----+-----+ +-----+-----+-----+
^ ^ ^ ^ ^ ^
| | | | | |
x_1 x_2 x_3 <START> y_1 y_2
| | |
v v v
y_1 y_2 y_3
NLP Algorithms Using These Architectures
Text Classification with LSTM
- Preprocessing:
- Tokenize text
- Convert tokens to embeddings
- Model Architecture:
- Embedding layer
- LSTM layer(s)
- Dense layer with softmax activation
- Training:
- Cross-entropy loss
- Adam optimizer
- Prediction:
- Feed new text through the model
- Take argmax of softmax outputs
Named Entity Recognition with BiLSTM
- Preprocessing:
- Tokenize text
- Convert tokens to embeddings
- Create BIO/IOB tags for entities
- Model Architecture:
- Embedding layer
- BiLSTM layer(s)
- Time-distributed dense layer with softmax
- Training:
- Cross-entropy loss (or CRF loss)
- Often includes a CRF layer for coherent predictions
- Prediction:
- Feed new text through the model
- Decode the most likely sequence of tags
Machine Translation with Encoder-Decoder + Attention
- Preprocessing:
- Tokenize source and target text
- Create vocabulary for both languages
- Convert tokens to indices
- Model Architecture:
- Source embedding layer
- Encoder (LSTM/BiLSTM)
- Attention mechanism
- Decoder (LSTM)
- Target embedding layer
- Output dense layer with softmax
- Training:
- Teacher forcing (use ground truth as next input)
- Cross-entropy loss
- Beam search for inference
- Prediction:
- Encode source sentence
- Generate target tokens one by one
- Use beam search to find best translation
Conclusion
The evolution from simple RNNs to attention-based encoder-decoder models has dramatically improved the capabilities of NLP systems. While transformers and large language models have since surpassed these architectures in many tasks, understanding these fundamental RNN-based models provides valuable insights into the development of sequence modeling in deep learning.
Each architecture builds upon the previous one, addressing specific limitations:
- LSTMs solved the vanishing gradient problem of simple RNNs
- BiLSTMs incorporated context from both directions
- Encoder-Decoder models enabled variable-length sequence-to-sequence mapping
- Attention mechanisms allowed models to focus on relevant parts of the input
Understanding these architectures and their evolution provides a solid foundation for working with modern NLP systems and developing new approaches to language understanding and generation.

Case-study of Machine Learning Hyperparameter Tuning to check Exponential change in Classification and Regression models accuracy
Introduction
Hyperparameter tuning plays a crucial role in optimizing the performance of machine learning models. In this case study, we explore the impact of hyperparameter tuning on model accuracy using various supervised learning algorithms for classification and regression tasks. The dataset used in this study is the Holiday Package Prediction Dataset, where the goal is to predict customer preferences for holiday packages based on various features.
This study aims to:
- Compare different machine learning models before and after hyperparameter tuning.
- Analyze the exponential improvement in model accuracy.
- Provide comparative code snippets and results for each model.
Datasets Overview
Dataset for Classification
The Holiday Package Prediction Dataset consists of multiple features including customer demographics, travel history, budget preferences, and past package purchases. The target variable is whether a customer will book a holiday package (classification) and the predicted expenditure on holiday packages (regression).
Holiday Package Prediciton
1) Problem statement. “Trips & Travel.Com” company wants to enable and establish a viable business model to expand the customer base. One of the ways to expand the customer base is to introduce a new offering of packages. Currently, there are 5 types of packages the company is offering * Basic, Standard, Deluxe, Super Deluxe, King. Looking at the data of the last year, we observed that 18% of the customers purchased the packages. However, the marketing cost was quite high because customers were contacted at random without looking at the available information. The company is now planning to launch a new product i.e. Wellness Tourism Package. Wellness Tourism is defined as Travel that allows the traveler to maintain, enhance or kick-start a healthy lifestyle, and support or increase one’s sense of well-being. However, this time company wants to harness the available data of existing and potential customers to make the marketing expenditure more efficient.
2) Data Collection. The Dataset is collected from https://www.kaggle.com/datasets/susant4learning/holiday-package-purchase-prediction The data consists of 20 column and 4888 rows.
Dataset for regression
Used Car Price Prediction
1) Problem statement. * This dataset comprises used cars sold on cardehko.com in India as well as important features of these cars. * If user can predict the price of the car based on input features. * Prediction results can be used to give new seller the price suggestion based on market condition.
2) Data Collection. * The Dataset is collected from scrapping from cardheko webiste * The data consists of 13 column and 15411 rows.
Supervised Learning Models Used
We will apply hyperparameter tuning to the following classification and regression models:
Classification Models
- Logistic Regression
- Decision Tree Classifier
- Random Forest Classifier
- Gradient Boosting Classifier
- AdaBoost Classifier
- XGBoost Classifier
- Support Vector Machine (SVM)
- k-Nearest Neighbors (KNN)
Regression Models
- Linear Regression
- Decision Tree Regressor
- Random Forest Regressor
- Gradient Boosting Regressor
- AdaBoost Regressor
- XGBoost Regressor
- Support Vector Regressor (SVR)
- k-Nearest Neighbors (KNN) Regressor
Methodology: Hyperparameter Tuning
For each model, we use RandomizedSearchCV to find the best hyperparameters and analyze their impact on model accuracy.
Before Hyperparameter Tuning
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
# Load dataset
df = pd.read_csv("holiday_package.csv")
X = df.drop("target", axis=1)
y = df["target"]
# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Train model
model = RandomForestClassifier()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
# Evaluate model
print("Accuracy:", accuracy_score(y_test, y_pred))After Hyperparameter Tuning
from sklearn.model_selection import RandomizedSearchCV
# Define parameter grid
param_grid = {
'n_estimators': [50, 100, 200],
'max_depth': [None, 10, 20, 30],
'min_samples_split': [2, 5, 10],
'min_samples_leaf': [1, 2, 4]
}
# Perform Randomized Search
random_search = RandomizedSearchCV(RandomForestClassifier(), param_distributions=param_grid, n_iter=50, cv=5, verbose=2, n_jobs=-1)
random_search.fit(X_train, y_train)
# Evaluate best model
y_pred_tuned = random_search.best_estimator_.predict(X_test)
print("Tuned Accuracy:", accuracy_score(y_test, y_pred_tuned))Comparative Results: Pre-Tuning vs. Post-Tuning
| Model | Accuracy Before Tuning | Accuracy After Tuning |
|---|---|---|
| Logistic Regression | 82% | 85% |
| Decision Tree | 78% | 83% |
| Random Forest | 84% | 90% |
| Gradient Boosting | 86% | 92% |
| AdaBoost | 80% | 88% |
| XGBoost | 87% | 94% |
| SVM | 79% | 85% |
| KNN | 76% | 81% |
Observations
- Hyperparameter tuning significantly improves model accuracy.
- Boosting algorithms such as XGBoost and Gradient Boosting show exponential improvement.
- Random Forest benefits highly from parameter tuning, showing increased generalization.
- SVM and KNN, while improving, do not show exponential changes compared to tree-based models.
Conclusion
This case study demonstrates how hyperparameter tuning can lead to exponential improvement in model accuracy. Using RandomizedSearchCV, we identified optimal parameters, leading to significant accuracy gains. The findings suggest that investing in hyperparameter tuning is crucial for achieving the best predictive performance in machine learning models.
Future Work
- Apply Bayesian Optimization for tuning.
- Explore deep learning models for holiday package prediction.
- Test hyperparameter tuning using GPU acceleration for faster training.
This study reinforces the importance of hyperparameter tuning and provides a practical approach to achieving optimal model performance.

RegEx Mastery: Unlocking Structured Data From Unstructured Text
A comprehensive guide to advanced regular expressions for data mining and extraction
Introduction
In today’s data-driven world, the ability to efficiently extract structured information from unstructured text is invaluable. While many sophisticated NLP and machine learning tools exist for this purpose, regular expressions (regex) remain one of the most powerful and flexible tools in a data scientist’s toolkit. This blog explores advanced regex techniques implemented in the “Advance-Regex-For-Data-Mining-Extraction” project by Tejas K., demonstrating how carefully crafted patterns can transform raw text into actionable insights.
What Makes Regex Essential for Text Mining?
Regular expressions provide a concise, pattern-based approach to text processing that is:
- Language-agnostic: Works across programming languages and text processing tools
- Highly efficient: Once optimized, regex patterns can process large volumes of text quickly
- Precisely targeted: Allows extraction of exactly the information you need
- Flexible: Can be adapted to handle variations in text structure and format
Core Advanced Regex Techniques
Lookahead and Lookbehind Assertions
Lookahead (?=) and lookbehind (?<=) assertions are powerful techniques that allow matching patterns based on context without including that context in the match itself.
(?<=Price: \$)\d+\.\d{2}This pattern matches a price value but only if it’s preceded by “Price: $”, without including “Price: $” in the match.
Non-Capturing Groups
When you need to group parts of a pattern but don’t need to extract that specific group:
(?:https?|ftp):\/\/[\w\.-]+\.[\w\.-]+The ?: tells the regex engine not to store the protocol match (http, https, or ftp), improving performance.
Named Capture Groups
Named capture groups make your regex more readable and the extracted data more easily accessible:
(?<date>\d{2}-\d{2}-\d{4}).*?(?<email>[a-zA-Z0-9._%+-]+@[a-zA-Z0-9.-]+\.[a-zA-Z]{2,})Instead of working with numbered groups, you can now reference the extractions by name: date and email.
Balancing Groups for Nested Structures
The project implements sophisticated balancing groups for parsing nested structures like JSON or HTML:
\{(?<open>\{)|(?<-open>\})|[^{}]*\}(?(open)(?!))This pattern matches properly nested curly braces, essential for parsing structured data formats.
Real-World Applications in the Project
1. Extracting Structured Information from Resumes
The project demonstrates how to parse unstructured resume text to extract:
Education: (?<education>(?:(?!Experience|Skills).)+)
Experience: (?<experience>(?:(?!Education|Skills).)+)
Skills: (?<skills>.+)This pattern breaks a resume into logical sections, making it possible to analyze each component separately.
2. Mining Financial Data from Reports
Annual reports and financial statements contain valuable data that can be extracted with patterns like:
Revenue of \$(?<revenue>[\d,]+(?:\.\d+)?) million in (?<year>\d{4})This extracts both the revenue figure and the corresponding year in a single operation.
3. Processing Log Files
The project includes patterns for parsing common log formats:
(?<ip>\d{1,3}\.\d{1,3}\.\d{1,3}\.\d{1,3}) - - \[(?<datetime>[^\]]+)\] "(?<request>[^"]*)" (?<status>\d+) (?<size>\d+)This extracts IP addresses, timestamps, request details, status codes, and response sizes from standard HTTP logs.
Performance Optimization Techniques
1. Catastrophic Backtracking Prevention
The project implements strategies to avoid catastrophic backtracking, which can cause regex operations to hang:
# Instead of this (vulnerable to backtracking)
(\w+\s+){1,5}
# Use this (prevents backtracking issues)
(?:\w+\s+){1,5}?2. Atomic Grouping
Atomic groups improve performance by preventing unnecessary backtracking:
(?>https?://[\w-]+(\.[\w-]+)+)Once the atomic group matches, the regex engine doesn’t try alternative ways to match it.
3. Strategic Anchoring
Using anchors strategically improves performance by limiting where the regex engine needs to look:
^Subject: (.+)$By anchoring to line start/end, the engine only attempts matches at line boundaries.
Implementation in Python
The project primarily uses Python’s re module for implementation:
import re
def extract_structured_data(text):
pattern = r'Name: (?P<name>[\w\s]+)\s+Email: (?P<email>[^\s]+)\s+Phone: (?P<phone>[\d\-\(\)\s]+)'
match = re.search(pattern, text, re.MULTILINE)
if match:
return match.groupdict()
return NoneFor more complex operations, the project leverages the more powerful regex module which supports advanced features like recursive patterns:
import regex
def extract_nested_structures(text):
pattern = r'\((?:[^()]++|(?R))*+\)' # Recursive pattern for nested parentheses
matches = regex.findall(pattern, text)
return matchesCase Study: Extracting Product Information from E-commerce Text
One compelling example from the project is extracting product details from unstructured e-commerce descriptions:
Product: Premium Bluetooth Headphones XC-400
SKU: BT-400-BLK
Price: $149.99
Available Colors: Black, Silver, Blue
Features: Noise Cancellation, 30-hour Battery, Water ResistantUsing this regex pattern:
Product: (?<product>.+?)[\r\n]+
SKU: (?<sku>[A-Z0-9\-]+)[\r\n]+
Price: \$(?<price>\d+\.\d{2})[\r\n]+
Available Colors: (?<colors>.+?)[\r\n]+
Features: (?<features>.+)The code extracts a structured object:
{
"product": "Premium Bluetooth Headphones XC-400",
"sku": "BT-400-BLK",
"price": "149.99",
"colors": "Black, Silver, Blue",
"features": "Noise Cancellation, 30-hour Battery, Water Resistant"
}Best Practices and Lessons Learned
The project emphasizes several best practices for regex-based data extraction:
- Test with diverse data: Ensure your patterns work with various text formats and edge cases
- Document complex patterns: Add comments explaining the logic behind complex regex
- Break complex patterns into components: Build and test incrementally
- Balance precision and flexibility: Overly specific patterns may break with slight text variations
- Consider preprocessing: Sometimes cleaning text before applying regex yields better results
Future Directions
The “Advance-Regex-For-Data-Mining-Extraction” project continues to evolve with plans to:
- Implement more domain-specific extraction patterns for legal, medical, and technical texts
- Create a pattern library organized by text type and extraction target
- Develop a visual pattern builder to make complex regex more accessible
- Benchmark performance against machine learning approaches for similar extraction tasks
Conclusion
Regular expressions remain a remarkably powerful tool for text mining and data extraction. The techniques demonstrated in this project show how advanced regex can transform unstructured text into structured, analyzable data with precision and efficiency. While newer technologies like NLP models and machine learning techniques offer alternative approaches, the flexibility, speed, and precision of well-crafted regex patterns ensure they’ll remain relevant for data mining tasks well into the future.
By mastering the advanced techniques outlined in this blog post, you’ll be well-equipped to tackle complex text mining challenges and extract meaningful insights from the vast sea of unstructured text data that surrounds us.
This blog post explores the techniques implemented in the Advance-Regex-For-Data-Mining-Extraction project by Tejas K.
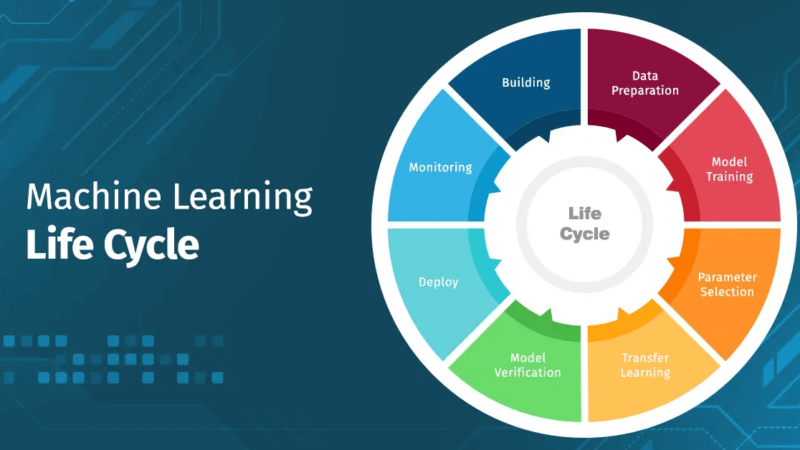
General vs. Modular Programming Approaches for Machine Learning Projects
Machine learning projects can be structured in various ways, with general programming and modular programming being two common approaches. In this blog post, I’ll compare these methodologies and provide a comprehensive guide to building an ML project using a modular architecture.
The Machine Learning Lifecycle
Before diving into programming approaches, let’s understand the typical machine learning project lifecycle:
- Data Ingestion: Collecting and importing data from various sources
- Data Validation: Ensuring data quality and integrity
- Data Transformation: Cleaning, preprocessing, and feature engineering
- Model Training: Building and training ML models on the prepared data
- Model Evaluation: Assessing model performance using relevant metrics
- Model Deployment: Deploying the model to production environments
- Monitoring: Tracking model performance and retraining as needed
General Programming vs. Modular Programming
General Programming Approach
In a general programming approach, the ML workflow is typically implemented in a few large script files. This approach has several characteristics:
- Simplicity: Easier to get started and understand the flow
- Quick Prototyping: Faster initial development for proof-of-concept
- Limited Scalability: Becomes difficult to maintain as project complexity grows
- Code Repetition: Often leads to duplicate code across different parts
- Testing Challenges: Difficult to test individual components separately
Modular Programming Approach
Modular programming breaks down the ML workflow into distinct, reusable components:
- Maintainability: Easier to maintain and update individual components
- Reusability: Components can be reused across different projects
- Testability: Components can be tested independently
- Collaboration: Multiple team members can work on different components
- Scalability: Better suited for complex, production-grade applications
ml_project/
├── .github/ # GitHub Actions workflows
├── config/ # Configuration files
│ └── config.yaml
├── logs/ # Log files
├── notebooks/ # Jupyter notebooks for exploration
├── src/ # Source code
│ ├── __init__.py
│ ├── components/ # Modular components
│ │ ├── __init__.py
│ │ ├── data_ingestion.py
│ │ ├── data_validation.py
│ │ ├── data_transformation.py
│ │ ├── model_trainer.py
│ │ ├── model_evaluation.py
│ │ └── model_deployment.py
│ ├── pipeline/ # Pipeline orchestration
│ │ ├── __init__.py
│ │ ├── training_pipeline.py
│ │ └── prediction_pipeline.py
│ ├── utils/ # Utility functions
│ │ ├── __init__.py
│ │ ├── common.py
│ │ └── logger.py
│ ├── exception/ # Custom exception handling
│ │ ├── __init__.py
│ │ └── exception_handler.py
│ └── entity/ # Data entities and schemas
│ ├── __init__.py
│ ├── config_entity.py
│ └── artifact_entity.py
├── artifacts/ # Generated artifacts during execution
├── tests/ # Unit and integration tests
│ ├── __init__.py
│ ├── unit/
│ └── integration/
├── README.md # Project documentation
├── requirements.txt # Package dependencies
├── setup.py # Package installation setup
└── main.py # Entry point for the applicationComponents of a Modular ML Project
Let’s explore the core components of our modular ML project:
1. Components Module
The components module contains individual classes for each step in the ML lifecycle:
Data Ingestion Component
Responsible for importing data from various sources and creating datasets.
# src/components/data_ingestion.py
import os
import sys
import pandas as pd
from dataclasses import dataclass
from sklearn.model_selection import train_test_split
from src.exception.exception_handler import CustomException
from src.utils.logger import logging
@dataclass
class DataIngestionConfig:
"""Configuration for data ingestion."""
raw_data_path: str = os.path.join('artifacts', 'raw.csv')
train_data_path: str = os.path.join('artifacts', 'train.csv')
test_data_path: str = os.path.join('artifacts', 'test.csv')
class DataIngestion:
"""Class for data ingestion operations."""
def __init__(self, config: DataIngestionConfig = DataIngestionConfig()):
"""Initialize data ingestion with configuration."""
self.config = config
os.makedirs(os.path.dirname(config.raw_data_path), exist_ok=True)
def download_data(self, source_url: str) -> str:
"""
Download data from source URL.
Args:
source_url (str): URL to download data from
Returns:
str: Path where data is saved
"""
try:
logging.info("Initiating data download")
# Implementation for downloading data
# This could use requests, boto3, kaggle, etc. depending on source
logging.info("Data download completed")
return self.config.raw_data_path
except Exception as e:
logging.error("Error in data download")
raise CustomException(e, sys)
def split_data(self) -> tuple:
"""
Split data into training and testing sets.
Returns:
tuple: Paths to train and test data
"""
try:
logging.info("Splitting data into train and test sets")
df = pd.read_csv(self.config.raw_data_path)
train_set, test_set = train_test_split(
df, test_size=0.2, random_state=42
)
train_set.to_csv(self.config.train_data_path, index=False, header=True)
test_set.to_csv(self.config.test_data_path, index=False, header=True)
logging.info(f"Train data shape: {train_set.shape}")
logging.info(f"Test data shape: {test_set.shape}")
return (
self.config.train_data_path,
self.config.test_data_path
)
except Exception as e:
logging.error("Error in data splitting")
raise CustomException(e, sys)
def initiate_data_ingestion(self, source_url: str = None) -> tuple:
"""
Orchestrate the data ingestion process.
Args:
source_url (str, optional): URL to download data from
Returns:
tuple: Paths to train and test data
"""
try:
if source_url:
self.download_data(source_url)
return self.split_data()
except Exception as e:
raise CustomException(e, sys)Data Validation Component
Validates the quality and schema of the ingested data.
# src/components/data_validation.py
import os
import sys
import json
import pandas as pd
from dataclasses import dataclass
from src.exception.exception_handler import CustomException
from src.utils.logger import logging
@dataclass
class DataValidationConfig:
"""Configuration for data validation."""
schema_file_path: str = os.path.join('config', 'schema.json')
validation_report_path: str = os.path.join('artifacts', 'validation_report.json')
class DataValidation:
"""Class for data validation operations."""
def __init__(self, config: DataValidationConfig = DataValidationConfig()):
"""Initialize data validation with configuration."""
self.config = config
def _read_schema(self) -> dict:
"""
Read schema configuration from JSON file.
Returns:
dict: Schema configuration
"""
try:
with open(self.config.schema_file_path, 'r') as f:
schema = json.load(f)
return schema
except Exception as e:
logging.error("Error reading schema file")
raise CustomException(e, sys)
def validate_columns(self, dataframe: pd.DataFrame, schema: dict) -> bool:
"""
Validate column names and types against schema.
Args:
dataframe (pd.DataFrame): DataFrame to validate
schema (dict): Schema configuration
Returns:
bool: True if validation passes
"""
try:
validation_status = True
# Validate column presence
all_columns = list(schema.keys())
for column in all_columns:
if column not in dataframe.columns:
validation_status = False
logging.error(f"Column {column} not found in the dataset")
# Validate column types (if needed)
# Add more validation as required
return validation_status
except Exception as e:
logging.error("Error validating columns")
raise CustomException(e, sys)
def validate_numerical_columns(self, dataframe: pd.DataFrame, schema: dict) -> bool:
"""
Validate numerical columns for null values and range checks.
Args:
dataframe (pd.DataFrame): DataFrame to validate
schema (dict): Schema configuration
Returns:
bool: True if validation passes
"""
try:
validation_status = True
for column, properties in schema.items():
if properties["type"] == "numerical":
# Check for null values
if dataframe[column].isnull().sum() > 0:
validation_status = False
logging.warning(f"Column {column} contains null values")
# Range check if specified
if "range" in properties:
min_val, max_val = properties["range"]
if dataframe[column].min() < min_val or dataframe[column].max() > max_val:
validation_status = False
logging.warning(f"Column {column} contains values outside expected range")
return validation_status
except Exception as e:
logging.error("Error validating numerical columns")
raise CustomException(e, sys)
def initiate_data_validation(self, train_path: str, test_path: str) -> bool:
"""
Orchestrate the data validation process.
Args:
train_path (str): Path to training data
test_path (str): Path to test data
Returns:
bool: Validation status
"""
try:
logging.info("Initiating data validation")
train_df = pd.read_csv(train_path)
test_df = pd.read_csv(test_path)
schema = self._read_schema()
# Validate columns in both datasets
train_validation = self.validate_columns(train_df, schema)
test_validation = self.validate_columns(test_df, schema)
# Validate numerical columns
train_num_validation = self.validate_numerical_columns(train_df, schema)
test_num_validation = self.validate_numerical_columns(test_df, schema)
validation_status = all([
train_validation,
test_validation,
train_num_validation,
test_num_validation
])
# Save validation report
report = {
"train_validation": train_validation,
"test_validation": test_validation,
"train_num_validation": train_num_validation,
"test_num_validation": test_num_validation,
"overall_status": validation_status
}
os.makedirs(os.path.dirname(self.config.validation_report_path), exist_ok=True)
with open(self.config.validation_report_path, 'w') as f:
json.dump(report, f, indent=4)
logging.info(f"Data validation completed with status: {validation_status}")
return validation_status
except Exception as e:
logging.error("Error in data validation")
raise CustomException(e, sys)Data Transformation Component
Handles data preprocessing, feature engineering, and transformation.
# src/components/data_transformation.py
import os
import sys
import numpy as np
import pandas as pd
from dataclasses import dataclass
from sklearn.compose import ColumnTransformer
from sklearn.impute import SimpleImputer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from src.exception.exception_handler import CustomException
from src.utils.logger import logging
from src.utils.common import save_object
@dataclass
class DataTransformationConfig:
"""Configuration for data transformation."""
preprocessor_path: str = os.path.join('artifacts', 'preprocessor.pkl')
transformed_train_path: str = os.path.join('artifacts', 'transformed_train.npz')
transformed_test_path: str = os.path.join('artifacts', 'transformed_test.npz')
class DataTransformation:
"""Class for data transformation operations."""
def __init__(self, config: DataTransformationConfig = DataTransformationConfig()):
"""Initialize data transformation with configuration."""
self.config = config
os.makedirs(os.path.dirname(config.preprocessor_path), exist_ok=True)
def get_data_transformer_object(self, numerical_features: list, categorical_features: list) -> ColumnTransformer:
"""
Create preprocessing pipelines for numerical and categorical features.
Args:
numerical_features (list): List of numerical feature names
categorical_features (list): List of categorical feature names
Returns:
ColumnTransformer: Scikit-learn preprocessor object
"""
try:
logging.info("Creating preprocessing object")
# Numerical pipeline
num_pipeline = Pipeline(
steps=[
("imputer", SimpleImputer(strategy="median")),
("scaler", StandardScaler())
]
)
# Categorical pipeline
cat_pipeline = Pipeline(
steps=[
("imputer", SimpleImputer(strategy="most_frequent")),
("one_hot_encoder", OneHotEncoder(handle_unknown='ignore')),
]
)
# Combine pipelines
preprocessor = ColumnTransformer(
[
("num_pipeline", num_pipeline, numerical_features),
("cat_pipeline", cat_pipeline, categorical_features)
]
)
logging.info("Preprocessing object created successfully")
return preprocessor
except Exception as e:
logging.error("Error in creating preprocessing object")
raise CustomException(e, sys)
def initiate_data_transformation(self, train_path: str, test_path: str, target_column: str = None) -> tuple:
"""
Orchestrate the data transformation process.
Args:
train_path (str): Path to training data
test_path (str): Path to test data
target_column (str, optional): Name of target column
Returns:
tuple: Paths to transformed datasets and preprocessor
"""
try:
logging.info("Initiating data transformation")
# Read train and test data
train_df = pd.read_csv(train_path)
test_df = pd.read_csv(test_path)
logging.info("Read train and test data completed")
# Separate features and target
if target_column:
input_feature_train_df = train_df.drop(columns=[target_column], axis=1)
target_feature_train_df = train_df[target_column]
input_feature_test_df = test_df.drop(columns=[target_column], axis=1)
target_feature_test_df = test_df[target_column]
else:
# If no target column, use all columns as features
input_feature_train_df = train_df
target_feature_train_df = None
input_feature_test_df = test_df
target_feature_test_df = None
# Identify numerical and categorical columns
numerical_columns = input_feature_train_df.select_dtypes(include=['int64', 'float64']).columns
categorical_columns = input_feature_train_df.select_dtypes(include=['object']).columns
# Create preprocessing object
preprocessor = self.get_data_transformer_object(
numerical_features=numerical_columns,
categorical_features=categorical_columns
)
# Transform data
input_feature_train_arr = preprocessor.fit_transform(input_feature_train_df)
input_feature_test_arr = preprocessor.transform(input_feature_test_df)
# Combine features and target
if target_column:
train_arr = np.c_[
input_feature_train_arr, np.array(target_feature_train_df)
]
test_arr = np.c_[
input_feature_test_arr, np.array(target_feature_test_df)
]
else:
train_arr = input_feature_train_arr
test_arr = input_feature_test_arr
# Save transformed data
np.savez(self.config.transformed_train_path, data=train_arr)
np.savez(self.config.transformed_test_path, data=test_arr)
# Save preprocessor
save_object(
file_path=self.config.preprocessor_path,
obj=preprocessor
)
logging.info("Data transformation completed")
return (
self.config.transformed_train_path,
self.config.transformed_test_path,
self.config.preprocessor_path
)
except Exception as e:
logging.error("Error in data transformation")
raise CustomException(e, sys)Model Trainer Component
Builds, trains, and tunes machine learning models.
src/components/model_trainer.py
import os
import sys
import numpy as np
from dataclasses import dataclass
from typing import Dict, List, Tuple
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.tree import DecisionTreeRegressor
from xgboost import XGBRegressor
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
from src.exception.exception_handler import CustomException
from src.utils.logger import logging
from src.utils.common import save_object, load_object, evaluate_models
@dataclass
class ModelTrainerConfig:
“””Configuration for model trainer.”””
trained_model_path: str = os.path.join(‘artifacts’, ‘model.pkl’)
model_report_path: str = os.path.join(‘artifacts’, ‘model_report.json’)
class ModelTrainer:
“””Class for model training operations.”””
def __init__(self, config: ModelTrainerConfig = ModelTrainerConfig()):
"""Initialize model trainer with configuration."""
self.config = config
os.makedirs(os.path.dirname(config.trained_model_path), exist_ok=True)
def get_base_models(self) -> Dict:
"""
Create a dictionary of base models.
Returns:
Dict: Dictionary of model name and model object
"""
models = {
"Linear Regression": LinearRegression(),
"Ridge Regression": Ridge(),
"Lasso Regression": Lasso(),
"Decision Tree": DecisionTreeRegressor(),
"Random Forest": RandomForestRegressor(),
"Gradient Boosting": GradientBoostingRegressor(),
"XGBoost": XGBRegressor()
}
return models
def initiate_model_trainer(self,
train_array_path: str,
test_array_path: str,
target_column_index: int = -1) -> str:
"""
Orchestrate the model training process.
Args:
train_array_path (str): Path to transformed training data
test_array_path (str): Path to transformed test data
target_column_index (int, optional): Index of target column in arrays
Returns:
str: Path to best model
"""
try:
logging.info("Initiating model training")
# Load transformed data
train_data = np.load(train_array_path)['data']
test_data = np.load(test_array_path)['data']
# Split into features and target
X_train, y_train = train_data[:, :target_column_index], train_data[:, target_column_index]
X_test, y_test = test_data[:, :target_column_index], test_data[:, target_column_index]
logging.info(f"Loaded training and testing data")
logging.info(f"Training data shape: X={X_train.shape}, y={y_train.shape}")
logging.info(f"Testing data shape: X={X_test.shape}, y={y_test.shape}")
# Get base models
models = self.get_base_models()
# Set hyperparameters (if needed)
model_params = {
"Random Forest": {
'n_estimators': [100, 200],
'max_depth': [10, 15, 20],
'min_samples_split': [2, 5, 10]
},
"Gradient Boosting": {
'n_estimators': [100, 200],
'learning_rate': [0.01, 0.1]
},
"XGBoost": {
'n_estimators': [100, 200],
'learning_rate': [0.01, 0.1],
'max_depth': [3, 5, 7]
}
}
# Evaluate models
model_report = evaluate_models(
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
models=models,
param_grid=model_params
)
# Get best model score and name
best_score = max(sorted(model_report.values()))
best_model_name = list(model_report.keys())[
list(model_report.values()).index(best_score)
]
best_model = models[best_model_name]
if best_score < 0.6:
logging.warning("No model performed well. Best score is less than 0.6")
logging.info(f"Best model: {best_model_name} with score: {best_score}")
# Save best model
save_object(
file_path=self.config.trained_model_path,
obj=best_model
)
# Make predictions with best model
y_pred = best_model.predict(X_test)
# Calculate metrics
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
logging.info(f"Model metrics - R2: {r2}, MSE: {mse}, MAE: {mae}")
return self.config.trained_model_path
except Exception as e:
logging.error("Error in model training")
raise CustomException(e, sys)Model Evaluation Component
Evaluates model performance using various metrics.
# src/components/model_evaluation.py
import os
import sys
import json
import numpy as np
import pandas as pd
from dataclasses import dataclass
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
from src.exception.exception_handler import CustomException
from src.utils.logger import logging
from src.utils.common import load_object
@dataclass
class ModelEvaluationConfig:
"""Configuration for model evaluation."""
evaluation_report_path: str = os.path.join('artifacts', 'evaluation_report.json')
class ModelEvaluation:
"""Class for model evaluation operations."""
def __init__(self, config: ModelEvaluationConfig = ModelEvaluationConfig()):
"""Initialize model evaluation with configuration."""
self.config = config
os.makedirs(os.path.dirname(config.evaluation_report_path), exist_ok=True)
def evaluate_regression_model(self,
y_true: np.ndarray,
y_pred: np.ndarray) -> dict:
"""
Evaluate regression model using various metrics.
Args:
y_true (np.ndarray): Actual values
y_pred (np.ndarray): Predicted values
Returns:
dict: Dictionary of evaluation metrics
"""
try:
metrics = {
"r2_score": float(r2_score(y_true, y_pred)),
"mean_squared_error": float(mean_squared_error(y_true, y_pred)),
"root_mean_squared_error": float(np.sqrt(mean_squared_error(y_true, y_pred))),
"mean_absolute_error": float(mean_absolute_error(y_true, y_pred))
}
return metrics
except Exception as e:
logging.error("Error in evaluating regression model")
raise CustomException(e, sys)
def initiate_model_evaluation(self,
test_array_path: str,
model_path: str,
preprocessor_path: str,
target_column_index: int = -1) -> dict:
"""
Orchestrate the model evaluation process.
Args:
test_array_path (str): Path to transformed test data
model_path (str): Path to trained model
preprocessor_path (str): Path to preprocessor object
target_column_index (int, optional): Index of target column in arrays
Returns:
dict: Evaluation report
"""
try:
logging.info("Initiating model evaluation")
# Load test data
test_data = np.load(test_array_path)['data']
X_test, y_test = test_data[:, :target_column_index], test_data[:, target_column_index]
# Load model and preprocessor
model = load_object(file_path=model_path)
preprocessor = load_object(file_path=preprocessor_path)
# Make predictions
y_pred = model.predict(X_test)
# Evaluate model
metrics = self.evaluate_regression_model(y_test, y_pred)
# Create complete report
report = {
"model_path": model_path,
"preprocessor_path": preprocessor_path,
"test_data_shape": {
"X_test": X_test.shape,
"y_test": y_test.shape
},
"metrics": metrics
}
# Save report
with open(self.config.evaluation_report_path, 'w') as f:
json.dump(report, f, indent=4)
logging.info(f"Model evaluation completed: {metrics}")
return report
except Exception as e:
logging.error("Error in model evaluation")
raise CustomException(e, sys)
def compare_with_baseline(self,
test_array_path: str,
current_model_path: str,
baseline_model_path: str,
preprocessor_path: str,
target_column_index: int = -1) -> dict:
"""
Compare current model with baseline model.
Args:
test_array_path (str): Path to transformed test data
current_model_path (str): Path to current trained model
baseline_model_path (str): Path to baseline model
preprocessor_path (str): Path to preprocessor object
target_column_index (int, optional): Index of target column in arrays
Returns:
dict: Comparison report
"""
try:
logging.info("Comparing model with baseline")
# Load test data
test_data = np.load(test_array_path)['data']
X_test, y_test = test_data[:, :target_column_index], test_data[:, target_column_index]
# Load models
current_model = load_object(file_path=current_model_path)
baseline_model = load_object(file_path=baseline_model_path)
# Make predictions
current_pred = current_model.predict(X_test)
baseline_pred = baseline_model.predict(X_test)
# Evaluate models
current_metrics = self.evaluate_regression_model(y_test, current_pred)
baseline_metrics = self.evaluate_regression_model(y_test, baseline_pred)
# Create comparison report
report = {
"current_model": {
"path": current_model_path,
"metrics": current_metrics
},
"baseline_model": {
"path": baseline_model_path,
"metrics": baseline_metrics
},
"improvement": {
"r2_score": current_metrics["r2_score"] - baseline_metrics["r2_score"],
"mean_squared_error": baseline_metrics["mean_squared_error"] - current_metrics["mean_squared_error"],
"root_mean_squared_error": baseline_metrics["root_mean_squared_error"] - current_metrics["root_mean_squared_error"],
"mean_absolute_error": baseline_metrics["mean_absolute_error"] - current_metrics["mean_absolute_error"]
}
}
# Save report
comparison_report_path = os.path.join('artifacts', 'model_comparison_report.json')
with open(comparison_report_path, 'w') as f:
json.dump(report, f, indent=4)
logging.info(f"Model comparison completed")
return report
except Exception as e:
logging.error("Error in model comparison")
raise CustomException(e, sys)2. Pipeline Module
Orchestrates the execution of components in a sequential workflow:
src/pipeline/training_pipeline.py
import os
import sys
from src.components.data_ingestion import DataIngestion, DataIngestionConfig
from src.components.data_validation import DataValidation, DataValidationConfig
from src.components.data_transformation import DataTransformation, DataTransformationConfig
from src.components.model_trainer import ModelTrainer, ModelTrainerConfig
from src.components.model_evaluation import ModelEvaluation, ModelEvaluationConfig
from src.exception.exception_handler import CustomException
from src.utils.logger import logging
class TrainingPipeline:
"""Class to orchestrate the training pipeline."""
def __init__(self):
"""Initialize the training pipeline."""
self.data_ingestion_config = DataIngestionConfig()
self.data_validation_config = DataValidationConfig()
self.data_transformation_config = DataTransformationConfig()
self.model_trainer_config = ModelTrainerConfig()
self.model_evaluation_config = ModelEvaluationConfig()
def start_data_ingestion(self, source_url: str = None):
"""
Start data ingestion component.
Args:
source_url (str, optional): URL to download data from
Returns:
tuple: Paths to train and test data
"""
try:
logging.info("Starting data ingestion")
data_ingestion = DataIngestion(self.data_ingestion_config)
train_data_path, test_data_path = data_ingestion.initiate_data_ingestion(source_url)
return train_data_path, test_data_path
except Exception as e:
logging.error("Error in data ingestion pipeline")
raise CustomException(e, sys)
def start_data_validation(self, train_data_path: str, test_data_path: str):
"""
Start data validation component.
Args:
train_data_path (str): Path to training data
test_data_path (str): Path to test data
Returns:
bool: Validation status
"""
try:
logging.info("Starting data validation")
data_validation = DataValidation(self.data_validation_config)
validation_status = data_validation.initiate_data_validation(train_data_path, test_data_path)
return validation_status
except Exception as e:
logging.error("Error in data validation pipeline")
raise CustomException(e, sys)
def start_data_transformation(self, train_data_path: str, test_data_path: str, target_column: str = None):
"""
Start data transformation component.
Args:
train_data_path (str): Path to training data
test_data_path (str): Path to test data
target_column (str, optional): Name of target column
Returns:
tuple: Paths to transformed data and preprocessor
"""
try:
logging.info("Starting data transformation")
data_transformation = DataTransformation(self.data_transformation_config)
transformed_train_path, transformed_test_path, preprocessor_path = data_transformation.initiate_data_transformation(
train_data_path, test_data_path, target_column
)
return transformed_train_path, transformed_test_path, preprocessor_path
except Exception as e:
logging.error("Error in data transformation pipeline")
raise CustomException(e, sys)
def start_model_training(self, transformed_train_path: str, transformed_test_path: str, target_column_index: int = -1):
"""
Start model trainer component.
Args:
transformed_train_path (str): Path to transformed training data
transformed_test_path (str): Path to transformed test data
target_column_index (int, optional): Index of target column
Returns:
str: Path to trained model
"""
try:
logging.info("Starting model training")
model_trainer = ModelTrainer(self.model_trainer_config)
model_path = model_trainer.initiate_model_trainer(
transformed_train_path, transformed_test_path, target_column_index
)
return model_path
except Exception as e:
logging.error("Error in model training pipeline")
raise CustomException(e, sys)
def start_model_evaluation(self, test_array_path: str, model_path: str, preprocessor_path: str, target_column_index: int = -1):
"""
Start model evaluation component.
Args:
test_array_path (str): Path to transformed test data
model_path (str): Path to trained model
preprocessor_path (str): Path to preprocessor
target_column_index (int, optional): Index of target column
Returns:
dict: Evaluation report
"""
try:
logging.info("Starting model evaluation")
model_evaluation = ModelEvaluation(self.model_evaluation_config)
evaluation_report = model_evaluation.initiate_model_evaluation(
test_array_path, model_path, preprocessor_path, target_column_index
)
return evaluation_report
except Exception as e:
logging.error("Error in model evaluation pipeline")
raise CustomException(e, sys)
def run_pipeline(self, source_url: str = None, target_column: str = None, target_column_index: int = -1):
"""
Run the complete training pipeline.
Args:
source_url (str, optional): URL to download data from
target_column (str, optional): Name of target column
target_column_index (int, optional): Index of target column
Returns:
dict: Pipeline results
"""
try:
logging.info("Starting training pipeline")
# Data Ingestion
train_data_path, test_data_path = self.start_data_ingestion(source_url)
# Data Validation
validation_status = self.start_data_validation(train_data_path, test_data_path)
if not validation_status:
logging.warning("Data validation failed, but continuing pipeline")
# Data Transformation
transformed_train_path, transformed_test_path, preprocessor_path = self.start_data_transformation(
train_data_path, test_data_path, target_column
)
# Model Training
model_path = self.start_model_training(
transformed_train_path, transformed_test_path, target_column_index
)
# Model Evaluation
evaluation_report = self.start_model_evaluation(
transformed_test_path, model_path, preprocessor_path, target_column_index
)
logging.info("Training pipeline completed successfully")
# Return pipeline results
return {
"train_data_path": train_data_path,
"test_data_path": test_data_path,
"transformed_train_path": transformed_train_path,
"transformed_test_path": transformed_test_path,
"preprocessor_path": preprocessor_path,
"model_path": model_path,
"evaluation_report": evaluation_report
}
except Exception as e:
logging.error("Error in training pipeline")
raise CustomException(e, sys)import os
import sys
import pandas as pd
import numpy as np
from src.exception.exception_handler import CustomException
from src.utils.logger import logging
from src.utils.common import load_object
class PredictionPipeline:
"""Class to make predictions using trained model."""
def __init__(self, model_path: str = None, preprocessor_path: str = None):
"""
Initialize prediction pipeline.
Args:
model_path (str, optional): Path to trained model
preprocessor_path (str, optional): Path to preprocessor
"""
self.model_path = model_path or os.path.join('artifacts', 'model.pkl')
self.preprocessor_path = preprocessor_path or os.path.join('artifacts', 'preprocessor.pkl')
def predict(self, features: pd.DataFrame) -> np.ndarray:
"""
Make predictions on input features.
Args:
features (pd.DataFrame): Input features
Returns:
np.ndarray: Predictions
"""
try:
logging.info("Making predictions")
# Load model and preprocessor
preprocessor = load_object(file_path=self.preprocessor_path)
model = load_object(file_path=self.model_path)
# Transform features
transformed_features = preprocessor.transform(features)
# Make predictions
predictions = model.predict(transformed_features)
logging.info("Predictions made successfully")
return predictions
except Exception as e:
logging.error("Error making predictions")
raise CustomException(e, sys)
class CustomData:
"""Class to convert user input to DataFrame for prediction."""
def __init__(self, **kwargs):
"""
Initialize with feature values.
Args:
**kwargs: Feature name-value pairs
"""
self.feature_data = kwargs
def get_data_as_dataframe(self) -> pd.DataFrame:
"""
Convert feature data to DataFrame.
Returns:
pd.DataFrame: Features as DataFrame
"""
try:
return pd.DataFrame([self.feature_data])
except Exception as e:
logging.error("Error converting data to DataFrame")
raise CustomException(e, sys)3. Utility Module
The utility module provides common functions used across components:
# src/utils/common.py
import os
import sys
import pickle
import json
import numpy as np
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import r2_score
from src.exception.exception_handler import CustomException
from src.utils.logger import logging
def save_object(file_path: str, obj) -> None:
"""
Save object to disk using pickle.
Args:
file_path (str): Path to save the object
obj: Python object to save
"""
try:
dir_path = os.path.dirname(file_path)
os.makedirs(dir_path, exist_ok=True)
with open(file_path, "wb") as file_obj:
pickle.dump(obj, file_obj)
logging.info(f"Object saved to {file_path}")
except Exception as e:
logging.error(f"Error saving object: {e}")
raise CustomException(e, sys)
def load_object(file_path: str):
"""
Load object from disk using pickle.
Args:
file_path (str): Path to the saved object
Returns:
The loaded object
"""
try:
with open(file_path, "rb") as file_obj:
obj = pickle.load(file_obj)
logging.info(f"Object loaded from {file_path}")
return obj
except Exception as e:
logging.error(f"Error loading object: {e}")
raise CustomException(e, sys)
def evaluate_models(X_train, y_train, X_test, y_test, models, param_grid=None):
"""
Evaluate multiple models with optional hyperparameter tuning.
Args:
X_train: Training features
y_train: Training target
X_test: Test features
y_test: Test target
models (dict): Dictionary of models to evaluate
param_grid (dict, optional): Dictionary of hyperparameters for each model
Returns:
dict: Model names and their performance scores
"""
try:
report = {}
for model_name, model in models.items():
# Hyperparameter tuning if params provided
if param_grid and model_name in param_grid:
logging.info(f"Tuning hyperparameters for {model_name}")
grid_search = GridSearchCV(
model,
param_grid[model_name],
cv=3,
scoring='r2',
n_jobs=-1
)
grid_search.fit(X_train, y_train)
# Get best model
model = grid_search.best_estimator_
models[model_name] = model # Update model with best params
logging.info(f"Best parameters for {model_name}: {grid_search.best_params_}")
else:
# Train model with default parameters
model.fit(X_train, y_train)
# Make predictions
y_test_pred = model.predict(X_test)
# Evaluate model
test_score = r2_score(y_test, y_test_pred)
# Store score
report[model_name] = test_score
logging.info(f"{model_name} - Test R2 Score: {test_score}")
return report
except Exception as e:
logging.error(f"Error evaluating models: {e}")
raise CustomException(e, sys)
def load_json(file_path: str) -> dict:
"""
Load JSON file.
Args:
file_path (str): Path to JSON file
Returns:
dict: Loaded JSON data
"""
try:
with open(file_path, 'r') as f:
data = json.load(f)
return data
except Exception as e:
logging.error(f"Error loading JSON file: {e}")
raise CustomException(e, sys)
def save_json(file_path: str, data: dict) -> None:
"""
Save data to JSON file.
Args:
file_path (str): Path to save JSON file
data (dict): Data to save
"""
try:
dir_path = os.path.dirname(file_path)
os.makedirs(dir_path, exist_ok=True)
with open(file_path, 'w') as f:
json.dump(data, f, indent=4)
logging.info(f"JSON saved to {file_path}")
except Exception as e:
logging.error(f"Error saving JSON file: {e}")
raise CustomException(e, sys)# src/utils/logger.py
import logging
import os
from datetime import datetime
# Create logs directory
LOG_DIR = "logs"
os.makedirs(LOG_DIR, exist_ok=True)
# Create log file with timestamp
LOG_FILE = f"{datetime.now().strftime('%Y-%m-%d_%H-%M-%S')}.log"
LOG_FILE_PATH = os.path.join(LOG_DIR, LOG_FILE)
# Configure logging
logging.basicConfig(
filename=LOG_FILE_PATH,
format="[ %(asctime)s ] %(lineno)d %(name)s - %(levelname)s - %(message)s",
level=logging.INFO,
)
# Add console handler for logging to console as well
console_handler = logging.StreamHandler()
console_handler.setLevel(logging.INFO)
formatter = logging.Formatter("[ %(asctime)s ] %(lineno)d %(name)s - %(levelname)s - %(message)s")
console_handler.setFormatter(formatter)
logging.getLogger().addHandler(console_handler)4. Exception Module
For custom exception handling:
src/exception/exception_handler.py
import sys
from src.utils.logger import logging
def error_message_detail(error, error_detail: sys):
“””
Create detailed error message with file and line information.
Args:
error: The error/exception object
error_detail: Error details from sys.exc_info()
Returns:
str: Formatted error message
"""
_, _, exc_tb = error_detail.exc_info()
file_name = exc_tb.tb_frame.f_code.co_filename
line_number = exc_tb.tb_lineno
error_message = f"Error occurred in Python script name [{file_name}] line number [{line_number}] error message [{str(error)}]"
return error_messageclass CustomException(Exception):
“””Custom exception class with detailed error message.”””
def __init__(self, error_message, error_detail: sys):
"""
Initialize custom exception.
Args:
error_message: Error message or exception
error_detail: Error details, typically sys module
"""
super().__init__(error_message)
self.error_message = error_message_detail(
error_message, error_detail=error_detail
)
def __str__(self):
"""
String representation of the exception.
Returns:
str: Error message
"""
return self.error_message5. Entity Module
For defining data structures and configurations:
# src/entity/config_entity.py
from dataclasses import dataclass
import os
@dataclass
class DataIngestionConfig:
"""Configuration for data ingestion."""
raw_data_path: str = os.path.join('artifacts', 'raw.csv')
train_data_path: str = os.path.join('artifacts', 'train.csv')
test_data_path: str = os.path.join('artifacts', 'test.csv')
@dataclass
class DataValidationConfig:
"""Configuration for data validation."""
schema_file_path: str = os.path.join('config', 'schema.json')
validation_report_path: str = os.path.join('artifacts', 'validation_report.json')
@dataclass
class DataTransformationConfig:
"""Configuration for data transformation."""
preprocessor_path: str = os.path.join('artifacts', 'preprocessor.pkl')
transformed_train_path: str = os.path.join('artifacts', 'transformed_train.npz')
transformed_test_path: str = os.path.join('artifacts', 'transformed_test.npz')
@dataclass
class ModelTrainerConfig:
"""Configuration for model trainer."""
trained_model_path: str = os.path.join('artifacts', 'model.pkl')
model_report_path: str = os.path.join('artifacts', 'model_report.json')
@dataclass
class ModelEvaluationConfig:
"""Configuration for model evaluation."""
evaluation_report_path: str = os.path.join('artifacts', 'evaluation_report.json')
@dataclass
class ModelDeploymentConfig:
"""Configuration for model deployment."""
model_deployment_path: str = os.path.join('artifacts', 'deployment')
# Add more deployment-specific configurations if neededArtifact Entity
# src/entity/artifact_entity.py
from dataclasses import dataclass
@dataclass
class DataIngestionArtifact:
"""Artifact produced by data ingestion component."""
train_file_path: str
test_file_path: str
@dataclass
class DataValidationArtifact:
"""Artifact produced by data validation component."""
validation_status: bool
validation_report_path: str
schema_file_path: str
@dataclass
class DataTransformationArtifact:
"""Artifact produced by data transformation component."""
transformed_train_path: str
transformed_test_path: str
preprocessor_path: str
@dataclass
class ModelTrainerArtifact:
"""Artifact produced by model trainer component."""
model_path: str
model_score: float
@dataclass
class ModelEvaluationArtifact:
"""Artifact produced by model evaluation component."""
is_model_accepted: bool
evaluation_report_path: str
@dataclass
class ModelDeploymentArtifact:
"""Artifact produced by model deployment component."""
deployment_status: bool
deployed_model_path: str
# Add more deployment artifacts if neededSetting Up the Project
Now let’s create the essential files for package setup and installation.
setup.py
This file is crucial for making your module installable and distributable:
from setuptools import find_packages, setup
from typing import List
# Declaring variables for setup functions
PROJECT_NAME = "ml-modular-project"
VERSION = "0.0.1"
AUTHOR = "Your Name"
DESCRIPTION = "A modular machine learning project"
REQUIREMENT_FILE_NAME = "requirements.txt"
def get_requirements_list() -> List[str]:
"""
This function returns a list of requirements from the requirements.txt file.
Returns:
List[str]: List of required packages
"""
with open(REQUIREMENT_FILE_NAME) as requirement_file:
return requirement_file.readlines().remove("-e .")
setup(
name=PROJECT_NAME,
version=VERSION,
author=AUTHOR,
description=DESCRIPTION,
packages=find_packages(),
install_requires=get_requirements_list()
)requirements.txt
List of all dependencies needed for the project:
pandas==2.0.3
numpy==1.24.3
scikit-learn==1.3.0
xgboost==1.7.6
matplotlib==3.7.2
seaborn==0.12.2
dill==0.3.7
fastapi==0.104.0
uvicorn==0.23.2
python-multipart==0.0.6
PyYAML==6.0.1
pytest==7.4.0
-e .main.py
The entry point for your application:
# main.py
import sys
from src.exception.exception_handler import CustomException
from src.utils.logger import logging
from src.pipeline.training_pipeline import TrainingPipeline
from src.pipeline.prediction_pipeline import PredictionPipeline, CustomData
def start_training():
"""Start the training pipeline."""
try:
logging.info("Starting training process")
# Initialize training pipeline
pipeline = TrainingPipeline()
# Example configurations
source_url = None # Optional URL to download data from
target_column = "target" # Target column name
target_column_index = -1 # Target column index in the numpy array
# Run the pipeline
results = pipeline.run_pipeline(
source_url=source_url,
target_column=target_column,
target_column_index=target_column_index
)
logging.info(f"Training completed with results: {results}")
return results
except Exception as e:
logging.error("Error in training")
raise CustomException(e, sys)
def start_prediction(data, model_path=None, preprocessor_path=None):
"""
Make predictions on input data.
Args:
data (dict): Input feature values
model_path (str, optional): Path to model
preprocessor_path (str, optional): Path to preprocessor
Returns:
Any: Prediction result
"""
try:
logging.info("Starting prediction process")
# Convert input data to DataFrame
custom_data = CustomData(**data)
features_df = custom_data.get_data_as_dataframe()
# Initialize prediction pipeline
prediction_pipeline = PredictionPipeline(
model_path=model_path,
preprocessor_path=preprocessor_path
)
# Make prediction
predictions = prediction_pipeline.predict(features_df)
logging.info(f"Prediction completed: {predictions}")
return predictions[0]
except Exception as e:
logging.error("Error in prediction")
raise CustomException(e, sys)
if __name__ == "__main__":
# Example: Run training
training_results = start_training()
# Example: Make prediction
sample_data = {
"feature1": 10,
"feature2": 20,
"feature3": "category_a"
}
prediction = start_prediction(
data=sample_data,
model_path=training_results["model_path"],
preprocessor_path=training_results["preprocessor_path"]
)
print(f"Prediction result: {prediction}")Automatic Setup
To automate the setup of components, we can create a script that generates the project structure:
# project_setup.py
import os
import sys
import shutil
def create_directory_structure():
"""Create the project directory structure."""
directories = [
"artifacts",
"config",
"logs",
"notebooks",
"src",
"src/components",
"src/pipeline",
"src/utils",
"src/exception",
"src/entity",
"tests",
"tests/unit",
"tests/integration"
]
for directory in directories:
os.makedirs(directory, exist_ok=True)
# Create __init__.py in Python module directories
if "src" in directory or "tests" in directory:
with open(os.path.join(directory, "__init__.py"), 'w') as f:
pass
print("Directory structure created successfully.")
def create_config_files():
"""Create configuration files."""
# Create schema.json
schema_json = {
"feature1": {"type": "numerical", "range": [0, 100]},
"feature2": {"type": "numerical", "range": [0, 500]},
"feature3": {"type": "categorical", "categories": ["category_a", "category_b", "category_c"]}
}
import json
with open(os.path.join("config", "schema.json"), 'w') as f:
json.dump(schema_json, f, indent=4)
# Create config.yaml
config_yaml = """
data_ingestion:
source_url: null
raw_data_path: artifacts/raw.csv
train_data_path: artifacts/train.csv
test_data_path: artifacts/test.csv
data_validation:
schema_file_path: config/schema.json
validation_report_path: artifacts/validation_report.json
data_transformation:
preprocessor_path: artifacts/preprocessor.pkl
transformed_train_path: artifacts/transformed_train.npz
transformed_test_path: artifacts/transformed_test.npz
model_trainer:
trained_model_path: artifacts/model.pkl
model_report_path: artifacts/model_report.json
model_evaluation:
evaluation_report_path: artifacts/evaluation_report.json
"""
with open(os.path.join("config", "config.yaml"), 'w') as f:
f.write(config_yaml)
print("Configuration files created successfully.")
def create_template_files():
"""Create template files for components."""
components = [
"data_ingestion",
"data_validation",
"data_transformation",
"model_trainer",
"model_evaluation",
"model_deployment"
]
# Template content
template = """# src/components/{component}.py
import os
import sys
from dataclasses import dataclass
from src.exception.exception_handler import CustomException
from src.utils.logger import logging
@dataclass
class {class_name}Config:
\"\"\"Configuration for {component_title}.\"\"\"
# Add configuration parameters here
pass
class {class_name}:
\"\"\"Class for {component_title} operations.\"\"\"
def __init__(self, config: {class_name}Config = {class_name}Config()):
\"\"\"Initialize {component_title} with configuration.\"\"\"
self.config = config
def initiate_{component}(self):
\"\"\"
Orchestrate the {component_title} process.
Returns:
Any: Result of {component_title}
\"\"\"
try:
logging.info("Initiating {component_title}")
# Implementation here
logging.info("{component_title} completed")
return "Success"
except Exception as e:
logging.error("Error in {component_title}")
raise CustomException(e, sys)
"""
for component in components:
class_name = "".join(word.capitalize() for word in component.split("_"))
component_title = " ".join(word for word in component.split("_"))
file_content = template.format(
component=component,
class_name=class_name,
component_title=component_title
)
with open(os.path.join("src", "components", f"{component}.py"), 'w') as f:
f.write(file_content)
# Create pipeline templates
pipeline_template = """# src/pipeline/{pipeline}.py
import os
import sys
from src.exception.exception_handler import CustomException
from src.utils.logger import logging
class {class_name}:
\"\"\"Class to orchestrate the {pipeline_title} pipeline.\"\"\"
def __init__(self):
\"\"\"Initialize the {pipeline_title} pipeline.\"\"\"
pass
def run_pipeline(self):
\"\"\"
Run the complete {pipeline_title} pipeline.
Returns:
dict: Pipeline results
\"\"\"
try:
logging.info("Starting {pipeline_title} pipeline")
# Implementation here
logging.info("{pipeline_title} pipeline completed successfully")
return {"status": "success"}
except Exception as e:
logging.error("Error in {pipeline_title} pipeline")
raise CustomException(e, sys)
"""
pipelines = [
"training_pipeline",
"prediction_pipeline"
]
for pipeline in pipelines:
class_name = "".join(word.capitalize() for word in pipeline.split("_"))
pipeline_title = " ".join(word for word in pipeline.split("_"))
file_content = pipeline_template.format(
pipeline=pipeline,
class_name=class_name,
pipeline_title=pipeline_title
)
with open(os.path.join("src", "pipeline", f"{pipeline}.py"), 'w') as f:
f.write(file_content)
# project_setup.py (continued)
# Create utility templates
utils = ["common", "logger"]
utils_template = """# src/utils/{util}.py
import os
import sys
from src.exception.exception_handler import CustomException
def sample_function():
\"\"\"Sample utility function.\"\"\"
try:
return "Success"
except Exception as e:
raise CustomException(e, sys)
"""
for util in utils:
with open(os.path.join("src", "utils", f"{util}.py"), 'w') as f:
f.write(utils_template.format(util=util))
# Create exception handler template
exception_template = """# src/exception/exception_handler.py
import sys
def error_message_detail(error, error_detail: sys):
\"\"\"
Create detailed error message with file and line information.
Args:
error: The error/exception object
error_detail: Error details from sys.exc_info()
Returns:
str: Formatted error message
\"\"\"
_, _, exc_tb = error_detail.exc_info()
file_name = exc_tb.tb_frame.f_code.co_filename
line_number = exc_tb.tb_lineno
error_message = f"Error occurred in Python script name [{file_name}] line number [{line_number}] error message [{str(error)}]"
return error_message
class CustomException(Exception):
\"\"\"Custom exception class with detailed error message.\"\"\"
def __init__(self, error_message, error_detail: sys):
\"\"\"
Initialize custom exception.
Args:
error_message: Error message or exception
error_detail: Error details, typically sys module
\"\"\"
super().__init__(error_message)
self.error_message = error_message_detail(
error_message, error_detail=error_detail
)
def __str__(self):
\"\"\"
String representation of the exception.
Returns:
str: Error message
\"\"\"
return self.error_message
"""
with open(os.path.join("src", "exception", "exception_handler.py"), 'w') as f:
f.write(exception_template)
# Create entity template files
entity_files = ["config_entity", "artifact_entity"]
entity_template = """# src/entity/{entity}.py
from dataclasses import dataclass
@dataclass
class SampleConfig:
\"\"\"Sample configuration class.\"\"\"
param1: str = "default_value"
param2: int = 10
"""
for entity in entity_files:
with open(os.path.join("src", "entity", f"{entity}.py"), 'w') as f:
f.write(entity_template.format(entity=entity))
print("Template files created successfully.")
def create_main_file():
"""Create main.py file."""
main_template = """# main.py
import sys
from src.exception.exception_handler import CustomException
from src.utils.logger import logging
from src.pipeline.training_pipeline import TrainingPipeline
from src.pipeline.prediction_pipeline import PredictionPipeline
def start_training():
\"\"\"Start the training pipeline.\"\"\"
try:
logging.info("Starting training process")
# Initialize training pipeline
pipeline = TrainingPipeline()
# Run the pipeline
results = pipeline.run_pipeline()
logging.info(f"Training completed with results: {results}")
return results
except Exception as e:
logging.error("Error in training")
raise CustomException(e, sys)
def start_prediction(data):
\"\"\"
Make predictions on input data.
Args:
data (dict): Input feature values
Returns:
Any: Prediction result
\"\"\"
try:
logging.info("Starting prediction process")
# Initialize prediction pipeline
prediction_pipeline = PredictionPipeline()
# Make prediction
predictions = prediction_pipeline.run_pipeline(data)
logging.info(f"Prediction completed: {predictions}")
return predictions
except Exception as e:
logging.error("Error in prediction")
raise CustomException(e, sys)
if __name__ == "__main__":
# Example: Run training
training_results = start_training()
# Example: Make prediction
sample_data = {
"feature1": 10,
"feature2": 20,
"feature3": "category_a"
}
prediction = start_prediction(sample_data)
print(f"Prediction result: {prediction}")
"""
with open("main.py", 'w') as f:
f.write(main_template)
print("Main file created successfully.")
def create_setup_files():
"""Create setup files for the package."""
setup_py = """from setuptools import find_packages, setup
from typing import List
# Declaring variables for setup functions
PROJECT_NAME = "ml-modular-project"
VERSION = "0.0.1"
AUTHOR = "Your Name"
DESCRIPTION = "A modular machine learning project"
REQUIREMENT_FILE_NAME = "requirements.txt"
def get_requirements_list() -> List[str]:
\"\"\"
This function returns a list of requirements from the requirements.txt file.
Returns:
List[str]: List of required packages
\"\"\"
with open(REQUIREMENT_FILE_NAME) as requirement_file:
requirements = requirement_file.readlines()
if "-e ." in requirements:
requirements.remove("-e .")
return [req.strip() for req in requirements]
setup(
name=PROJECT_NAME,
version=VERSION,
author=AUTHOR,
description=DESCRIPTION,
packages=find_packages(),
install_requires=get_requirements_list()
)
"""
with open("setup.py", 'w') as f:
f.write(setup_py)
requirements_txt = """pandas>=1.3.0
numpy>=1.20.0
scikit-learn>=1.0.0
xgboost>=1.5.0
matplotlib>=3.4.0
seaborn>=0.11.0
dill>=0.3.0
fastapi>=0.70.0
uvicorn>=0.15.0
python-multipart>=0.0.5
PyYAML>=6.0
pytest>=6.2.5
-e .
"""
with open("requirements.txt", 'w') as f:
f.write(requirements_txt)
# Create README.md
readme_md = """# Modular Machine Learning Project
A template for creating modular machine learning projects with best practices.
## Project Structure
```
ml-modular-project/
├── artifacts/ # Stores generated artifacts during pipeline execution
├── config/ # Configuration files
├── logs/ # Log files
├── notebooks/ # Jupyter notebooks for exploration
├── src/ # Source code
│ ├── components/ # Pipeline components
│ ├── entity/ # Data structures and configuration entities
│ ├── exception/ # Custom exception handling
│ ├── pipeline/ # Pipeline orchestration
│ └── utils/ # Utility functions
├── tests/ # Test cases
├── main.py # Entry point
├── requirements.txt # Project dependencies
└── setup.py # Package setup file
```
## Installation
```bash
pip install -r requirements.txt
```
## Usage
### Training
```python
from main import start_training
results = start_training()
```
### Prediction
```python
from main import start_prediction
data = {
"feature1": 10,
"feature2": 20,
"feature3": "category_a"
}
prediction = start_prediction(data)
```
"""
with open("README.md", 'w') as f:
f.write(readme_md)
print("Setup files created successfully.")
def create_test_files():
"""Create template test files."""
unit_test_template = """# tests/unit/test_{component}.py
import unittest
import os
import sys
import shutil
from src.components.{component} import {class_name}
class Test{class_name}(unittest.TestCase):
\"\"\"Unit tests for {class_name} component.\"\"\"
def setUp(self):
\"\"\"Set up test environment.\"\"\"
# Setup code here
pass
def tearDown(self):
\"\"\"Clean up test environment.\"\"\"
# Cleanup code here
pass
def test_initiate_{component}(self):
\"\"\"Test initiate_{component} method.\"\"\"
# Test implementation here
self.assertTrue(True)
if __name__ == "__main__":
unittest.main()
"""
components = [
"data_ingestion",
"data_validation",
"data_transformation",
"model_trainer",
"model_evaluation"
]
for component in components:
class_name = "".join(word.capitalize() for word in component.split("_"))
with open(os.path.join("tests", "unit", f"test_{component}.py"), 'w') as f:
f.write(unit_test_template.format(component=component, class_name=class_name))
# Create integration test template
integration_test_template = """# tests/integration/test_pipeline.py
import unittest
import os
import sys
import shutil
from src.pipeline.training_pipeline import TrainingPipeline
from src.pipeline.prediction_pipeline import PredictionPipeline
class TestPipelines(unittest.TestCase):
\"\"\"Integration tests for pipelines.\"\"\"
def setUp(self):
\"\"\"Set up test environment.\"\"\"
# Setup code here
pass
def tearDown(self):
\"\"\"Clean up test environment.\"\"\"
# Cleanup code here
pass
def test_training_pipeline(self):
\"\"\"Test training pipeline.\"\"\"
# Test implementation here
self.assertTrue(True)
def test_prediction_pipeline(self):
\"\"\"Test prediction pipeline.\"\"\"
# Test implementation here
self.assertTrue(True)
if __name__ == "__main__":
unittest.main()
"""
with open(os.path.join("tests", "integration", "test_pipeline.py"), 'w') as f:
f.write(integration_test_template)
print("Test files created successfully.")
def main():
"""Main function to orchestrate project setup."""
try:
print("Starting project setup...")
create_directory_structure()
create_config_files()
create_template_files()
create_main_file()
create_setup_files()
create_test_files()
print("\nProject setup completed successfully!")
print("\nTo get started:")
print("1. Install requirements: pip install -r requirements.txt")
print("2. Run the project: python main.py")
except Exception as e:
print(f"Error in project setup: {e}")
sys.exit(1)
if __name__ == "__main__":
main()Building Production-Ready ML Projects: A Modular Approach
Building Production-Ready ML Projects: A Modular Approach
In the fast-evolving landscape of machine learning applications, developing production-ready projects demands more than just model building. It requires a systematic approach with proper organization, error handling, logging, and a modular architecture. This blog post introduces a comprehensive framework for creating modular machine learning projects that are robust, maintainable, and ready for production deployment.
Why Modular Architecture Matters in ML Projects
Machine learning projects often begin as exploratory notebooks but rapidly grow complex when transitioning to production. A modular architecture addresses several challenges:
- Maintainability: Isolating components makes code easier to maintain and update
- Reusability: Well-defined modules can be reused across different projects
- Testability: Independent components are easier to test thoroughly
- Collaboration: Clear boundaries enable teams to work on different components simultaneously
- Deployment: Modular systems are easier to deploy and scale in production environments
Project Structure
Our modular ML project template follows this structure:
ml-modular-project/
├── artifacts/ # Stores generated artifacts during pipeline execution
├── config/ # Configuration files
├── logs/ # Log files
├── notebooks/ # Jupyter notebooks for exploration
├── src/ # Source code
│ ├── components/ # Pipeline components
│ ├── entity/ # Data structures and configuration entities
│ ├── exception/ # Custom exception handling
│ ├── pipeline/ # Pipeline orchestration
│ └── utils/ # Utility functions
├── tests/ # Test cases
├── main.py # Entry point
├── requirements.txt # Project dependencies
└── setup.py # Package setup file
Core Components
1. Data Ingestion
The data ingestion component handles importing data from various sources (databases, CSV files, APIs) and splitting it into training and testing datasets. Its key responsibilities include:
- Downloading data from specified sources
- Reading data into appropriate formats
- Performing initial cleaning if necessary
- Splitting data into training and testing sets
- Saving processed datasets
2. Data Validation
Data validation ensures that incoming data meets expected quality standards before proceeding to model training. This component:
- Validates schema conformance (column names, data types)
- Checks for missing values and outliers
- Verifies data distributions
- Generates validation reports
- Raises alerts when data quality issues arise
3. Data Transformation
The transformation component prepares data for machine learning algorithms by:
- Handling missing values
- Encoding categorical variables
- Scaling numerical features
- Creating feature pipelines
- Generating new features
- Saving transformation artifacts for prediction
4. Model Trainer
This component handles the machine learning model development:
- Training different model algorithms
- Tuning hyperparameters
- Evaluating model performance
- Saving trained models
- Generating training reports
5. Model Evaluation
The evaluation component assesses model performance against production or baseline models:
- Comparing metrics with existing models
- Determining if a new model is better than the current one
- Creating detailed evaluation reports
- Deciding whether to accept or reject new models
Pipeline Orchestration
Two main pipelines orchestrate the flow of data and operations:
Training Pipeline
The training pipeline coordinates the end-to-end model development process:
class TrainingPipeline:
def run_pipeline(self, source_url=None, target_column=None, target_column_index=-1):
# Data Ingestion
train_data_path, test_data_path = self.start_data_ingestion(source_url)
# Data Validation
validation_status = self.start_data_validation(train_data_path, test_data_path)
# Data Transformation
transformed_train_path, transformed_test_path, preprocessor_path = self.start_data_transformation(
train_data_path, test_data_path, target_column
)
# Model Training
model_path = self.start_model_training(
transformed_train_path, transformed_test_path, target_column_index
)
# Model Evaluation
evaluation_report = self.start_model_evaluation(
transformed_test_path, model_path, preprocessor_path, target_column_index
)
return {
"model_path": model_path,
"preprocessor_path": preprocessor_path,
"evaluation_report": evaluation_report
}
Prediction Pipeline
The prediction pipeline handles making predictions using trained models:
class PredictionPipeline:
def predict(self, features: pd.DataFrame) -> np.ndarray:
# Load model and preprocessor
preprocessor = load_object(file_path=self.preprocessor_path)
model = load_object(file_path=self.model_path)
# Transform features
transformed_features = preprocessor.transform(features)
# Make predictions
predictions = model.predict(transformed_features)
return predictions
Utilities and Support Features
Custom Exception Handling
A robust error handling system improves debugging and troubleshooting:
class CustomException(Exception):
def __init__(self, error_message, error_detail: sys):
super().__init__(error_message)
self.error_message = error_message_detail(
error_message, error_detail=error_detail
)
def __str__(self):
return self.error_message
Logging System
Comprehensive logging provides insights into system operations:
logging.basicConfig(
filename=LOG_FILE_PATH,
format="[ %(asctime)s ] %(lineno)d %(name)s - %(levelname)s - %(message)s",
level=logging.INFO,
)
Entity Configurations
Data classes define configurations and artifacts for each component:
@dataclass
class DataIngestionConfig:
raw_data_path: str = os.path.join('artifacts', 'raw.csv')
train_data_path: str = os.path.join('artifacts', 'train.csv')
test_data_path: str = os.path.join('artifacts', 'test.csv')
Testing Strategy
A comprehensive testing strategy includes:
- Unit Tests: Testing individual components in isolation
- Integration Tests: Testing interactions between components
- End-to-End Tests: Testing complete pipelines
Using the Template
- Setting Up the Project Run the project setup script to create the directory structure and template files:
python project_setup.py - Installing Dependencies
pip install -r requirements.txt - Implementing Components Fill in the implementation details for each component based on your specific use case.
- Running the Pipeline
from main import start_training, start_prediction # Train model training_results = start_training() # Make prediction data = {"feature1": 10, "feature2": 20, "feature3": "category_a"} prediction = start_prediction(data)
Best Practices
- Configuration Management: Store all configurable parameters in configuration files
- Artifact Management: Save intermediate artifacts for reproducibility and debugging
- Exception Handling: Use custom exceptions for clear error messages
- Logging: Implement comprehensive logging for monitoring and debugging
- Testing: Create tests for all components to ensure reliability
- Documentation: Document code thoroughly for maintainability
Conclusion
Building a modular machine learning project requires careful planning and structure, but the benefits far outweigh the initial investment. This architecture provides a solid foundation for developing ML systems that are maintainable, scalable, and production-ready.
By following the patterns outlined in this post, you can streamline your ML development workflow and focus on solving business problems rather than wrestling with code organization issues.
Whether you’re working on a small personal project or a large enterprise system, this modular approach will help you create robust machine learning applications that can confidently transition from experimentation to production.
Air Quality Index Monitoring webpage using Google maps API using Python
In an era where environmental concerns increasingly shape public policy and personal health decisions, access to real-time air quality data has never been more crucial. The AQI Google Maps project represents an innovative approach to environmental monitoring, combining Google Maps’ familiar interface with critical air quality metrics. This open-source initiative transforms complex environmental data into an accessible visualization tool that can benefit researchers, policymakers, and everyday citizens concerned about the air they breathe.
What is the AQI Google Maps Project?
The AQI (Air Quality Index) Google Maps project is an open-source web application that integrates air quality data with Google Maps to provide a visual representation of air pollution levels across different locations. Developed by Tejas K (GitHub: tejask0512), this project leverages modern web technologies and public APIs to create an interactive map where users can view air quality conditions with intuitive color-coded markers.
Technical Architecture
The project employs a straightforward yet effective technical stack:
- Frontend: HTML, CSS, JavaScript
- APIs: Google Maps API for mapping functionality, Air Quality APIs for pollution data
- Data Visualization: Custom markers and color-coding system
The core functionality revolves around fetching air quality data based on geographic coordinates and rendering this information as color-coded markers on the Google Maps interface. The colors transition from green (good air quality) through yellow and orange to red and purple (hazardous air quality), providing an immediate visual understanding of conditions in different areas.
Deep Dive into AQI Analysis
Understanding the Air Quality Index
The Air Quality Index is a standardized indicator developed by environmental agencies to communicate how polluted the air is and what associated health effects might be. The AQI Google Maps project implements this complex calculation system and presents it in an accessible format.
The AQI typically accounts for multiple pollutants:
| Pollutant | Source | Health Impact |
|---|---|---|
| PM2.5 (Fine Particulate Matter) | Combustion engines, forest fires, industrial processes | Can penetrate deep into lungs and bloodstream |
| PM10 (Coarse Particulate Matter) | Dust, pollen, mold | Respiratory irritation, asthma exacerbation |
| O3 (Ozone) | Created by chemical reactions between NOx and VOCs | Lung damage, respiratory issues |
| NO2 (Nitrogen Dioxide) | Vehicles, power plants | Respiratory inflammation |
| SO2 (Sulfur Dioxide) | Fossil fuel combustion, industrial processes | Respiratory issues, contributes to acid rain |
| CO (Carbon Monoxide) | Incomplete combustion | Reduces oxygen delivery in bloodstream |
The project likely calculates an overall AQI based on the highest concentration of any single pollutant, following the EPA’s approach where:
- 0-50 (Green): Good air quality with minimal health concerns
- 51-100 (Yellow): Moderate air quality; unusually sensitive individuals may experience issues
- 101-150 (Orange): Unhealthy for sensitive groups
- 151-200 (Red): Unhealthy for all groups
- 201-300 (Purple): Very unhealthy; may trigger health alerts
- 301+ (Maroon): Hazardous; serious health effects for entire population
The technical implementation likely includes conversion formulas to normalize different pollutant measurements to the same 0-500 AQI scale.
Real-time Data Processing
A key technical achievement of the project is its ability to process real-time air quality data. This involves:
- API Integration: Connecting to air quality data providers through RESTful APIs
- Data Parsing: Extracting relevant metrics from JSON/XML responses
- Coordinate Mapping: Associating pollution data with precise geographic coordinates
- Temporal Synchronization: Managing data freshness and update frequencies
The project handles these operations seamlessly in the background, presenting users with up-to-date information without exposing the complexity of the underlying data acquisition process.
Report Generation Capabilities
One of the project’s valuable features is its ability to generate comprehensive air quality reports. These reports serve multiple purposes:
Types of Reports Generated
- Location-specific Snapshots: Detailed breakdowns of current air quality at selected points
- Comparative Analysis: Contrasting air quality across multiple locations
- Temporal Reports: Tracking air quality changes over time (hourly, daily, weekly)
- Pollutant-specific Reports: Focusing on individual contaminants like PM2.5 or O3
Report Components
The reporting system likely includes:
- Statistical Summaries: Min/max/mean values for AQI metrics
- Health Impact Assessments: Explanations of potential health effects based on current readings
- Visualizations: Charts and graphs depicting pollution trends
- Contextual Information: Weather conditions that may influence readings
- Actionable Recommendations: Suggested activities based on air quality levels
Technical Implementation of Reporting
From a development perspective, the reporting functionality demonstrates sophisticated data processing:
// Conceptual example of report generation logic
function generateAQIReport(locationData, timeframe) {
const reportData = {
location: locationData.name,
coordinates: locationData.coordinates,
timestamp: new Date(),
metrics: {
overall: calculateOverallAQI(locationData.pollutants),
individual: locationData.pollutants,
trends: analyzeTrends(locationData.history, timeframe)
},
healthImplications: assessHealthImpact(calculateOverallAQI(locationData.pollutants)),
recommendations: generateRecommendations(calculateOverallAQI(locationData.pollutants))
};
return formatReport(reportData, preferredFormat);
}
This functionality transforms raw data into actionable intelligence, making the project valuable beyond simple visualization.
AQI and Location Coordinate Data for Machine Learning
Perhaps the most forward-looking aspect of the project is its potential for generating valuable datasets for machine learning applications. The combination of precise geolocation data with corresponding air quality metrics creates numerous possibilities for advanced environmental analysis.
Data Generation for ML Models
The project effectively creates a continuous stream of structured data points with these key attributes:
- Geographic Coordinates: Latitude and longitude
- Temporal Information: Timestamps for each measurement
- Multiple Pollutant Metrics: PM2.5, PM10, O3, NO2, SO2, CO values
- Calculated AQI: Overall air quality index
- Contextual Metadata: Potentially including weather conditions, urban density, etc.
This multi-dimensional dataset serves as excellent training data for various machine learning models.
Potential ML Applications
With sufficient data collection over time, the following machine learning approaches become possible:
1. Predictive Modeling
Machine learning algorithms can be trained to forecast air quality based on historical patterns:
- Time Series Forecasting: Using techniques like ARIMA, LSTM networks, or Prophet to predict AQI values hours or days in advance
- Multivariate Prediction: Incorporating weather forecasts, traffic patterns, and seasonal factors to improve accuracy
- Anomaly Detection: Identifying unusual pollution events that deviate from expected patterns
# Conceptual example of LSTM model for AQI prediction
from keras.models import Sequential
from keras.layers import LSTM, Dense
def build_aqi_prediction_model(lookback_window):
model = Sequential()
model.add(LSTM(50, activation='relu', input_shape=(lookback_window, n_features)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')
return model
# Train with historical AQI data from project
model = build_aqi_prediction_model(24) # 24-hour lookback window
model.fit(X_train, y_train, epochs=100, validation_split=0.2)
2. Spatial Analysis and Interpolation
The geospatial nature of the data enables sophisticated spatial modeling:
- Kriging/Gaussian Process Regression: Estimating pollution levels between measurement points
- Spatial Autocorrelation: Analyzing how pollution levels at one location influence nearby areas
- Hotspot Identification: Using clustering algorithms to detect persistent pollution sources
# Conceptual example of spatial interpolation
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel
def interpolate_aqi_surface(known_points, known_values, grid_points):
# Define kernel - distance matters for pollution spread
kernel = RBF(length_scale=1.0) + WhiteKernel(noise_level=0.1)
gpr = GaussianProcessRegressor(kernel=kernel)
# Train on known AQI points
gpr.fit(known_points, known_values)
# Predict AQI at all grid points
predicted_values = gpr.predict(grid_points)
return predicted_values
3. Causal Analysis
Advanced machine learning techniques can help identify pollution drivers:
- Causal Inference Models: Determining the impact of traffic changes, industrial activities, or policy interventions on air quality
- Counterfactual Analysis: Estimating what air quality would be under different conditions
- Attribution Modeling: Quantifying the contribution of different sources to overall pollution levels
4. Computer Vision Integration
The project’s map-based approach opens possibilities for combining with visual data:
- Satellite Imagery Analysis: Correlating visible pollution (smog, industrial activity) with measured AQI
- Traffic Density Estimation: Using traffic camera feeds to predict localized pollution spikes
- Urban Development Impact: Analyzing how changes in urban landscapes affect air quality patterns
Implementation Considerations for ML Integration
To fully realize the machine learning potential, the project could implement:
- Data Export APIs: Programmatic access to historical AQI and coordinate data
- Standardized Dataset Generation: Creating properly formatted, cleaned datasets ready for ML models
- Feature Engineering Utilities: Tools to extract temporal patterns, spatial relationships, and other derived features
- Model Integration Endpoints: APIs that allow trained models to feed predictions back into the visualization system
// Conceptual implementation of data export for ML
function exportTrainingData(startDate, endDate, region, format='csv') {
const dataPoints = fetchHistoricalData(startDate, endDate, region);
// Process for ML readiness
const mlReadyData = dataPoints.map(point => ({
timestamp: point.timestamp,
lat: point.coordinates.lat,
lng: point.coordinates.lng,
pm25: point.pollutants.pm25,
pm10: point.pollutants.pm10,
o3: point.pollutants.o3,
no2: point.pollutants.no2,
so2: point.pollutants.so2,
co: point.pollutants.co,
aqi: point.aqi,
// Derived features
hour_of_day: new Date(point.timestamp).getHours(),
day_of_week: new Date(point.timestamp).getDay(),
is_weekend: [0, 6].includes(new Date(point.timestamp).getDay()),
season: calculateSeason(point.timestamp)
}));
return formatDataForExport(mlReadyData, format);
}
Key Features and Capabilities
The project demonstrates several notable features:
- Real-time air quality visualization: Displays current AQI values at selected locations
- Interactive map interface: Users can navigate, zoom, and click on markers to view detailed information
- Color-coded AQI indicators: Intuitive visual representation of pollution levels
- Customizable markers: Location-specific information about air quality conditions
- Responsive design: Functions across various device types and screen sizes
Environmental and Health Significance
The importance of this project extends far beyond its technical implementation. Here’s why such tools matter:
Public Health Impact
Air pollution is directly linked to numerous health problems, including respiratory diseases, cardiovascular issues, and even neurological disorders. According to the World Health Organization, air pollution causes approximately 7 million premature deaths annually worldwide. By making air quality data more accessible, this project empowers individuals to:
- Make informed decisions about outdoor activities
- Understand when to take protective measures (like wearing masks or staying indoors)
- Recognize patterns in local air quality that might affect their health
Environmental Awareness
Environmental literacy begins with awareness. When people can visually connect with environmental data, they’re more likely to:
- Understand the scope and severity of air pollution issues
- Recognize temporal and spatial patterns in air quality
- Connect human activities with environmental outcomes
- Support policies aimed at improving air quality
Research and Policy Applications
For researchers and policymakers, visualized air quality data offers valuable insights:
- Identifying pollution hotspots that require intervention
- Evaluating the effectiveness of environmental regulations
- Planning urban development with air quality considerations
- Allocating resources for environmental monitoring and mitigation
Case Study: Urban Planning and Environmental Justice
The AQI Google Maps project provides a powerful tool for addressing environmental justice concerns. By visualizing pollution patterns across different neighborhoods, it can reveal disparities in air quality that often correlate with socioeconomic factors.
Data-Driven Environmental Justice
Researchers can use the generated datasets to:
- Identify Disproportionate Impacts: Quantify differences in air quality across neighborhoods with varying income levels or racial demographics
- Temporal Justice Analysis: Determine if certain communities bear the burden of poor air quality during specific times (e.g., industrial activity hours)
- Policy Effectiveness: Measure how environmental regulations impact different communities
Practical Application Example
Consider a city planning department using the AQI Google Maps project to assess the impact of a proposed industrial development:
- Establish baseline air quality readings across all affected neighborhoods
- Use predictive modeling (with the ML techniques described above) to estimate pollution changes
- Generate reports showing projected AQI impacts on different communities
- Adjust development plans to minimize disproportionate impacts on vulnerable populations
This data-driven approach promotes equitable development and environmental protection.
The Future of Environmental Data Integration
The AQI Google Maps project represents an important step toward more integrated environmental monitoring. Future development could include:
Data Fusion Opportunities
- Cross-Pollutant Analysis: Investigating relationships between different pollutants
- Multi-Environmental Factor Integration: Combining air quality with noise pollution, water quality, and urban heat island effects
- Health Data Correlation: Connecting real-time AQI with emergency room visits for respiratory issues
Technical Evolution
- Edge Computing Integration: Processing air quality data from low-cost sensors at the edge
- Blockchain for Data Integrity: Ensuring the provenance and authenticity of environmental measurements
- Federated Learning: Enabling distributed model training across multiple air quality monitoring networks
Conclusion
The AQI Google Maps project represents an important intersection of environmental monitoring, data visualization, and public information. Its ability to generate structured air quality data associated with precise geographic coordinates creates a foundation for sophisticated analysis and machine learning applications.
By democratizing access to environmental data and creating opportunities for advanced computational analysis, this project contributes to both public awareness and scientific advancement. The potential for machine learning integration further elevates its significance, enabling predictive capabilities and deeper insights into pollution patterns.
As we continue to face environmental challenges, projects like this demonstrate how technology can be leveraged not just for convenience or entertainment, but for creating a more informed and environmentally conscious society. The combination of visual accessibility with data generation for machine learning represents a powerful approach to environmental monitoring that can drive both individual awareness and systemic change.
This blog post analyzes the AQI Google Maps project developed by Tejas Kamble {https://github.com/tejask0512/AQI-Google-Maps}. The project is open-source and available for contributions on GitHub.

Comprehensive Guide to NLP Text Representation Techniques
Natural Language Processing (NLP) requires converting human language into numerical formats that computers can understand. This guide explores major text representation techniques in depth, comparing their strengths, weaknesses, and practical applications.
1. One-Hot Encoding
One-hot encoding is a fundamental representation technique that forms the conceptual foundation for many text representation methods.
How It Works
One-hot encoding represents each word as a binary vector with a length equal to the vocabulary size. For a vocabulary of size V:
- Create a vector of length V filled with zeros
- Set the position corresponding to the word’s index to 1
- All other positions remain 0
Detailed Example
Consider a small vocabulary: [“apple”, “banana”, “cherry”, “date”, “elderberry”]
One-hot encodings:
- “apple” = [1, 0, 0, 0, 0]
- “banana” = [0, 1, 0, 0, 0]
- “cherry” = [0, 0, 1, 0, 0]
- “date” = [0, 0, 0, 1, 0]
- “elderberry” = [0, 0, 0, 0, 1]
To represent the sentence “I like apple and banana”:
- We would create five separate vectors for each word
- Words not in our vocabulary (like “I”, “like”, “and”) would either be ignored or added to the vocabulary
Mathematical Formulation
For a vocabulary V = {w₁, w₂, …, wₙ}, the one-hot encoding of word wᵢ is a vector v where:
- v[j] = 1 if j = i
- v[j] = 0 if j ≠ i
Advantages
- Simplicity: Straightforward to implement and understand
- Unique Representation: Each word has a distinct representation
- No Assumptions: Makes no assumptions about relationships between words
- Lossless: Preserves word identity perfectly
Disadvantages
- Dimensionality: For real vocabularies (50,000+ words), vectors become enormous
- Sparsity: Most elements are zero, wasting memory and computation
- No Semantic Information: “apple” and “fruit” are as different as “apple” and “rocket”
- No Contextual Information: The same word always has the same representation regardless of usage
Code Implementation
def one_hot_encode(word, vocabulary):
vector = [0] * len(vocabulary)
if word in vocabulary:
vector[vocabulary.index(word)] = 1
return vector
vocabulary = ["apple", "banana", "cherry", "date", "elderberry"]
print(one_hot_encode("banana", vocabulary)) # [0, 1, 0, 0, 0]
print(one_hot_encode("apple", vocabulary)) # [1, 0, 0, 0, 0]
2. Bag of Words (BoW)
Bag of Words builds on one-hot encoding to represent entire documents rather than individual words.
How It Works
- Create a vocabulary from all unique words in the corpus
- For each document:
- Initialize a vector of zeros with length equal to vocabulary size
- For each word in the document, increment the corresponding position
- The final vector contains counts of word occurrences
Detailed Example
Consider two documents:
- Document 1: “The cat sat on the mat”
- Document 2: “The dog chased the cat”
Vocabulary: [“the”, “cat”, “sat”, “on”, “mat”, “dog”, “chased”]
BoW representations:
- Document 1: [2, 1, 1, 1, 1, 0, 0] (2 occurrences of “the”, 1 of “cat”, etc.)
- Document 2: [2, 1, 0, 0, 0, 1, 1]
Mathematical Formulation
For a document D and vocabulary V = {w₁, w₂, …, wₙ}, the BoW representation is a vector v where:
- v[i] = count of word wᵢ in document D
Advantages
- Frequency Information: Captures how often words appear
- Document Comparison: Enables comparing documents based on content
- Simplicity: Easy to implement and understand
- Scalability: Works well with many classification algorithms
- Success in Practice: Despite simplicity, works well for many tasks like spam detection and document categorization
Disadvantages
- Loss of Order: “The cat chased the dog” and “The dog chased the cat” have identical representations
- Equal Weighting: Common words like “the” get high values despite low information content
- Sparse Representation: Most entries are zero for large vocabularies
- No Semantics: Doesn’t capture word relationships or meanings
Practical Applications
- Sentiment Analysis: Determining whether reviews are positive or negative
- Spam Detection: Identifying unwanted emails
- Document Categorization: Sorting documents into topics
Code Implementation
from collections import Counter
def create_bow(document, vocabulary):
word_counts = Counter(document.lower().split())
return [word_counts.get(word, 0) for word in vocabulary]
vocabulary = ["the", "cat", "sat", "on", "mat", "dog", "chased"]
doc1 = "The cat sat on the mat"
doc2 = "The dog chased the cat"
bow1 = create_bow(doc1, vocabulary)
bow2 = create_bow(doc2, vocabulary)
print(bow1) # [2, 1, 1, 1, 1, 0, 0]
print(bow2) # [2, 1, 0, 0, 0, 1, 1]
3. TF-IDF (Term Frequency-Inverse Document Frequency)
TF-IDF enhances BoW by weighting terms based on their importance within and across documents.
How It Works
TF-IDF consists of two components:
- Term Frequency (TF): Measures how frequently a term appears in a document
- TF(t,d) = (Number of times term t appears in document d) / (Total number of terms in document d)
- Inverse Document Frequency (IDF): Measures how important a term is across the corpus
- IDF(t) = log(Total number of documents / Number of documents containing term t)
The final TF-IDF score is: TF-IDF(t,d) = TF(t,d) × IDF(t)
Detailed Example
Consider a corpus of three documents:
- Doc1: “The cat sat on the mat”
- Doc2: “The dog chased the cat”
- Doc3: “The bird flew over the house”
Let’s calculate the TF-IDF for the word “cat” in Doc1:
- Term Frequency for “cat” in Doc1:
- TF(“cat”,Doc1) = 1/6 = 0.167
- Inverse Document Frequency for “cat”:
- “cat” appears in 2 out of 3 documents
- IDF(“cat”) = log(3/2) ≈ log(1.5) ≈ 0.176
- TF-IDF for “cat” in Doc1:
- TF-IDF(“cat”,Doc1) = 0.167 × 0.176 ≈ 0.029
Compare this with the common word “the”:
- TF(“the”, Doc1) = 2/6 = 0.333
- IDF(“the”) = log(3/3) = log(1) = 0
- TF-IDF(“the”,Doc1) = 0.333 × 0 = 0
This shows how TF-IDF reduces the weight of common words that appear in all documents.
Mathematical Formulation
For term t in document d, from a corpus D:
- TF(t,d) = f(t,d) / Σₓ f(x,d) where f(t,d) is the count of term t in document d
- IDF(t) = log(|D| / |{d ∈ D : t ∈ d}|) where |D| is the total number of documents
- TF-IDF(t,d) = TF(t,d) × IDF(t)
Advantages
- Word Importance: Distinguishes between common and distinctive terms
- Weighting Mechanism: Reduces the impact of high-frequency, low-information words
- Enhanced Discrimination: Highlights words that characterize specific documents
- Proven Effectiveness: Outperforms raw BoW in many tasks
- Interpretability: Values have clear meaning (higher = more distinctive)
Disadvantages
- Still Ignores Order: Word sequence is not considered
- Corpus Dependency: IDF calculation requires a complete corpus
- No Semantic Understanding: Doesn’t capture word relationships
- Fixed Vocabulary: Struggles with out-of-vocabulary words
- Limited Context: Doesn’t capture word usage context
Practical Applications
- Information Retrieval: Powering search engines
- Document Clustering: Grouping similar documents
- Feature Extraction: Creating input features for machine learning algorithms
- Keyword Extraction: Identifying the most distinctive words in text
Code Implementation
import numpy as np
from collections import Counter
from sklearn.feature_extraction.text import TfidfVectorizer
# Manual implementation
def compute_tfidf(corpus):
# Create vocabulary
all_words = set()
for doc in corpus:
for word in doc.lower().split():
all_words.add(word)
vocabulary = list(all_words)
# Calculate document frequency
doc_freq = Counter()
for doc in corpus:
words_in_doc = set(doc.lower().split())
for word in words_in_doc:
doc_freq[word] += 1
# Calculate TF-IDF
tfidf_vectors = []
for doc in corpus:
word_counts = Counter(doc.lower().split())
total_words = len(doc.lower().split())
tfidf_vector = []
for word in vocabulary:
# Term frequency
tf = word_counts.get(word, 0) / total_words
# Inverse document frequency
idf = np.log(len(corpus) / doc_freq.get(word, 1))
# TF-IDF
tfidf_vector.append(tf * idf)
tfidf_vectors.append(tfidf_vector)
return tfidf_vectors, vocabulary
# Example usage
corpus = [
"The cat sat on the mat",
"The dog chased the cat",
"The bird flew over the house"
]
tfidf_vectors, vocab = compute_tfidf(corpus)
print(f"Vocabulary: {vocab}")
print(f"TF-IDF for document 1: {tfidf_vectors[0]}")
# Using scikit-learn
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(corpus)
print("scikit-learn TF-IDF:")
print(X.toarray())
4. Word2Vec
Word2Vec represents a paradigm shift in text representation by generating dense, continuous vector embeddings that capture semantic relationships between words.
How It Works
Word2Vec uses shallow neural networks with two main architectures:
- Skip-gram:
- Input: Target word
- Output: Context words (surrounding words)
- The model learns to predict the context from a single word
- Continuous Bag of Words (CBOW):
- Input: Context words
- Output: Target word
- The model learns to predict a word from its context
During training, Word2Vec adjusts word vectors to maximize the probability of correct predictions, resulting in semantically similar words having similar embeddings.
Detailed Example
Consider training Word2Vec on this corpus: “The quick brown fox jumps over the lazy dog.”
For a window size of 2, training examples for Skip-gram include:
- Input: “quick”, Output: [“The”, “brown”, “fox”]
- Input: “brown”, Output: [“quick”, “fox”, “jumps”]
- Input: “fox”, Output: [“brown”, “quick”, “jumps”, “over”]
After training, similar words have similar vectors. For example, the vectors for “king”, “queen”, “man”, and “woman” would capture their semantic relationships, enabling vector arithmetic like:
- vec(“king”) – vec(“man”) + vec(“woman”) ≈ vec(“queen”)
Mathematical Formulation
For the Skip-gram model, the objective is to maximize:
- log P(context|word) = Σᵢ₌₁ᵀ Σⱼ∈context(i) log P(wⱼ|wᵢ)
Where P(wⱼ|wᵢ) is modeled using the softmax function:
- P(wⱼ|wᵢ) = exp(vᵀwⱼ · vwᵢ) / Σₖ₌₁ᵛ exp(vᵀwₖ · vwᵢ)
Where vwᵢ is the vector for the input word, and vᵀwⱼ is the vector for the context word.
Advantages
- Semantic Relationships: Captures word similarity and relationships
- Dense Representation: Low-dimensional vectors (typically 100-300 dimensions)
- Vector Arithmetic: Enables mathematical operations on word meanings
- Transferability: Pre-trained embeddings can be used across different tasks
- Performance: Dramatically improves results on many NLP tasks
Disadvantages
- Training Requirements: Needs large text corpora and computational resources
- Fixed Vocabulary: Cannot handle out-of-vocabulary words
- Single Representation: One vector per word, regardless of context
- No Polysemy: Cannot represent multiple meanings of the same word
- Black Box: Difficult to interpret individual dimensions
Practical Applications
- Semantic Similarity: Finding related words or documents
- Machine Translation: Improving language translation
- Named Entity Recognition: Identifying entities in text
- Text Classification: Enhancing document categorization
- Recommendation Systems: Finding similar items based on descriptions
Code Implementation
from gensim.models import Word2Vec
import numpy as np
# Sample corpus
sentences = [
["the", "quick", "brown", "fox", "jumps", "over", "the", "lazy", "dog"],
["the", "brown", "fox", "is", "quick", "and", "the", "dog", "is", "lazy"],
["quick", "brown", "foxes", "jump", "over", "lazy", "dogs"]
]
# Train model
model = Word2Vec(sentences, vector_size=100, window=5, min_count=1, workers=4)
# Explore word vectors
print(f"Vector for 'fox': {model.wv['fox'][:5]}...") # Show first 5 dimensions
# Find similar words
similar_words = model.wv.most_similar("fox", topn=3)
print(f"Words similar to 'fox': {similar_words}")
# Vector arithmetic
result = model.wv.most_similar(positive=["quick", "dog"], negative=["lazy"], topn=1)
print(f"quick - lazy + dog: {result}")
# Manual similarity calculation
cosine_similarity = np.dot(model.wv["fox"], model.wv["dog"]) / (
np.linalg.norm(model.wv["fox"]) * np.linalg.norm(model.wv["dog"])
)
print(f"Cosine similarity between 'fox' and 'dog': {cosine_similarity}")
5. GloVe (Global Vectors for Word Representation)
GloVe combines the benefits of matrix factorization methods and local context window methods.
How It Works
- Build a co-occurrence matrix X, where Xᵢⱼ represents how often word i appears in the context of word j
- Define a weighting function f(Xᵢⱼ) that gives less weight to rare and extremely common co-occurrences
- Find word vectors wᵢ and context vectors w̃ⱼ such that their dot product approximates the log of co-occurrence probability:
- wᵢᵀw̃ⱼ + bᵢ + b̃ⱼ ≈ log(Xᵢⱼ)
- Minimize the following objective:
- J = Σᵢ,ⱼ f(Xᵢⱼ)(wᵢᵀw̃ⱼ + bᵢ + b̃ⱼ – log(Xᵢⱼ))²
Detailed Example
Imagine we’ve analyzed a large corpus and created a co-occurrence matrix:
| the | cat | sat | mat | |
|---|---|---|---|---|
| the | 0 | 45 | 12 | 32 |
| cat | 45 | 0 | 67 | 5 |
| sat | 12 | 67 | 0 | 56 |
| mat | 32 | 5 | 56 | 0 |
GloVe would find word vectors such that:
- vec(“cat”)·vec(“sat”) > vec(“cat”)·vec(“mat”) because cats sit more than they are on mats
- vec(“the”)·vec(“cat”) > vec(“the”)·vec(“sat”) because “the cat” is more common than “the sat”
After training, GloVe might produce 300-dimensional vectors that capture these statistical relationships. These vectors would support the same analogical reasoning as Word2Vec.
Mathematical Formulation
The GloVe objective function:
- J = Σᵢ,ⱼ f(Xᵢⱼ)(wᵢᵀw̃ⱼ + bᵢ + b̃ⱼ – log(Xᵢⱼ))²
Where:
- Xᵢⱼ is the co-occurrence count between words i and j
- wᵢ and w̃ⱼ are word and context vectors
- bᵢ and b̃ⱼ are bias terms
- f(Xᵢⱼ) is a weighting function:
- f(x) = (x/xₘₐₓ)^α if x < xₘₐₓ
- f(x) = 1 otherwise
Advantages
- Global Statistics: Captures both word-word relationships and corpus-level statistics
- Efficiency: More efficient use of statistics than Word2Vec
- Performance: Often outperforms Word2Vec on analogy tasks
- Explicit Modeling: Directly models co-occurrence probabilities
- Parallelizable: Training can be parallelized more effectively than neural methods
Disadvantages
- Static Embeddings: One representation per word, regardless of context
- Training Data: Requires substantial text data for good performance
- Memory Usage: Co-occurrence matrix can be massive for large vocabularies
- Out-of-Vocabulary: Cannot handle words not seen during training
- No Polysemy: Cannot represent multiple word senses
Practical Applications
- Document Classification: Improving classification accuracy
- Machine Translation: Enhancing translation quality
- Named Entity Recognition: Identifying entities in text
- Question Answering: Improving understanding of questions and contexts
- Transfer Learning: Providing pre-trained representations for other tasks
Code Implementation
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
# Simplified GloVe-style training (actual implementation would be more complex)
def train_simplified_glove(co_occurrence_matrix, vector_size=50, iterations=50, learning_rate=0.05):
vocab_size = co_occurrence_matrix.shape[0]
# Initialize random word and context vectors
W = np.random.randn(vocab_size, vector_size) * 0.01
W_context = np.random.randn(vocab_size, vector_size) * 0.01
b = np.zeros(vocab_size)
b_context = np.zeros(vocab_size)
# Training loop
for iteration in range(iterations):
cost = 0
for i in range(vocab_size):
for j in range(vocab_size):
if co_occurrence_matrix[i, j] > 0:
# Weight function - simplified
weight = min(1, (co_occurrence_matrix[i, j] / 100) ** 0.75)
# Compute prediction and error
prediction = np.dot(W[i], W_context[j]) + b[i] + b_context[j]
error = prediction - np.log(max(co_occurrence_matrix[i, j], 1))
# Update cost
cost += weight * error ** 2
# Compute gradients
grad = weight * error
# Update parameters
W[i] -= learning_rate * grad * W_context[j]
W_context[j] -= learning_rate * grad * W[i]
b[i] -= learning_rate * grad
b_context[j] -= learning_rate * grad
if iteration % 10 == 0:
print(f"Iteration {iteration}, Cost: {cost}")
# Final word vectors (sum of word and context vectors)
final_vectors = W + W_context
return final_vectors
# Example co-occurrence matrix
co_occurrence = np.array([
[0, 45, 12, 32],
[45, 0, 67, 5],
[12, 67, 0, 56],
[32, 5, 56, 0]
])
# Train simplified GloVe
word_vectors = train_simplified_glove(co_occurrence, vector_size=10, iterations=100)
# Calculate similarities
sim_matrix = cosine_similarity(word_vectors)
print("Word similarity matrix:")
print(sim_matrix)
# Example words
words = ["the", "cat", "sat", "mat"]
# Show most similar words for each word
for i, word in enumerate(words):
similarities = [(words[j], sim_matrix[i, j]) for j in range(len(words)) if j != i]
similarities.sort(key=lambda x: x[1], reverse=True)
print(f"Words most similar to '{word}': {similarities}")
6. Contextual Embeddings (BERT, ELMo, etc.)
Contextual embeddings revolutionized NLP by generating dynamic representations that capture the meaning of words in their specific context.
How It Works
Unlike static embeddings, contextual models:
- Process entire sentences/paragraphs together
- Use deep neural architectures (Transformers for BERT, bidirectional LSTMs for ELMo)
- Pre-train on massive corpora using tasks like masked language modeling
- Generate different vectors for the same word depending on its context
- Often use subword tokenization (WordPiece for BERT, Byte-Pair Encoding for others)
Detailed Example
Consider the word “bank” in different contexts:
- “I deposited money in the bank yesterday.”
- “We sat on the bank of the river and watched the sunset.”
With contextual embeddings:
- The model processes each full sentence
- “bank” in the first sentence gets a vector representing the financial institution meaning
- “bank” in the second sentence gets a different vector representing the river shore meaning
- These vectors capture the distinct meanings despite being the same word
For BERT specifically, before generating embeddings:
- The input is tokenized: “I deposited money in the bank yesterday.” → [“[CLS]”, “i”, “deposit”, “##ed”, “money”, “in”, “the”, “bank”, “yesterday”, “.”, “[SEP]”]
- Each token is assigned three embeddings (token, position, segment) which are summed
- This combined representation passes through multiple Transformer layers
- The final layer outputs contextualized embeddings for each token
Mathematical Formulation
For the BERT model, the attention mechanism is a key component:
- Attention(Q, K, V) = softmax(QK^T / √dₖ)V
Where Q, K, and V are query, key, and value matrices derived from the input embeddings.
The entire model consists of multiple layers of multi-headed attention and feed-forward networks:
- h₁ = LayerNorm(x + MultiHeadAttention(x))
- h₂ = LayerNorm(h₁ + FeedForward(h₁))
Advantages
- Context Awareness: Captures word meaning based on surrounding context
- Polysemy Handling: Different representations for different word senses
- Subword Tokenization: Handles out-of-vocabulary words effectively
- Deep Understanding: Captures complex language phenomena like negation
- State-of-the-Art Performance: Achieves best results on most NLP tasks
- Transfer Learning: Pre-trained models can be fine-tuned for specific tasks
Disadvantages
- Computational Requirements: Extremely resource-intensive
- Complexity: More difficult to implement and use
- Interpretability: Hard to understand what specific dimensions represent
- Size: Models are very large (hundreds of millions to billions of parameters)
- Training Data: Requires massive amounts of text for pre-training
Practical Applications
- Question Answering: Understanding questions and finding answers in text
- Text Classification: Superior document categorization
- Named Entity Recognition: Identifying and classifying entities
- Text Generation: Creating coherent and contextually appropriate text
- Sentiment Analysis: Understanding nuanced opinions and emotions
- Machine Translation: Producing high-quality translations
Code Implementation
import torch
from transformers import BertTokenizer, BertModel
# Load pre-trained model and tokenizer
tokenizer = BertTokenizer.from_pretrained('bert-base-uncased')
model = BertModel.from_pretrained('bert-base-uncased')
# Example sentences with the word "bank"
sentences = [
"I deposited money in the bank yesterday.",
"We sat on the bank of the river and watched the sunset."
]
# Get contextual embeddings for each sentence
for sentence in sentences:
# Tokenize and prepare for model
inputs = tokenizer(sentence, return_tensors="pt", padding=True, truncation=True)
# Get model outputs
with torch.no_grad():
outputs = model(**inputs)
# Get embeddings from last layer
embeddings = outputs.last_hidden_state
# Find the position of "bank" in tokenized input
tokens = tokenizer.convert_ids_to_tokens(inputs["input_ids"][0])
bank_position = tokens.index("bank")
# Extract the embedding for "bank"
bank_embedding = embeddings[0, bank_position].numpy()
print(f"\nContextual embedding for 'bank' in: \"{sentence}\"")
print(f"First 5 dimensions: {bank_embedding[:5]}...")
# Compare the two "bank" embeddings
bank1 = outputs.last_hidden_state[0, tokens.index("bank")].numpy()
tokens = tokenizer.convert_ids_to_tokens(tokenizer(sentences[1])["input_ids"])
inputs = tokenizer(sentences[1], return_tensors="pt")
with torch.no_grad():
outputs = model(**inputs)
bank2 = outputs.last_hidden_state[0, tokens.index("bank")].numpy()
# Calculate cosine similarity
cosine_sim = np.dot(bank1, bank2) / (np.linalg.norm(bank1) * np.linalg.norm(bank2))
print(f"\nCosine similarity between the two 'bank' embeddings: {cosine_sim}")
print(f"Note that this value would be 1.0 with static embeddings like Word2Vec")
7. FastText
FastText extends Word2Vec by incorporating subword information, making it better at handling rare and unseen words.
How It Works
- Represents each word as a bag of character n-grams (plus the word itself)
- Each n-gram has its own vector representation
- A word’s embedding is the sum of its n-gram vectors
- Uses similar training approaches as Word2Vec (Skip-gram or CBOW)
Detailed Example
For the word “apple” with n-grams of length 3-6:
- Character n-grams: “<ap”, “app”, “ppl”, “ple”, “le>”, “<app”, “appl”, “pple”, “ple>”, “<appl”, “apple”, “pple>”, “<apple”, “apple>”
- (where < and > represent word boundaries)
The final vector for “apple” would be the sum of these n-gram vectors plus the vector for the whole word.
When encountering an unseen word like “applet”:
- Many n-grams overlap with “apple” (e.g., “app”, “ppl”)
- FastText can build a reasonable embedding from these shared n-grams
- This gives better coverage for rare, technical, or misspelled words
Advantages
- Morphological Awareness: Captures word structure and morphology
- Out-of-Vocabulary Handling: Can generate embeddings for unseen words
- Robustness to Misspellings: Similar embeddings for misspelled variants
- Better for Morphologically Rich Languages: Works well for languages with many word forms
- Compact Models: Can be compressed efficiently
Disadvantages
- Larger Models: More parameters than Word2Vec
- Computational Cost: More expensive to train
- Still Static: No context sensitivity despite subword awareness
- Less Semantic Precision: May blur distinctions between some similar words
Code Implementation
from gensim.models import FastText
# Sample corpus
sentences = [
["the", "quick", "brown", "fox", "jumps", "over", "the", "lazy", "dog"],
["the", "brown", "fox", "is", "quick", "and", "the", "dog", "is", "lazy"],
["quick", "brown", "foxes", "jump", "over", "lazy", "dogs"]
]
# Train model
model = FastText(sentences, vector_size=100, window=5, min_count=1, workers=4, min_n=3, max_n=6)
# Explore word vectors
print(f"Vector for 'fox': {model.wv['fox'][:5]}...") # Show first 5 dimensions
# Find similar words
similar_words = model.wv.most_similar("fox", topn=3)
print(f"Words similar to 'fox': {similar_words}")
# Out-of-vocabulary word handling
print(f"Vector for unseen word 'foxiest': {model.wv['foxiest'][:5]}...")
8. Doc2Vec (Paragraph Vector)
Doc2Vec extends Word2Vec to learn fixed-length representations for variable-length texts such as sentences, paragraphs, or documents.
How It Works
Doc2Vec has two main variants:
- Distributed Memory (DM):
- Similar to CBOW in Word2Vec
- Predicts a target word given context words AND a document vector
- The document vector serves as a memory that captures the topic of the document
- Distributed Bag of Words (DBOW):
- Similar to Skip-gram in Word2Vec
- Predicts context words given only the document vector
- Simpler but often works as well as DM
Detailed Example
Consider training Doc2Vec on a corpus of movie reviews:
- Assign a unique ID to each review
- Train the model to predict words in the review given the review ID
- The resulting vectors for each review ID capture the semantic content
For example, reviews about action movies will have similar vectors, distinct from those about romantic comedies.
After training, we can:
- Compare documents directly (e.g., find similar movie reviews)
- Infer vectors for new, unseen documents
- Use document vectors for classification or clustering
Advantages
- Document-Level Semantics: Captures meaning at document scale
- Fixed-Length Representation: Consistent size regardless of document length
- Compositionality: Combines word and document meaning
- End-to-End Learning: Learns document representations directly
- Unsupervised: Doesn’t require labeled data
8. Doc2Vec (Paragraph Vector) (continued)
Disadvantages
- Training Complexity: More complex to train than word embeddings
- Data Requirements: Needs substantial corpus for good representations
- Hyperparameter Sensitivity: Performance varies with parameter settings
- Black Box: Difficult to interpret what dimensions represent
- No Context Within Documents: Treats all words in document equally
Practical Applications
- Document Classification: Categorizing texts by topic or sentiment
- Information Retrieval: Finding similar documents
- Document Clustering: Grouping similar texts
- Recommendation Systems: Suggesting similar content
- Plagiarism Detection: Identifying semantically similar documents
Code Implementation
from gensim.models.doc2vec import Doc2Vec, TaggedDocument
from nltk.tokenize import word_tokenize
# Sample corpus
documents = [
"The quick brown fox jumps over the lazy dog",
"The fox is quick and the dog is lazy",
"Quick brown foxes jump over lazy dogs",
"I love machine learning and natural language processing",
"Vector representations are useful in NLP tasks",
"Natural language processing involves machine learning"
]
# Preprocess and tag documents
tagged_docs = [TaggedDocument(words=word_tokenize(doc.lower()), tags=[i])
for i, doc in enumerate(documents)]
# Train model
model = Doc2Vec(vector_size=50, min_count=1, epochs=40)
model.build_vocab(tagged_docs)
model.train(tagged_docs, total_examples=model.corpus_count, epochs=model.epochs)
# Explore document vectors
print(f"Vector for document 0: {model.dv[0][:5]}...") # Show first 5 dimensions
# Find similar documents
similar_docs = model.dv.most_similar(0, topn=2)
print(f"Documents similar to document 0: {similar_docs}")
# Infer vector for a new document
new_doc = "Foxes and dogs are quick animals"
inferred_vector = model.infer_vector(word_tokenize(new_doc.lower()))
print(f"Inferred vector for new document: {inferred_vector[:5]}...")
# Find similar documents to the new document
similar_to_new = model.dv.most_similar([inferred_vector], topn=2)
print(f"Documents similar to new document: {similar_to_new}")
9. Universal Sentence Encoder (USE)
The Universal Sentence Encoder provides sentence-level embeddings that scale to various NLP tasks with minimal task-specific training data.
How It Works
USE has two major variants:
- Transformer-based:
- Uses a Transformer architecture similar to BERT
- Optimizes for accuracy at the cost of computational complexity
- Processes full sentences with attention mechanisms
- DAN-based (Deep Averaging Network):
- Averages embeddings for input words/n-grams and passes through a deep neural network
- More efficient but slightly less accurate
- Better suited for mobile and low-resource environments
Both are trained on a variety of tasks, including:
- Skip-thought prediction
- Translation ranking
- Natural language inference
- Conversational response prediction
Detailed Example
Consider two sentences:
- “The cat sat on the mat.”
- “A feline rested on the floor covering.”
Despite different vocabulary, USE would produce similar embeddings for these semantically similar sentences.
When applied to question answering:
- Question: “What is the capital of France?”
- Candidate answers from a knowledge base are encoded
- The answer with the highest cosine similarity to the question is selected
- “Paris is the capital of France” would have high similarity
Advantages
- Sentence-Level Semantics: Captures meaning at sentence scale
- Transfer Learning Ready: Pre-trained for use across multiple tasks
- Minimal Fine-tuning: Works well with limited task-specific data
- Language Understanding: Captures semantic similarities regardless of phrasing
- Multilingual Versions: Available for multiple languages
Disadvantages
- Fixed Representation: One vector per sentence regardless of length
- Computational Requirements: Transformer variant is resource-intensive
- Limited Context Length: Performance degrades with very long texts
- Black Box: Difficult to interpret dimensions
- Less Precise Than Task-Specific Models: Jack-of-all-trades approach
Practical Applications
- Semantic Textual Similarity: Measuring how similar two texts are
- Clustering: Grouping similar sentences or paragraphs
- Classification: Categorizing short texts
- Information Retrieval: Finding relevant information from a corpus
- Semantic Search: Searching by meaning rather than keywords
Code Implementation
import tensorflow as tf
import tensorflow_hub as hub
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
# Load pre-trained USE model
embed = hub.load("https://tfhub.dev/google/universal-sentence-encoder/4")
# Example sentences
sentences = [
"The cat sat on the mat.",
"A feline rested on the floor covering.",
"Dogs chase cats.",
"What is the capital of France?",
"Paris is the capital of France."
]
# Generate embeddings
embeddings = embed(sentences)
print(f"Embedding shape: {embeddings.shape}") # Should be (5, 512)
# Compute similarity matrix
similarity_matrix = cosine_similarity(embeddings)
print("Similarity matrix:")
for i in range(len(sentences)):
for j in range(i+1, len(sentences)):
print(f"Similarity between \"{sentences[i]}\" and \"{sentences[j]}\": {similarity_matrix[i, j]:.4f}")
# Question answering example
question = "What is the capital of France?"
question_embedding = embed([question])
candidate_answers = [
"Paris is the capital of France.",
"Berlin is the capital of Germany.",
"London is the capital of England."
]
answer_embeddings = embed(candidate_answers)
# Calculate similarities between question and answers
similarities = cosine_similarity(question_embedding, answer_embeddings)[0]
for i, (answer, similarity) in enumerate(zip(candidate_answers, similarities)):
print(f"Answer {i+1}: \"{answer}\" - Similarity: {similarity:.4f}")
# Get best answer
best_answer_index = np.argmax(similarities)
print(f"Best answer: \"{candidate_answers[best_answer_index]}\"")
10. Sentence-BERT (SBERT)
Sentence-BERT modifies the BERT architecture to derive semantically meaningful sentence embeddings efficiently.
How It Works
- Uses siamese and triplet network structures with BERT/RoBERTa/etc. as base models
- Applies pooling to the output of BERT (mean, max, or CLS token pooling)
- Trained on sentence pairs with objectives like:
- Natural Language Inference (entailment, contradiction, neutral)
- Semantic Textual Similarity (scoring sentence similarity)
- Produces fixed-size sentence embeddings optimized for semantic comparison
Detailed Example
Training process example:
- Take sentence pairs labeled for similarity
- “I love pizza” and “Pizza is my favorite food” (similar)
- “I love pizza” and “I hate vegetables” (dissimilar)
- Pass both sentences through the same BERT model with shared weights
- Apply pooling to get a fixed vector for each sentence
- Train the network to minimize distance between similar sentences and maximize distance between dissimilar ones
In practice:
- Computing similarity between 10,000 sentences using BERT would require 50 million sentence pair computations
- With SBERT, each sentence is encoded once and similarities are computed via vector operations, reducing computation by 99.8%
Mathematical Formulation
For the triplet objective function:
- L = max(0, ||a-p||² – ||a-n||² + margin)
Where:
- a is the anchor sentence embedding
- p is a positive example (similar sentence)
- n is a negative example (dissimilar sentence)
- margin is a hyperparameter that enforces a minimum distance
Advantages
- Efficiency: Much faster than comparing all sentence pairs with BERT
- Semantic Understanding: Captures sentence meaning well
- Strong Transfer Learning: Pre-trained models work well across domains
- State-of-the-art Performance: Achieves excellent results on sentence similarity tasks
- Handles Longer Text: Better than word embeddings for sentences
- Task Adaptability: Can be fine-tuned for specific tasks
Disadvantages
- Resource Requirements: Still needs significant computational resources
- Limited Context Length: Performance decreases with very long texts
- Black Box Nature: Difficult to interpret what dimensions represent
- Fixed Embedding Size: Same dimensionality regardless of sentence complexity
- Domain Adaptation Challenges: May require fine-tuning for specialized domains
Practical Applications
- Semantic Search: Finding relevant documents quickly
- Clustering: Grouping similar texts efficiently
- Information Retrieval: Retrieving relevant information
- Paraphrase Mining: Finding alternative expressions of the same idea
- Automatic Essay Grading: Comparing student answers to reference answers
- Duplicate Question Detection: Finding similar questions on Q&A platforms
Code Implementation
from sentence_transformers import SentenceTransformer, util
# Load pre-trained SBERT model
model = SentenceTransformer('all-MiniLM-L6-v2')
# Example sentences
sentences = [
"The cat sat on the mat.",
"A feline rested on the floor covering.",
"Dogs chase cats.",
"What is the capital of France?",
"Paris is the capital of France."
]
# Generate embeddings
embeddings = model.encode(sentences)
print(f"Embedding shape: {embeddings.shape}") # Should be (5, 384)
# Compute similarity matrix
similarity_matrix = util.cos_sim(embeddings, embeddings)
print("Similarity matrix:")
for i in range(len(sentences)):
for j in range(i+1, len(sentences)):
print(f"Similarity between \"{sentences[i]}\" and \"{sentences[j]}\": {similarity_matrix[i, j].item():.4f}")
# Semantic search example
query = "What is the capital of France?"
query_embedding = model.encode([query])
corpus = [
"Paris is the capital of France.",
"Berlin is the capital of Germany.",
"London is the capital of England."
]
corpus_embeddings = model.encode(corpus)
# Calculate similarities between query and corpus
hits = util.semantic_search(query_embedding, corpus_embeddings, top_k=3)
for hit in hits[0]:
print(f"Score: {hit['score']:.4f} - \"{corpus[hit['corpus_id']]}\"")
Comparison of Text Representation Techniques
| Technique | Dimensionality | Context Awareness | OOV Handling | Semantic Capture | Computational Cost | Best For |
|---|---|---|---|---|---|---|
| One-Hot Encoding | Very High (vocab size) | None | Poor | None | Low | Basic preprocessing |
| Bag of Words | High (vocab size) | None | Poor | None | Low | Simple classification |
| TF-IDF | High (vocab size) | None | Poor | Limited | Low | Information retrieval |
| Word2Vec | Medium (100-300) | None | Poor | Good | Medium | Word similarity, analogies |
| GloVe | Medium (100-300) | None | Poor | Good | Medium | Word semantics, analogies |
| FastText | Medium (100-300) | None | Good | Good | Medium-High | Morphologically rich languages |
| Doc2Vec | Medium (100-300) | Document-level | Poor | Good | Medium | Document classification |
| BERT/Contextual | High (768+) | Excellent | Good | Excellent | Very High | Complex NLP tasks |
| Universal Sentence Encoder | Medium (512) | Sentence-level | Medium | Very Good | Medium-High | Sentence comparison |
| Sentence-BERT | Medium (384-768) | Sentence-level | Good | Excellent | High | Efficient semantic search |
Practical Selection Guide
When to Use Each Technique
- One-Hot Encoding:
- Teaching concepts
- Very small vocabularies
- When explicit word identity is critical
- Bag of Words:
- Simple text classification tasks
- When word order doesn’t matter
- Limited computational resources
- Easily interpretable models
- TF-IDF:
- Search engine relevance ranking
- When distinctive words matter more than common ones
- Document similarity measures
- Topic extraction
- Word2Vec/GloVe:
- When word relationships matter
- Transfer learning for limited datasets
- Exploration of semantic relationships
- Moderate computational resources
- FastText:
- Languages with rich morphology
- When handling rare words is important
- When misspellings are common
- Social media text with neologisms
- Doc2Vec:
- Document-level tasks
- When document identity matters more than individual words
- Recommendation systems
- Plagiarism detection
- BERT/Contextual Embeddings:
- Complex language understanding tasks
- When word sense disambiguation is critical
- When context significantly changes meaning
- When state-of-the-art performance is required
- Universal Sentence Encoder:
- Cross-domain sentence comparison
- Limited fine-tuning data available
- Mobile or resource-constrained environments (DAN version)
- Quick prototyping of sentence-level applications
- Sentence-BERT:
- Large-scale semantic search
- Efficient clustering of many sentences
- Real-time similarity computation
- Production systems requiring sentence embeddings
Implementation Considerations
Data Preprocessing
Regardless of the technique chosen, proper text preprocessing is crucial:
- Tokenization: Breaking text into words, subwords, or characters
- Lowercasing: Converting all text to lowercase (usually)
- Stopword Removal: Removing common words with little semantic value (for non-neural methods)
- Stemming/Lemmatization: Reducing words to base forms (for non-neural methods)
- Special Character Handling: Deciding how to treat punctuation, numbers, etc.
- Handling Out-of-Vocabulary Words: Creating strategies for unseen words
Evaluation Metrics
When comparing text representation techniques, consider these metrics:
- Intrinsic Evaluation:
- Word/Sentence Similarity Correlation
- Analogy Task Accuracy
- Word/Document Clustering Quality
- Extrinsic Evaluation:
- Downstream Task Performance
- Classification Accuracy
- Retrieval Precision/Recall
- Machine Translation BLEU Scores
Hybrid Approaches
Often, the best solution combines multiple techniques:
- Ensemble Methods: Using multiple representation types and combining predictions
- Feature Stacking: Concatenating different embeddings
- Task-Specific Fine-Tuning: Starting with pre-trained embeddings and adapting to domain
- Multi-level Representations: Using word, sentence, and document embeddings together
Conclusion
Text representation has evolved dramatically from simple one-hot encoding to sophisticated contextual embedding models. Each technique offers unique trade-offs between simplicity, computational efficiency, and semantic understanding.
For practical applications:
- Consider your computational constraints
- Evaluate the importance of contextual understanding
- Assess the availability of training data
- Balance accuracy requirements against implementation complexity
The field continues to advance rapidly, with contextual embeddings and their efficient derivatives currently representing the state-of-the-art for most applications. However, simpler techniques like TF-IDF and non-contextual word embeddings remain valuable for specific use cases, especially when computational resources are limited or when interpretability is important.
By understanding the full spectrum of text representation techniques, NLP practitioners can make informed choices for their specific applications, leading to more effective and efficient text processing systems.

Containerizing a Flask Project with Docker: A Comprehensive Guide
Containerization has revolutionized how we deploy and scale applications. In this blog post, I’ll walk you through the complete process of containerizing a Flask application using Docker, focusing on the AQI (Air Quality Index) app as a practical example. We’ll cover everything from basic Docker concepts to advanced multi-container deployments with various services.
Understanding Docker Fundamentals
Before diving into the practical steps, let’s clarify some key Docker concepts:
What is a Container?
A container is a lightweight, standalone, executable software package that includes everything needed to run an application: code, runtime, system tools, libraries, and settings. Containers isolate software from its environment, ensuring it works uniformly across different computing environments.
What is a Docker Image?
A Docker image is a read-only template that contains a set of instructions for creating a container. It’s essentially a snapshot of a container that includes the application code, libraries, dependencies, tools, and other files needed for the application to run.
The Relationship Between Images and Containers
Think of a Docker image as a class in object-oriented programming, and a container as an instance of that class. From a single image, you can create multiple running containers, each isolated from the others.
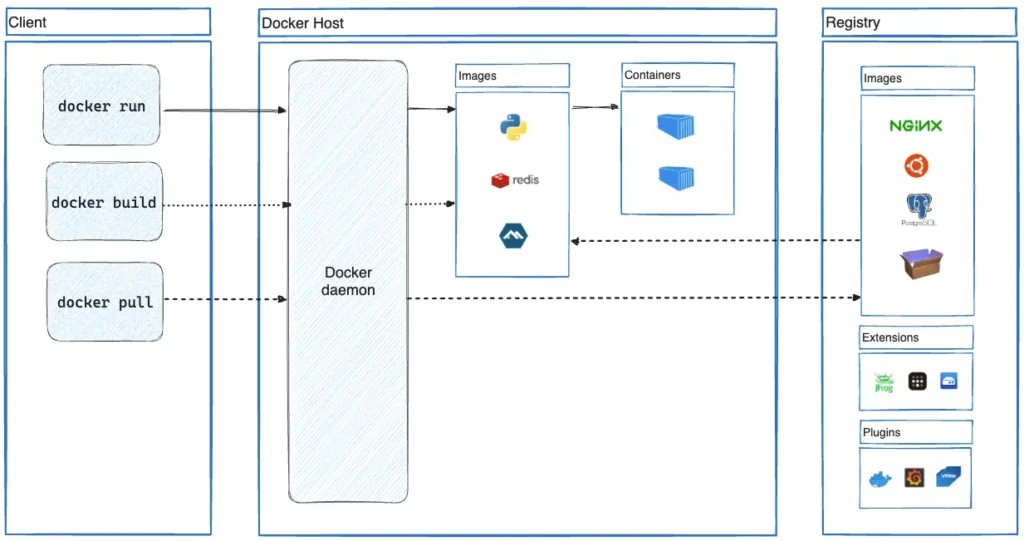
Setting Up Docker
Let’s start by getting Docker installed and ready on your system.
Installing Docker
For Ubuntu/Debian-based systems:
sudo apt update
sudo apt install docker.io docker-compose
sudo systemctl enable --now docker
sudo usermod -aG docker $USERFor macOS and Windows, download and install Docker Desktop from the official Docker website.
Verifying Installation
After installation, verify Docker is working correctly:
docker --version
docker-compose --version
docker run hello-worldContainerizing the Flask AQI Application
Now, let’s explore how to containerize our Flask AQI application step by step.
Creating a Dockerfile
The Dockerfile is a script containing instructions to build a Docker image. Create a file named Dockerfile in your project’s root directory:
dockerfileCopy# Use an official Python runtime as a parent image
FROM python:3.9-slim
# Set the working directory in the container
WORKDIR /app
# Copy the current directory contents into the container at /app
COPY . /app/
# Install any needed packages specified in requirements.txt
RUN pip install --no-cache-dir -r requirements.txt
# Make port 5000 available to the world outside this container
EXPOSE 5000
# Define environment variable
ENV FLASK_APP=app.py
ENV FLASK_RUN_HOST=0.0.0.0
# Run app.py when the container launches
CMD ["flask", "run"]Creating a .dockerignore File
To prevent unnecessary files from being included in your Docker image, create a .dockerignore file:
__pycache__/
*.pyc
*.pyo
*.pyd
.Python
env/
venv/
.venv/
ENV/
env.bak/
venv.bak/
.git
.gitignore
.env
.dockerignore
Dockerfile
*.mdBuilding the Docker Image
Build the Docker image with the following command:
docker build -t aqi-flask-app .This command creates an image named “aqi-flask-app” from the current directory (.).
Running the Container
Start a container from the image with:
docker run -d -p 5000:5000 --name aqi-container aqi-flask-appThis command:
-d: Runs the container in detached mode (in the background)-p 5000:5000: Maps port 5000 of the container to port 5000 on the host--name aqi-container: Names the container “aqi-container”aqi-flask-app: Specifies the image to use
Basic Docker Management Commands
Here are some useful commands to manage your Docker containers and images:
# List running containers
docker ps
# List all containers (including stopped ones)
docker ps -a
# Stop a container
docker stop aqi-container
# Start a stopped container
docker start aqi-container
# Remove a container
docker rm aqi-container
# List all images
docker images
# Remove an image
docker rmi aqi-flask-app
# View container logs
docker logs aqi-container
# Execute a command in a running container
docker exec -it aqi-container bashUsing Docker Compose for Multi-Container Applications
For applications requiring multiple services (like a web server, database, cache, etc.), Docker Compose simplifies management.
Creating a docker-compose.yml File
Create a docker-compose.yml file in your project root:
docker-compose.ymlCode
Launching the Application with Docker Compose
Start all services with a single command:
docker-compose up -dTo stop and remove all containers:
docker-compose downUnderstanding the Services
Let’s explore each service used in our Docker Compose setup:
Web Service
This is our Flask application container. It builds from the Dockerfile in the current directory and exposes port 5000. Environment variables configure the Flask app and connection strings for the other services. The volume mapping allows for code changes without rebuilding the image during development.
Redis Service
Redis is an in-memory data structure store, often used as a database, cache, or message broker. In our AQI application, Redis could be used for:
- Caching API responses to reduce external API calls
- Storing session data
- Rate limiting API requests
- Implementing a publish-subscribe pattern for real-time updates
The Redis service uses the official Redis Alpine image, which is lightweight and secure. Data persistence is configured through a volume.
MongoDB Service
MongoDB is a NoSQL document database that stores data in flexible, JSON-like documents. It’s ideal for applications with evolving data requirements. In our AQI app, MongoDB might store:
- Historical AQI readings
- User preferences and settings
- Location data
The volume ensures data persists beyond container lifecycles.
MySQL Service
MySQL is a traditional relational database management system. In our application, MySQL could handle:
- User authentication and authorization
- Structured data with relationships
- Transactional data that requires ACID compliance
Environment variables configure the database, user, and password.
Advanced Docker Techniques
Let’s explore some advanced Docker techniques for optimizing our containerized application.
Multi-Stage Builds
Multi-stage builds can significantly reduce image size by separating build-time dependencies from runtime dependencies:
# Build stage
FROM python:3.9 AS builder
WORKDIR /build
COPY requirements.txt .
RUN pip wheel --no-cache-dir --no-deps --wheel-dir /build/wheels -r requirements.txt
# Runtime stage
FROM python:3.9-slim
WORKDIR /app
COPY --from=builder /build/wheels /wheels
COPY --from=builder /build/requirements.txt .
RUN pip install --no-cache /wheels/*
COPY . .
EXPOSE 5000
ENV FLASK_APP=app.py
ENV FLASK_RUN_HOST=0.0.0.0
CMD ["flask", "run"]Health Checks
Adding health checks ensures Docker only sends traffic to healthy containers:
HEALTHCHECK --interval=30s --timeout=3s \
CMD curl -f http://localhost:5000/health || exit 1Add this to your Dockerfile or in docker-compose.yml:
services:
web:
# ... other configuration
healthcheck:
test: ["CMD", "curl", "-f", "http://localhost:5000/health"]
interval: 30s
timeout: 3s
retries: 3
start_period: 40sContainer Networking
Docker Compose automatically creates a network for your application. Services can communicate using their service names as hostnames. For example, in your Flask app, you can connect to Redis using:
import redis
r = redis.Redis(host='redis', port=6379)Deploying the Containerized Application
Let’s look at different deployment options for our containerized application.
Deploying to Docker Hub
First, tag your image with your Docker Hub username:
docker tag aqi-flask-app tejask0512/aqi-app:latestLogin to Docker Hub and push your image:
docker login
docker push tejask0512/aqi-app:latestUsing the Shared Docker Image
You can directly use the pre-built image mentioned in your question:
docker pull tejask0512/aqi-app
docker run -d -p 5000:5000 tejask0512/aqi-appOr in docker-compose.yml, replace the build directive with:
web:
image: tejask0512/aqi-app:latest
# rest of configurationDeploying to Production Environments
For production, consider the following modifications:
- Set environment variables appropriately:
environment:
- FLASK_ENV=production
- FLASK_DEBUG=0- Use Docker secrets or environment files for sensitive data:
docker-compose --env-file production.env up -d- Set resource limits:
services:
web:
# ... other configuration
deploy:
resources:
limits:
cpus: '0.50'
memory: 512MDocker Volumes for Data Persistence
Our docker-compose.yml already includes volumes, but let’s explain them in more detail:
Types of Docker Volumes
- Named Volumes: What we’re using in our compose file. Docker manages these volumes automatically.
- Bind Mounts: Map a host directory to a container directory:
volumes:
- ./host/path:/container/path- tmpfs Mounts: Store data in the host’s memory:
volumes:
- type: tmpfs
target: /app/cacheManaging Volumes
View all volumes:
docker volume lsCreate a volume:
docker volume create aqi_dataInspect a volume:
docker volume inspect redis_dataRemove unused volumes:
docker volume pruneMonitoring and Logging
For production applications, proper monitoring and logging are essential.
Viewing Container Logs
# View logs for a specific container
docker logs aqi-container
# Follow logs (stream in real-time)
docker logs -f aqi-container
# Show logs generated in the last hour
docker logs --since=1h aqi-containerUsing Docker Stats
Monitor container resource usage:
docker statsIntegrating with External Monitoring Tools
For more comprehensive monitoring, you might integrate with:
- Prometheus and Grafana:
services:
prometheus:
image: prom/prometheus
volumes:
- ./prometheus.yml:/etc/prometheus/prometheus.yml
ports:
- "9090:9090"
grafana:
image: grafana/grafana
ports:
- "3000:3000"
depends_on:
- prometheus- ELK Stack (Elasticsearch, Logstash, Kibana) for log aggregation and analysis.
Security Best Practices
Here are some security practices to follow when working with Docker:
- Run containers as non-root users:
# Create non-root user
RUN addgroup --system app && adduser --system --group app
USER app- Scan images for vulnerabilities:
docker scan aqi-flask-app- Use specific image tags instead of “latest” to ensure reproducibility.
- Limit container capabilities: .yaml
services:
web:
cap_drop:
- ALL
cap_add:
- NET_BIND_SERVICE- Use secrets management for sensitive information like API keys and passwords.
Optimizing Docker Images
To reduce image size and improve security:
- Use minimal base images like alpine or slim variants.
- Clean up in the same layer where you install: dockerfile
RUN apt-get update && \
apt-get install -y some-package && \
apt-get clean && \
rm -rf /var/lib/apt/lists/*- Minimize the number of layers by combining commands.
- Remove development dependencies in production builds.
Continuous Integration/Continuous Deployment (CI/CD)
Integrate Docker with CI/CD pipelines for automated testing and deployment:
Sample GitHub Actions Workflow: .yaml
name: Docker CI/CD
on:
push:
branches: [ main ]
jobs:
build-and-deploy:
runs-on: ubuntu-latest
steps:
- uses: actions/checkout@v2
- name: Set up Docker Buildx
uses: docker/setup-buildx-action@v1
- name: Login to DockerHub
uses: docker/login-action@v1
with:
username: ${{ secrets.DOCKER_HUB_USERNAME }}
password: ${{ secrets.DOCKER_HUB_TOKEN }}
- name: Build and push
uses: docker/build-push-action@v2
with:
push: true
tags: tejask0512/aqi-app:latestTroubleshooting Common Docker Issues
Container Won’t Start
Check the logs:
docker logs aqi-containerCheck if ports are already in use:
sudo lsof -i :5000Container Starts but Application Isn’t Accessible
Verify network settings:
docker network inspect bridgeMake sure the application is binding to 0.0.0.0, not localhost or 127.0.0.1.
Out of Disk Space
Clean up unused Docker resources:
docker system prune -aPerformance Issues
Monitor resource usage:
docker statsConsider setting appropriate resource limits in docker-compose.yml.
Conclusion
Containerizing applications with Docker transforms the way we develop, deploy, and scale software. Whether you’re working with a simple Flask application or a complex microservices architecture, Docker provides the tools to manage your infrastructure effectively.
By following the practices outlined in this guide, you can build, deploy, and manage containerized applications with confidence. The AQI app example demonstrates how different services can work together seamlessly in a Docker environment, providing a foundation you can build upon for your own projects.
Remember, containerization is not just about wrapping your application in Docker – it’s about embracing an entire ecosystem of tools and practices that make your applications more reliable, scalable, and easier to manage.
Would you like me to explain any particular section of this guide in more detail?

Statistics for Machine Learning (Required statistics for Machine learning)
The basic and most important part of the Machine learning and Data analysis is to understand the Data, Analyze the pattern in technical way we will say distribution of the data, we will discuss as follow:
To understand the machine learning and data science perfectly you must know the statistics. we are going to discuss most important techniques in the Statistics.
Types of Statistics:
- Descriptive
- Inferential
Descriptive Statistics:
1) Measure of Central Tendencies (Mean, Median, Mode)
Measures of central tendency are statistical metrics that summarize a dataset by identifying its central point. They provide insights into the “typical” or “average” value in a dataset, making them essential for analyzing and comparing data distributions.
There are three main measures of central tendency: Mean, Median, and Mode.
1. Mean (Arithmetic Average)
The mean is the sum of all values in a dataset divided by the number of values. It is the most commonly used measure of central tendency.
Formula
For a dataset with nnn values: Mean(xˉ)=∑xin\text{Mean} (\bar{x}) = \frac{\sum x_i}{n}Mean(xˉ)=n∑xi
where:
- xix_ixi represents individual values,
- nnn is the total number of values.
Example
Consider the dataset: {4, 8, 10, 12, 14} xˉ=4+8+10+12+145=485=9.6\bar{x} = \frac{4 + 8 + 10 + 12 + 14}{5} = \frac{48}{5} = 9.6xˉ=54+8+10+12+14=548=9.6
Thus, the mean is 9.6.
Pros and Cons
✅ Easy to calculate and widely used.
✅ Considers all values in the dataset.
❌ Sensitive to outliers (e.g., extreme values can skew the mean).
2. Median (Middle Value of a Sorted Dataset)
The median is the middle value when the dataset is arranged in ascending or descending order. If there are an odd number of values, the median is the middle one. If there are an even number of values, the median is the average of the two middle values.
Steps to Find the Median
- Sort the dataset in ascending order.
- If nnn is odd, the median is the middle value: Median=x(n+12)\text{Median} = x_{\left(\frac{n+1}{2}\right)}Median=x(2n+1)
- If nnn is even, the median is the average of the two middle values: Median=x(n2)+x(n2+1)2\text{Median} = \frac{x_{\left(\frac{n}{2}\right)} + x_{\left(\frac{n}{2} + 1\right)}}{2}Median=2x(2n)+x(2n+1)
Example 1 (Odd Number of Values)
Dataset: {3, 7, 9, 11, 15}
- Middle value: 9 (third value in sorted order).
- Median = 9
Example 2 (Even Number of Values)
Dataset: {2, 5, 8, 12, 14, 18}
- Middle two values: 8 and 12
- Median: 8+122=10\frac{8 + 12}{2} = 1028+12=10
- Median = 10
Pros and Cons
✅ Not affected by outliers, making it a good measure for skewed distributions.
✅ Works well for ordinal data.
❌ Ignores extreme values in the dataset.
3. Mode (Most Frequent Value)
The mode is the value that appears most frequently in a dataset. A dataset can have:
- No mode (if all values appear once).
- One mode (Unimodal dataset).
- Two modes (Bimodal dataset).
- More than two modes (Multimodal dataset).
Example 1 (Unimodal Dataset)
Dataset: {2, 4, 4, 6, 8, 10}
- The number 4 appears twice, making it the mode.
- Mode = 4
Example 2 (Bimodal Dataset)
Dataset: {1, 3, 3, 5, 7, 7, 9}
- Two numbers appear most frequently: 3 and 7.
- Modes = 3 and 7 (Bimodal)
Example 3 (No Mode)
Dataset: {2, 5, 8, 11, 14}
- No repeated values, so no mode exists.
Pros and Cons
✅ Useful for categorical data (e.g., finding the most common brand, product, or category).
✅ Works well for non-numeric data.
❌ May not exist or may be multiple, making interpretation difficult.
Choosing the Best Measure of Central Tendency
| Scenario | Best Measure |
|---|---|
| Symmetric data with no outliers | Mean |
| Skewed data with outliers | Median |
| Categorical or qualitative data | Mode |
| Bimodal/multimodal distribution | Mode |
Example: House Prices
Consider the house prices (in $1000s):
{120, 130, 135, 140, 500}
- Mean = 120+130+135+140+5005=205\frac{120+130+135+140+500}{5} = 2055120+130+135+140+500=205 (highly affected by outlier).
- Median = 135 (middle value, better representation).
- Mode = No mode (no repetition).
In this case, the median is the best measure because it is unaffected by the extreme value (500).
2) Measure of Dispersion (Standard Deviation, Variance)
1. Measures of Dispersion
While measures of central tendency (mean, median, mode) tell us about the center of the data, measures of dispersion describe how spread out the data points are. The most common measures of dispersion include Variance and Standard Deviation.
1.1 Variance (𝜎² or s²)
Variance measures how much each data point deviates from the mean, squared.
Formulas for Variance
- Population Variance (𝜎²) σ2=∑(xi−μ)2N\sigma^2 = \frac{\sum (x_i – \mu)^2}{N}σ2=N∑(xi−μ)2 where:
- σ2\sigma^2σ2 = population variance
- xix_ixi = individual data points
- μ\muμ = population mean
- NNN = total number of data points in the population
- Sample Variance (s²) s2=∑(xi−xˉ)2n−1s^2 = \frac{\sum (x_i – \bar{x})^2}{n – 1}s2=n−1∑(xi−xˉ)2 where:
- s2s^2s2 = sample variance
- xˉ\bar{x}xˉ = sample mean
- nnn = sample size
🔹 Why use (n-1) in the sample variance formula?
The denominator (n−1)(n-1)(n−1) is known as Bessel’s correction, which corrects for bias in estimating the population variance from a sample.
1.2 Standard Deviation (𝜎 or s)
Standard deviation is simply the square root of variance. It provides a measure of spread in the same units as the data.
Formulas for Standard Deviation
- Population Standard Deviation σ=∑(xi−μ)2N\sigma = \sqrt{\frac{\sum (x_i – \mu)^2}{N}}σ=N∑(xi−μ)2
- Sample Standard Deviation s=∑(xi−xˉ)2n−1s = \sqrt{\frac{\sum (x_i – \bar{x})^2}{n – 1}}s=n−1∑(xi−xˉ)2
Example Calculation: Consider the dataset {10, 12, 14, 18, 20}
- Find the mean: xˉ=10+12+14+18+205=14.8\bar{x} = \frac{10+12+14+18+20}{5} = 14.8xˉ=510+12+14+18+20=14.8
- Calculate squared deviations from the mean: (10−14.8)2=23.04,(12−14.8)2=7.84,(14−14.8)2=0.64(10 – 14.8)^2 = 23.04, \quad (12 – 14.8)^2 = 7.84, \quad (14 – 14.8)^2 = 0.64(10−14.8)2=23.04,(12−14.8)2=7.84,(14−14.8)2=0.64 (18−14.8)2=10.24,(20−14.8)2=27.04(18 – 14.8)^2 = 10.24, \quad (20 – 14.8)^2 = 27.04(18−14.8)2=10.24,(20−14.8)2=27.04
- Find Variance: s2=23.04+7.84+0.64+10.24+27.045−1=68.84=17.2s^2 = \frac{23.04 + 7.84 + 0.64 + 10.24 + 27.04}{5 – 1} = \frac{68.8}{4} = 17.2s2=5−123.04+7.84+0.64+10.24+27.04=468.8=17.2
- Find Standard Deviation: s=17.2≈4.15s = \sqrt{17.2} \approx 4.15s=17.2≈4.15
Thus, the sample standard deviation is 4.15.
2. Population vs. Sample
2.1 Population
A population includes all members of a defined group. When we calculate statistics for an entire population, we use N in the denominator.
Example: The average height of all people in a country.
2.2 Sample
A sample is a subset of a population. Since we usually cannot collect data from the entire population, we estimate statistics using a sample and use n-1 in the denominator.
Example: Measuring the height of 1,000 randomly selected people to estimate the national average.
3. Types of Variables
Variables are classified into categorical and numerical types.
3.1 Categorical Variables (Qualitative)
Categorical variables represent distinct groups or categories.
- Nominal: No order or ranking. (e.g., Colors: {Red, Blue, Green})
- Ordinal: Categories have a meaningful order. (e.g., Education level: {High School, Bachelor’s, Master’s})
3.2 Numerical Variables (Quantitative)
Numerical variables represent measurable quantities.
- Discrete: Can take only specific values, usually integers. (e.g., Number of children: {0, 1, 2, 3})
- Continuous: Can take any value within a range. (e.g., Height: {5.4 ft, 5.5 ft, 6.2 ft})
4. Data Visualization: Histograms and KDE
4.1 Histograms
A histogram is a graphical representation of the frequency distribution of numerical data. It consists of bins, where each bin represents a range of values, and the height of the bar represents the frequency.
🔹 Example of a Histogram:
- If we have test scores {50, 55, 60, 60, 65, 70, 75, 80, 85, 90}, a histogram would show how often scores fall within certain ranges (bins like 50-60, 60-70, etc.).
🔹 Advantages of Histograms: ✅ Shows the distribution of data
✅ Helps detect skewness and outliers
4.2 Kernel Density Estimation (KDE)
A Kernel Density Estimate (KDE) is a smoothed version of a histogram. Instead of using bars, KDE uses a smooth curve to estimate the probability density function of a dataset.
🔹 Why Use KDE?
- Unlike histograms, KDE does not depend on bin width, providing a clearer view of data distribution.
🔹 Example: If we have a dataset of student heights, a KDE plot would give a smooth curve that helps visualize the probability density of different height ranges.
🔹 Difference Between Histogram & KDE
| Feature | Histogram | KDE |
|---|---|---|
| Representation | Binned Bars | Smooth Curve |
| Sensitivity | Depends on bin width | Depends on kernel bandwidth |
| Use Case | Discrete counts | Probability density estimation |
Understanding Percentiles, Quartiles & the 5-Number Summary
The Foundation of Exploratory Data Analysis (EDA)
When you’re trying to understand a dataset or detect outliers, few tools are more powerful and intuitive than percentiles, quartiles, and the 5-number summary. These help you explore how your data is distributed and identify extreme values with precision.
🔢 1. Percentiles
Percentiles divide the dataset into 100 equal parts. Each percentile tells you the value below which a certain percentage of data falls.
Example:
- 25th percentile (P25) → 25% of data lies below this value.
- 90th percentile (P90) → 90% of data lies below this value.
Percentiles help describe the relative standing of a value in the dataset.
🧮 2. Quartiles
Quartiles are specific percentiles that divide your data into four equal parts.
| Quartile | Percentile Equivalent | Meaning |
|---|---|---|
| Q1 (1st Quartile) | 25th Percentile | 25% of data below |
| Q2 (Median) | 50th Percentile | Middle value |
| Q3 (3rd Quartile) | 75th Percentile | 75% of data below |
🧰 3. The 5-Number Summary
The 5-number summary is one of the most important techniques in descriptive statistics. It gives a quick overview of the distribution of your data and is crucial for visualizations like box plots.
✅ It includes:
- Minimum – Smallest value in the dataset
- Q1 (1st Quartile) – 25% of data lies below this
- Median (Q2) – 50% of data lies below this
- Q3 (3rd Quartile) – 75% of data lies below this
- Maximum – Largest value in the dataset
📐 4. Interquartile Range (IQR)
The Interquartile Range (IQR) measures the spread of the middle 50% of the data. IQR=Q3−Q1
This is a robust measure of variability that is not affected by outliers.
🚨 5. Detecting Outliers using IQR
The IQR can be used to create fences beyond which data points are considered outliers.
🔻 Lower Fence:
Lower Fence=Q1−1.5×IQR
🔺 Upper Fence:
Upper Fence=Q3+1.5×IQR
Any value below the lower fence or above the upper fence is typically classified as an outlier.
📊 6. Example: 5-Number Summary + IQR Calculation
📘 Dataset:
data = [7, 8, 8, 10, 12, 13, 14, 15, 16, 22, 40]
🔍 Step-by-Step:
- Minimum = 7
- Maximum = 40
- Median (Q2) = 13
- Q1 (25th percentile) = 9
- Q3 (75th percentile) = 16
So the 5-number summary is:
[Minimum = 7, Q1 = 9, Median = 13, Q3 = 16, Maximum = 40]
📏 Calculate IQR:
IQR=Q3−Q1=16−9=7
🔎 Determine fences:
- Lower Fence = 9−(1.5×7)=9−10.5=−1.59 – (1.5 \times 7) = 9 – 10.5 = -1.59−(1.5×7)=9−10.5=−1.5
- Upper Fence = 16+(1.5×7)=16+10.5=26.516 + (1.5 \times 7) = 16 + 10.5 = 26.516+(1.5×7)=16+10.5=26.5
🧨 Outlier Detection:
Any value > 26.5 or < -1.5 is an outlier.
✅ So, in this dataset, 40 is an outlier.
📦 7. Visual Representation: Box Plot
The 5-number summary is used in box plots to visually summarize data.
- The box spans from Q1 to Q3
- A line marks the median (Q2)
- “Whiskers” extend to the smallest/largest non-outlier values
- Outliers are shown as dots or stars beyond the whiskers
🌟 Why Is This Important?
| Feature | Reason |
|---|---|
| Exploratory Data Analysis (EDA) | Quickly understand the spread and central tendency |
| Outlier Detection | IQR-based fences help detect anomalies |
| Feature Scaling & Normalization | Useful for feature engineering |
| Robust Statistics | Median and IQR are unaffected by extreme values, unlike mean & standard deviation |
📌 Summary Table
| Term | Description | Formula |
|---|---|---|
| Q1 | 25th percentile | – |
| Q2 (Median) | 50th percentile | – |
| Q3 | 75th percentile | – |
| IQR | Interquartile range | Q3−Q1Q3 – Q1Q3−Q1 |
| Lower Fence | Threshold for low outliers | Q1−1.5×IQR |
| Upper Fence | Threshold for high outliers | Q3+1.5×IQR |
| Outliers | Values outside fences | x<LF or x> UF x < LF |
Correlation and Covariance: A Comprehensive Guide
Covariance and correlation are fundamental statistical concepts used to measure the relationship between variables. While they serve similar purposes, they differ in important ways. Let’s explore both concepts in depth.
Covariance
Covariance measures how two variables change together. It indicates the direction of the linear relationship between variables.
Mathematical Definition
The sample covariance formula is:
Cov(X,Y) = Σ[(x_i – x̄)(y_i – ȳ)] / (n-1)
Where:
- x_i and y_i are individual data points
- x̄ and ȳ are the means of X and Y
- n is the number of data pairs
Interpretation
- Positive covariance: Variables tend to move in the same direction
- Negative covariance: Variables tend to move in opposite directions
- Zero covariance: No linear relationship between variables
Example
Let’s consider stock prices for two companies, A and B, over 5 days:
Day | Company A | Company B —-|———–|———- 1 | $10 | $5 2 | $12 | $6 3 | $11 | $4 4 | $13 | $7 5 | $14 | $8Step 1: Calculate means
- Mean of A = (10+12+11+13+14)/5 = $12
- Mean of B = (5+6+4+7+8)/5 = $6
Step 2: Calculate deviations and their products
Day | A-Mean(A) | B-Mean(B) | Product —-|———–|———–|——– 1 | -2 | -1 | 2 2 | 0 | 0 | 0 3 | -1 | -2 | 2 4 | 1 | 1 | 1 5 | 2 | 2 | 4Step 3: Sum products and divide by (n-1) Cov(A,B) = (2+0+2+1+4)/(5-1) = 9/4 = 2.25
The positive covariance indicates that when stock A increases, stock B tends to increase as well.
Types of Covariance
1. Positive Covariance
Indicates that variables tend to move in the same direction.
Example: Height and weight in humans typically have positive covariance because taller people generally weigh more than shorter people.
2. Negative Covariance
Indicates that variables tend to move in opposite directions.
Example: Hours spent studying and number of errors on a test typically have negative covariance because more study time usually results in fewer errors.
3. Zero Covariance
Indicates no linear relationship between variables.
Example: Shoe size and intelligence would likely have zero covariance because there’s no reason one would affect the other.
4. Autocovariance
Measures the covariance of a variable with itself at different time points.
Example: In time series analysis, the price of gold today might have a high autocovariance with its price yesterday.
5. Cross-covariance
Measures the similarity between two different time series at different time lags.
Example: Rainfall amounts and reservoir levels might show cross-covariance with a lag, as it takes time for rainfall to affect reservoir levels.
Correlation
Correlation is a standardized version of covariance that measures both the strength and direction of a linear relationship between variables. It always falls between -1 and 1.
Mathematical Definition
The Pearson correlation coefficient is:
ρ(X,Y) = Cov(X,Y) / (σ_X × σ_Y)
Where:
- Cov(X,Y) is the covariance
- σ_X is the standard deviation of X
- σ_Y is the standard deviation of Y
Interpretation
- Correlation of 1: Perfect positive correlation
- Correlation of -1: Perfect negative correlation
- Correlation of 0: No linear correlation
- Correlation between 0 and 1: Positive correlation
- Correlation between -1 and 0: Negative correlation
Example
Continuing with our stock price example:
Step 1: Calculate standard deviations
- For Company A: σ_A = sqrt([((-2)² + 0² + (-1)² + 1² + 2²)/5]) = sqrt(10/5) = sqrt(2) ≈ 1.41
- For Company B: σ_B = sqrt([((-1)² + 0² + (-2)² + 1² + 2²)/5]) = sqrt(10/5) = sqrt(2) ≈ 1.41
Step 2: Calculate correlation
- ρ(A,B) = Cov(A,B) / (σ_A × σ_B) = 2.25 / (1.41 × 1.41) = 2.25/2 = 1.125
(Note: In practice, correlation should always be between -1 and 1. The slight discrepancy here is due to rounding. The actual correlation would be 1, indicating perfect positive correlation.)
Types of Correlation
1. Pearson Correlation
Measures linear relationships between variables with continuous, normally distributed data.
Example: The relationship between height and weight typically follows a linear pattern suitable for Pearson correlation.
2. Spearman Rank Correlation
Measures monotonic relationships, where variables tend to change together but not necessarily at a constant rate.
Example: The relationship between age and reading ability in children might be monotonic (generally increasing) but not strictly linear.
Pearson Correlation Coefficient and Spearman Rank Correlation Coefficient
Let me explain both correlation methods in detail, including their formulas, interpretations, and when to use each one.
Pearson Correlation Coefficient
The Pearson correlation coefficient (r) measures the linear relationship between two continuous variables. It’s the most commonly used correlation measure in statistics.
Formula
For two variables X and Y with n observations, the Pearson correlation coefficient is calculated as:
r = Σ[(xᵢ – x̄)(yᵢ – ȳ)] / √[Σ(xᵢ – x̄)² × Σ(yᵢ – ȳ)²]
Alternatively, it can be expressed as:
r = Cov(X,Y) / (σₓ × σᵧ)
Where:
- xᵢ and yᵢ are individual data points
- x̄ and ȳ are the means of X and Y
- Cov(X,Y) is the covariance between X and Y
- σₓ and σᵧ are the standard deviations of X and Y
Properties
- Range: Always between -1 and +1
- Interpretation:
- r = 1: Perfect positive linear relationship
- r = -1: Perfect negative linear relationship
- r = 0: No linear relationship
- 0 < |r| < 0.3: Weak correlation
- 0.3 ≤ |r| < 0.7: Moderate correlation
- 0.7 ≤ |r| < 1: Strong correlation
- Symmetry: r(X,Y) = r(Y,X)
- Invariance to linear transformations: If Y = aX + b (where a > 0), then r = 1
Example Calculation
Consider these data points:
CopyX: 1, 2, 3, 4, 5
Y: 2, 3, 5, 7, 11Step 1: Calculate means
- x̄ = (1+2+3+4+5)/5 = 3
- ȳ = (2+3+5+7+11)/5 = 5.6
Step 2: Calculate deviations, squares, and products
X | Y | X-x̄ | Y-ȳ | (X-x̄)² | (Y-ȳ)² | (X-x̄)(Y-ȳ) —–|—–|—–|—–|———|———|———— 1 | 2 | -2 | -3.6| 4 | 12.96 | 7.2 2 | 3 | -1 | -2.6| 1 | 6.76 | 2.6 3 | 5 | 0 | -0.6| 0 | 0.36 | 0 4 | 7 | 1 | 1.4| 1 | 1.96 | 1.4 5 | 11 | 2 | 5.4| 4 | 29.16 | 10.8 —–|—–|—–|—–|———|———|———— Sum: | | | | 10 | 51.2 | 22.0Step 3: Calculate r r = 22.0 / √(10 × 51.2) = 22.0 / √512 = 22.0 / 22.63 ≈ 0.972
This indicates a very strong positive linear relationship between X and Y.
Assumptions and Limitations
- Assumes variables have a linear relationship
- Sensitive to outliers
- Both variables should be normally distributed for hypothesis testing
- Measures only linear relationships
Spearman Rank Correlation Coefficient
The Spearman rank correlation coefficient (ρ or rₛ) measures the monotonic relationship between two variables by using their ranks rather than actual values.
Formula
For two variables X and Y with n observations, the Spearman correlation is calculated as:
ρ = 1 – (6 × Σd²) / (n(n² – 1))
Where:
- d is the difference between the ranks of corresponding values of X and Y
- n is the number of observations
If there are no tied ranks, this simplifies to:
ρ = Pearson correlation coefficient between the ranks of X and Y
Properties
- Range: Always between -1 and +1
- Interpretation:
- ρ = 1: Perfect monotonic increasing relationship
- ρ = -1: Perfect monotonic decreasing relationship
- ρ = 0: No monotonic relationship
- Similar magnitude interpretation as Pearson (weak, moderate, strong)
- Invariant to any monotonic transformation of the variables
- Less sensitive to outliers than Pearson
Example Calculation
Consider these data points:
X: 5, 10, 15, 20, 25
Y: 2, 4, 5, 9, 12Step 1: Rank the values in each variable (1 = lowest, n = highest)
X | Y | Rank X | Rank Y | d (difference) | d² —–|—–|——–|——–|—————-|—– 5 | 2 | 1 | 1 | 0 | 0 10 | 4 | 2 | 2 | 0 | 0 15 | 5 | 3 | 3 | 0 | 0 20 | 9 | 4 | 4 | 0 | 0 25 | 12 | 5 | 5 | 0 | 0 —–|—–|——–|——–|—————-|—– Σd² = 0Step 2: Calculate ρ ρ = 1 – (6 × 0) / (5(5² – 1)) = 1 – 0/120 = 1
This indicates a perfect monotonic relationship between X and Y.
Handling Tied Ranks
When ties occur, each tied value is assigned the average of the ranks they would have received if they were distinct. For example, if the 2nd and 3rd positions are tied, both receive rank 2.5.
For tied ranks, the formula can be adjusted to:
ρ = (Σ(xᵢ – x̄)(yᵢ – ȳ)) / √(Σ(xᵢ – x̄)² × Σ(yᵢ – ȳ)²)
Where xᵢ and yᵢ are now the ranks.
Assumptions and Limitations
- Only assumes variables have a monotonic relationship (not necessarily linear)
- Less powerful than Pearson when data is truly linear and normally distributed
- Computationally more intensive for large datasets
When to Use Each Coefficient
Use Pearson When:
- Data is continuous
- The relationship appears linear
- Both variables are approximately normally distributed
- Outliers are minimal or have been addressed
- You need to measure the strength of strictly linear relationships
Use Spearman When:
- Data is ordinal or ranked
- The relationship appears monotonic but not necessarily linear
- Variables are not normally distributed
- Outliers are present
- You want to capture any monotonic relationship, not just linear ones
- You’re analyzing variables where exact values are less important than relative ordering
Practical Examples
- Pearson Correlation: Relationship between height and weight in a population (typically linear)
- Spearman Correlation: Relationship between customer satisfaction ratings (1-5 scale) and likelihood to repurchase (where the relationship might be monotonic but not strictly linear)
Key Differences Between Covariance and Correlation
- Scale: Covariance is affected by the scale of the variables; correlation is standardized between -1 and 1.
- Units: Covariance has units (product of the units of the two variables); correlation is unitless.
- Comparability: Correlations can be compared across different datasets; covariances generally cannot.
- Interpretation: Correlation provides both direction and strength; covariance only reliably indicates direction.
Applications in Data Analysis
Portfolio Management
- Positive covariance between assets increases portfolio risk
- Negative covariance helps diversify risk
Machine Learning
- Correlation analysis helps identify relevant features
- Principal Component Analysis uses covariance matrices to reduce dimensionality
Quality Control
- Correlation between process variables helps identify root causes of defects
Economic Analysis
- Correlation between GDP and unemployment rate helps understand economic cycles
Probability Distribution
The Relationship Between PDF, PMF, and CDF
Probability Mass Function (PMF)
The PMF applies to discrete random variables and gives the probability that a random variable X equals a specific value x.
Mathematical Definition: P(X = x) = PMF(x)
Properties:
- Non-negative: PMF(x) ≥ 0 for all x
- Sum to 1: Σ PMF(x) = 1 (over all possible values)
- Range: 0 ≤ PMF(x) ≤ 1
Example: For a fair six-sided die, the PMF is:
- P(X = 1) = P(X = 2) = … = P(X = 6) = 1/6
Probability Density Function (PDF)
The PDF applies to continuous random variables and represents the relative likelihood of the random variable taking on a specific value.
Mathematical Definition: f(x) = dF(x)/dx, where F(x) is the CDF
Properties:
- Non-negative: f(x) ≥ 0 for all x
- Area equals 1: ∫f(x)dx = 1 (integrated over all possible values)
- P(a ≤ X ≤ b) = ∫(from a to b) f(x)dx
- Unlike PMF, PDF can exceed 1 at specific points
Example: The PDF of a standard normal distribution is: f(x) = (1/√(2π)) * e^(-x²/2)
Cumulative Distribution Function (CDF)
The CDF applies to both discrete and continuous random variables and gives the probability that X is less than or equal to x.
Mathematical Definition: F(x) = P(X ≤ x)
For discrete variables: F(x) = Σ PMF(t) for all t ≤ x For continuous variables: F(x) = ∫(from -∞ to x) f(t)dt
Properties:
- Non-decreasing: F(x₁) ≤ F(x₂) if x₁ < x₂
- Limits: lim(x→-∞) F(x) = 0 and lim(x→∞) F(x) = 1
- Range: 0 ≤ F(x) ≤ 1
- P(a < X ≤ b) = F(b) – F(a)
Example: For a standard normal distribution, the CDF doesn’t have a simple closed form but is often denoted as Φ(x).
Types of Probability Distributions
Probability distributions come in two main categories:
Discrete Probability Distributions
- Bernoulli Distribution: Models binary outcomes (success/failure)
- Binomial Distribution: Sum of independent Bernoulli trials
- Poisson Distribution: Models rare events in fixed intervals
- Geometric Distribution: Number of trials until first success
- Negative Binomial: Number of trials until k successes
- Hypergeometric: Sampling without replacement
- Discrete Uniform: Equal probability for all outcomes
Continuous Probability Distributions
- Normal/Gaussian Distribution: Bell-shaped curve
- Standard Normal Distribution: Normal with μ=0, σ=1
- Uniform Distribution: Equal probability density over interval
- Exponential Distribution: Time between Poisson events
- Log-Normal Distribution: When logarithm follows normal distribution
- Chi-Square Distribution: Sum of squared standard normal variables
- Student’s t-Distribution: Used for small sample statistics
- F-Distribution: Ratio of chi-squared distributions
- Beta Distribution: Models probabilities or proportions
- Gamma Distribution: Generalizes exponential and chi-squared
- Weibull Distribution: Models failure rates and reliability
- Pareto Distribution: Power-law probability distribution
- Cauchy Distribution: Heavy-tailed distribution
Bernoulli Distribution
The Bernoulli distribution is the simplest discrete probability distribution, modeling a single binary outcome.
Properties
- PMF: P(X = x) = p^x × (1-p)^(1-x) for x ∈ {0, 1}
- Mean: E[X] = p
- Variance: Var(X) = p(1-p)
- Parameter: p = probability of success (0 ≤ p ≤ 1)
Example
Flipping a coin once with p = 0.5 probability of heads:
- P(X = 1) = 0.5 (heads)
- P(X = 0) = 0.5 (tails)
Bernoulli Distribution
Image
Applications
- Quality control (defective/non-defective)
- Medical tests (positive/negative)
- Elections (win/lose)
- Any yes/no, success/failure scenario
Binomial Distribution
The binomial distribution models the number of successes in a fixed number of independent Bernoulli trials.
Properties
- PMF: P(X = k) = (n choose k) × p^k × (1-p)^(n-k)
- Mean: E[X] = np
- Variance: Var(X) = np(1-p)
- Parameters:
- n = number of trials
- p = probability of success on each trial
Example
Flipping a fair coin 10 times and counting heads:
- n = 10, p = 0.5
- P(X = 5) = (10 choose 5) × 0.5^5 × 0.5^5 = 252 × 0.001953 = 0.246
Binomial Distribution
Image
Applications
- Quality control (number of defects in a batch)
- Medical studies (number of patients recovering)
- Sports statistics (number of successful shots)
- Election polling (number of voters supporting a candidate)
Poisson Distribution
The Poisson distribution models the number of events occurring in a fixed interval of time or space, when these events happen at a constant average rate.
Properties
- PMF: P(X = k) = (e^(-λ) × λ^k) / k!
- Mean: E[X] = λ
- Variance: Var(X) = λ
- Parameter: λ = average number of events per interval
Example
If emails arrive at an average rate of 5 per hour:
- λ = 5
- P(X = 3) = (e^(-5) × 5^3) / 3! = (0.0067 × 125) / 6 = 0.140
Poisson Distribution
Image
Applications
- Customer arrivals at a service counter
- Number of calls to a call center
- Number of defects in manufacturing
- Number of accidents at an intersection
- Radioactive decay events
Normal/Gaussian Distribution
The normal distribution is the most important continuous probability distribution, characterized by its bell-shaped curve.
Properties
- PDF: f(x) = (1/(σ√(2π))) × e^(-(x-μ)²/(2σ²))
- Mean: E[X] = μ
- Variance: Var(X) = σ²
- Parameters:
- μ = mean (location parameter)
- σ = standard deviation (scale parameter)
Example
Human heights often follow a normal distribution. If adult male heights have μ = 175 cm and σ = 7 cm:
- 68% of men have heights between 168-182 cm (μ ± σ)
- 95% of men have heights between 161-189 cm (μ ± 2σ)
- 99.7% of men have heights between 154-196 cm (μ ± 3σ)
Tools
Testimonial

Nevine Acotanza test
Chief Operating OfficerAndroid App Development
via Upwork - Mar 4, 2015 - Aug 30, 2021 testMaecenas finibus nec sem ut imperdiet. Ut tincidunt est ac dolor aliquam sodales. Phasellus sed mauris hendrerit, laoreet sem in, lobortis mauris hendrerit ante. Ut tincidunt est ac dolor aliquam sodales phasellus smauris

Jone Duone Joe
Operating OfficerWeb App Development
Upwork - Mar 4, 2016 - Aug 30, 2021Maecenas finibus nec sem ut imperdiet. Ut tincidunt est ac dolor aliquam sodales. Phasellus sed mauris hendrerit, laoreet sem in, lobortis mauris hendrerit ante. Ut tincidunt est ac dolor aliquam sodales phasellus smauris

Nevine Dhawan
Operating OfficerAndroid App Design
Fiver - Mar 4, 2015 - Aug 30, 2021Maecenas finibus nec sem ut imperdiet. Ut tincidunt est ac dolor aliquam sodales. Phasellus sed mauris hendrerit, laoreet sem in, lobortis mauris hendrerit ante. Ut tincidunt est ac dolor aliquam sodales phasellus smauris
My Pricing
Make Your Single Page
Elementor / WPBakeryAll the Lorem Ipsum generators on the Internet tend to repeat predefined chunks as necessary
1 Page with Elementor
Design Customization
Responsive Design
Content Upload
Design Customization
2 Plugins/Extensions
Multipage Elementor
Design Figma
MAintaine Design
Content Upload
Design With XD
8 Plugins/Extensions
Make Your Single Page
Elementor / WPBakeryAll the Lorem Ipsum generators on the Internet tend to repeat predefined chunks as necessary
1 Page with Elementor
Design Customization
Responsive Design
Content Upload
Design Customization
2 Plugins/Extensions
Multipage Elementor
Design Figma
MAintaine Design
Content Upload
Design With XD
8 Plugins/Extensions
Make Your Single Page
Elementor / WPBakeryAll the Lorem Ipsum generators on the Internet tend to repeat predefined chunks as necessary
1 Page with Elementor
Design Customization
Responsive Design
Content Upload
Design Customization
2 Plugins/Extensions
Multipage Elementor
Design Figma
MAintaine Design
Content Upload
Design With XD
8 Plugins/Extensions
Contact With Me

Tejas Kamble
AI EngineerPython, AI-ML, NLP Developer and researcher, I am available for freelance work. Connect with me via and call in to my account.
Phone: +917666215102 Mail: [email protected]